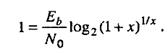Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Компромиссы при использовании модуляции и кодированияСодержание книги Поиск на нашем сайте
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика М.Ф. Решетнева
Кафедра ЭТТ Реферат Компромиссы при использовании модуляции и кодирования Выполнил: Студент гр. Е-62 Гречаник К.А.
Проверил: профессор Сивирин П.Я.
Красноярск 2010
Содержание Введение 3 1. Немного о требованиях к каналу связи 4 2. Компромиссы при использовании модуляции и кодирования 11 Заключение 21 Список литературы 22
Введение Системные компромиссы ‑ это неотъемлемая часть всех разработок цифровых систем связи. Разработчик должен стремиться к 1) увеличению скорости передачи бит R до максимально возможной; 2) минимизации вероятности появления битовой ошибки РB, 3) минимизации потребляемой мощности, или, что то же самое, минимизации требуемого отношения энергии одного бита к спектральной плотности мощности шума Еb/Nо; 4) минимизации ширины полосы пропускания W, 5) максимизации эффективности использования системы, т.е. к обеспечению надежного обслуживания для максимального числа пользователей с минимальными задержками и максимальной устойчивостью к возникновению конфликтов; и 6) минимизации конструктивной сложности системы, вычислительной нагрузки и стоимости системы. Конечно, разработчик системы может попытаться удовлетворить всем требованиям одновременно. Однако очевидно, что требования 1 и 2 противоречат требованиям 3 и 4; они предусматривают одновременное увеличение скорости R и минимизацию РB, Еb/Mо, W. Существует несколько сдерживающих факторов и теоретических ограничений, которые неизбежно влекут за собой компромиссы в любых системных требованиях: ‑Минимальная теоретически требуемая ширина полосы частот по Найквисту ‑Теорема о пропускной способности Шеннона-Хартли (и предел Шеннона) ‑Государственное регулирование (например, распределение частот) ‑Технологические ограничения (например, современные комплектующие)
‑Другие системные требования (например, орбиты спутников) 1. Немного о требованиях к каналу связи
Предел Шеннона
Существует нижнее предельное значение Еb/Nо, при котором ни при какой скорости передачи нельзя осуществить безошибочную передачу информации. С помощью соотношения
Пусть
Тогда
При C/W→0
В децибелах Еb/Nо= ‑1,6дБ. Это значение Еb/Nо называется пределом Шеннона. На рис. 1, а предел Шеннона ‑ это кривая зависимости РB от Еb/Nо при k→∞. При Еb/Nо= ‑1,6дБ. данная кривая скачкообразно изменяет свое значение от Рв ~ 1/2 на Рв = 0. В действительности достичь предела Шеннона невозможно, поскольку k возрастает неограниченно, а с ростом к возрастают требования к полосе пропускания и повышается сложность реализации системы. Работа Шеннона ‑ это теоретическое доказательство существования кодов, которые могут улучшить Рв или снизить требуемое значение Еb/Nо от уровней некодированных двоичных схем модуляции до уровней, приближающихся к предельной кривой. При вероятности появления битовой ошибки 10-5 двоичная фазовая манипуляция (BPSK) требует значения Еb/Nо, равного 9,6 дБ (оптимум некодированной двоичной модуляции). Следовательно, за счет использования кодирования, производительность можно повысить на 11,2 дБ по сравнению с некодированной двоичной модуляцией. Оптимальную разработку системы можно наилучшим образом представить как поиск рациональных компромиссов среди различных ограничений и взаимно противоречивых требований. Компромиссы модуляции и кодирования, т.е. выбор конкретных схем модуляции и кодирования для наилучшего использования переданной мощности и ширины полосы, являются очень важными, поскольку имеется много причин для снижения мощности, а также существует необходимость экономии спектра радиочастот.
Энтропия Для разработки системы связи с определенной способностью к обработке сообщений нужна метрика измерения объема передаваемой информации. Шеннон ввел такую метрику H, называемую энтропией источника сообщений (имеющего n возможных выходных значений). Энтропия определяется как среднее количество информации, приходящееся на один выход источника, и выражается следующим образом:
бит/выход источника. Здесь рi вероятность i-того выходного значения и Σрi=1. Если сообщение двоичное или источник имеет только два возможных выходных значения с вероятностями р и q=(1-р), выражение для энтропии примет следующий вид:
Неоднозначность и эффективная скорость передачи информации Пусть по двоичному симметричному каналу со скоростью 1000 двоичных символов/с происходит передача информации, а априорная вероятность передачи нуля или единицы одинакова. Допустим также, что, вероятность приема единицы равна 1/2 (то же самое ‑ для нуля). В таком случае половина принятых символов должна случайно оказаться правильной, и может создаться впечатление, что система обеспечивает скорость 500 бит/с, хотя на самом деле никакой информации не передается. Одинаково "хороший" прием дает и использование "информации", поступившей из канала, и генерация этой "информации" методом подбрасывания правильной монеты. Утраченной является информация о корректности переданных символов. Для оценки неопределенности в принятом сигнале Шеннон использует поправочный коэффициент, который называет неоднозначностью. Неоднозначность определяется как условная энтропия сообщения X, обусловленная данным сообщением Y, или
где X сообщение, переданное источником, Y ‑ принятый сигнал, Р(Х, У) ‑ совместная вероятность X и Y, а Р{Х|У) ‑ условная вероятность X при приеме Y. Неоднозначность можно представить как неуверенность в передаче X при условии принятия Y. Для канала без ошибок Н{Х|У)=0, поскольку принятие сообщения Y абсолютно точно определяет X. Для канала с ненулевой вероятностью возникновения символьной ошибки Н{Х|У)>0, поскольку канал вносит некоторую неопределенность. Шеннон показал, что среднее эффективное количество информации Heff в приемнике получается путем вычитания неоднозначности из энтропии источника. Следовательно,
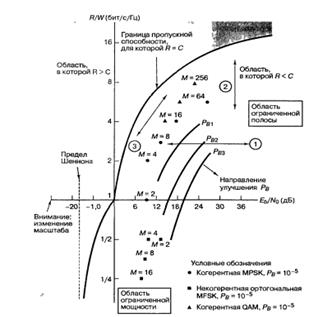
Плоскость "полоса-эффективность.
Рис. 3. Плоскость полоса-эффективность. С помощью уравнения (1) можно составить график зависимости нормированной полосы пропускания канала W/C (в Гц/бит/с) от Еb/Nо. Можно показать, что качественно спроектированные системы должны стремиться к работе в области излома кривой компромисса между полосой пропускания и мощностью для идеального (R=С) канала. Характеристики реальных систем часто отличаются от идеальных не более чем на 10 дБ. Наличие излома означает, что в системах, в которых предпринимается попытка уменьшить занимаемую полосу пропускания канала или снизить требуемую мощность, приходится все больше повышать значение другого параметра (что является не очень желательным). Назовем плоскость зависимости C/W от Еb/Nо плоскостью "полоса-эффективность". Ордината R/W ‑ это мера объема данных, которые можно передать через единицу полосы частот за данное время; следовательно, она отображает эффективность использования ресурса полосы пропускания. Независимая переменная Еb/Nо измеряется в децибелах. Кривая R=С ‑это граница, разделяющая область реальных прикладных систем связи и область, в которой такие системы связи теоретически невозможны. Характеристика эффективности полосы пропускания на рис. 3 устанавливает предельные параметры, которые достижимы для прикладных систем. Отметим, что на рис. 3 проиллюстрирована зависимость эффективности использования полосы частот от Еb/Nо для систем с одной несущей. Для систем с множественными несущими эффективность использования полосы частот зависит от разнесения несущих (и типа модуляции). В этом случае компромисс ‑ это насколько разнесены несущие (что приводит к повышению эффективности использования полосы частот) без возникновения неприемлемых помех соседних каналов.
Заключение В данном реферате рассмотрены основные задачи разработки системы: получение максимальной скорости передачи информации при одновременном снижении вероятности возникновения ошибки и значения Еb/Nо, сужении полосы пропускания и уменьшении сложности. Компромиссы были изучены эвристически в двух плоскостях: вероятность появления ошибки и эффективность использования полосы частот. Первая явно иллюстрирует компромисс между Еb/Nо и РВ, а также неявно отображает расход полосы пропускания. На второй показан компромисс между R/W и Еb/Nо при неявном изображении поведения РВ. Кроме того, описаны типичные шаги, которые предпринимаются при удовлетворении требований к полосе пропускания, мощности и вероятности появления ошибок в системе цифровой связи. Также рассмотрены некоторые ограничения, которые делают невозможным неограниченное повышение производительности. Согласно критерию Найквиста, полосу пропускания нельзя сужать бесконечно. Существует теоретический предел; для передачи RSсимволов/с без межсимвольной интерференции нужно задействовать, как минимум, RS/2 Гц полосы пропускания. Теорема Шеннона-Хартли связана с компромиссом между мощностью и полосой пропускания, а также определяет другое важное ограничение ‑ предел Шеннона. Предел Шеннона, равный -1,6 дБ, ‑это минимальное теоретически возможное значение которое (совместно с канальным кодированием) необходимо для получения сколь угодно низкой вероятности возникновения ошибки в канале c аддитивным гауссовским шумом. Более общим ограничением является значение пропускной способности канала, превышение которой автоматически запрещает безошибочную передачу сигналов. Приведены некоторые схемы модуляции с эффективным использованием полосы пропускания, такие как манипуляция с минимальным сдвигом (MSK) и квадратурная амплитудная модуляция (QAM).
Список литературы 1. Цифровая связь. Теоретические основы и практическое применение. Изд. 2, испр.: Пер. с англ. – М.: Издательский дом «Вильямс», 2003г.‑1104с.
2. Учебное пособие: Космические и наземные системы радиосвязи. П.Я. Сивирин.
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика М.Ф. Решетнева
Кафедра ЭТТ Реферат Компромиссы при использовании модуляции и кодирования Выполнил: Студент гр. Е-62 Гречаник К.А.
Проверил: профессор Сивирин П.Я.
Красноярск 2010
Содержание Введение 3 1. Немного о требованиях к каналу связи 4 2. Компромиссы при использовании модуляции и кодирования 11 Заключение 21 Список литературы 22
Введение Системные компромиссы ‑ это неотъемлемая часть всех разработок цифровых систем связи. Разработчик должен стремиться к 1) увеличению скорости передачи бит R до максимально возможной; 2) минимизации вероятности появления битовой ошибки РB, 3) минимизации потребляемой мощности, или, что то же самое, минимизации требуемого отношения энергии одного бита к спектральной плотности мощности шума Еb/Nо; 4) минимизации ширины полосы пропускания W, 5) максимизации эффективности использования системы, т.е. к обеспечению надежного обслуживания для максимального числа пользователей с минимальными задержками и максимальной устойчивостью к возникновению конфликтов; и 6) минимизации конструктивной сложности системы, вычислительной нагрузки и стоимости системы. Конечно, разработчик системы может попытаться удовлетворить всем требованиям одновременно. Однако очевидно, что требования 1 и 2 противоречат требованиям 3 и 4; они предусматривают одновременное увеличение скорости R и минимизацию РB, Еb/Mо, W. Существует несколько сдерживающих факторов и теоретических ограничений, которые неизбежно влекут за собой компромиссы в любых системных требованиях: ‑Минимальная теоретически требуемая ширина полосы частот по Найквисту ‑Теорема о пропускной способности Шеннона-Хартли (и предел Шеннона) ‑Государственное регулирование (например, распределение частот) ‑Технологические ограничения (например, современные комплектующие) ‑Другие системные требования (например, орбиты спутников) 1. Немного о требованиях к каналу связи
|
||||||||
|
Последнее изменение этой страницы: 2020-03-02; просмотров: 128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.172.105 (0.01 с.) |


 можно рассчитать предельное значение.
можно рассчитать предельное значение.
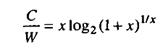 (1)
(1)