
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение касательных напряжений
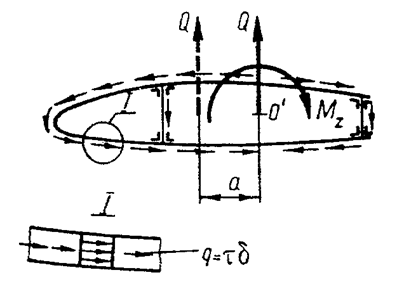
Основные допущения. Касательные напряжения возникают в обшивке и стенках лонжеронов от действия поперечной силы и крутящего момента. При определении касательных напряжений τ исходят из общепринятых допущений теории тонкостенных стержней и оболочек, а именно: принимают, что напряжения τ по толщине обшивки не изменяются, а погонные касательные усилия q = τσ в любой точке сечения направлены по касательной к средней линии сечения контура (рис. 16). Кроме того, считают, что поперечные сечения крыла при кручении могут свободно депланировать, т. е. искажаться в направлении длины оболочки.
Рис. 16
Вначале будем считать, что крыло цилиндрическое. Влияние конусности крыла на величины касательных усилий учтем отдельно. Расчет проведем, не отделяя изгиб от кручения, заменив поперечную силу Q и момент Мz относительно оси z эквивалентной им силой Q, приложенной в точке, находящейся на расстоянии Касательные усилия q в замкнутом контуре (рис. 17) от действия силы Q могут быть определены по формуле
где
fi - площадь элемента, работающего на нормальные напряжения; q п — постоянный поток касательных усилий (рис. 17, б), обеспечивающий равновесие всех сил, действующих в сечении.
Рис. 17.
Сумма моментов сил, действующих в сечении, относительно произвольного полюса О ' должна быть равна нулю:
откуда
Здесь a - расстояние от линии действия силы Q до полюса О '; r - расстояние от полюса до касательной к элементу длины ds контура; В случае многозамкнутого контура расчет основной системы от внешней нагрузки производят подобным образом. При этом статическую неопределимость системы раскрывают, используя известные методы строительной механики, например, метод сил.
Приближенные методы определения касательных напряжений
Помимо допущений, сделанных в предыдущем разделе, ниже будем также пренебрегать работой обшивки на сдвиг от поперечной силы, полагая, что эта сила воспринимается только стенками лонжеронов. Такое допущение не ведет к большой погрешности, поскольку обшивка воспринимает не более 5 — 10% поперечной силы крыла.
Порядок определения касательных усилий рассмотрим на примере расчета двухконтурного сечения крыла (рис. 18). Если контуров три и более, метод расчета остается таким же, несколько усложняются лишь выкладки. Распределение поперечной силы крыла Q между стенками лонжеронов производят пропорционально их жесткостям при изгибе: Это соотношение получается из условия равенства прогибов лонжеронов, нагруженных соответственно силами Q 1 и Q 2. Так как Q 1 + Q 2 = Q, то
Здесь Q i — поперечная сила i -го лонжерона; (EJ) i — жесткость при изгибе i -го лонжерона. Крутящий момент М кр в сечении подсчитывают как момент внешней нагрузки, действующей в сечении, относительно центра жесткости. В рассматриваемом случае (рис. 18, а) центр жесткости (ЦЖ) лежит на линии действия равнодействующей сил Q 1 и Q 2 (на рис. 18 крутящий момент обозначен М к). Координату центра жесткости можно определить, например, по формуле
Рис. 18
Таким образом, крутящий момент в сечении крыла
где d — расстояние от линии действия силы Q до центра жесткости сечения. Крутящий момент в сечении можно определить также как сумму моментов всех внешних и внутренних сил, действующих в сечении, относительно произвольной точки. Например, приняв за полюс точку O (рис. 18, а), найдем:
На рис. 18, а показан момент М кр, уравновешивающий крутящий момент Qd. Распределение крутящего момента между контурами производят пропорционально их жесткостям при кручении. Если в крыле два контура, то из условия равенства относительных углов закручивания контуров имеем:
Из условия равновесия следует, что М кр1 + М кр2 = М кр. Отсюда
где М кр i – крутящий момент i –го контура сечения (рис. 18, б);
Fi – площадь, ограниченная контуром сечения; d - толщина обшивки; dS – элемент длины контура; G – модуль сдвига.
Интегрирование осуществляется по всему контуру. Если в контуре в пределах панели толщина обшивки не изменяется, то
где li и d i длина панели в сечении и толщина стенки. Стрингеры увеличивают жесткость крыла при кручении. Учитывают это, вводя в расчет приведенную толщину обшивки. Для стрингера закрытого сечения, а также открытого, но прикрепленного к обшивке двумя рядами заклепок, приведенная толщина обшивки на участке между заклепками
где b – расстояние вдоль контура между заклепками крепления стрингера к обшивке; D si и d i - длина i –го элемента стрингера (в его сечении) и толщина. Суммирование в формуле для d выполняется по всем элементам стрингера между заклепками крепления его к обшивке.
Фюзеляж
4.1 Назначение фюзеляжа и
Основное назначение фюзеляжа - это размещение экипажа, оборудования, грузопассажиров в соответствии с ТТ. Часто в фюзеляже размещается двигательная установка. Фюзеляж связывает основные части самолета в единое целое: с ним соединяются крыло, оперение, передняя или хвостовая, а иногда и главные опоры шасси, и двигатели. Из многочисленных требований к фюзеляжу можно выделить четыре основные группы: аэродинамические, прочностные, компоновочные и эксплуатационные. Аэродинамические требования определяют внешние очертания, размеры и параметры фюзеляжа, обеспечивающие его минимальное сопротивление в полете и достаточную продольную и путевую устойчивость самолета. Прочностные требования - необходимая прочность, жесткость, долговечность и живучесть конструкции - должны выполняться при минимальном весе фюзеляжа. Указанные требования реализуются приданием фюзеляжу соответствующих внешних обводов. Например, у большинства ЛА фюзеляж имеет круговую форму поперечных сечений, которая выгодна как с аэродинамической, так и с конструктивной точек зрения.
|
||||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 1136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.107.96 (0.009 с.) |
 от точки О ' (рис. 16).
от точки О ' (рис. 16). ,
, - касательные силы изгиба, найденные в предположении, что в некоторой точке n контур разомкнут (рис. 17, б);
- касательные силы изгиба, найденные в предположении, что в некоторой точке n контур разомкнут (рис. 17, б); - статический момент редуцированной площади сечения относительно центральной оси, отсчитываемый от точки n;
- статический момент редуцированной площади сечения относительно центральной оси, отсчитываемый от точки n;
 ,
, .
. - удвоенная площадь, ограниченная контуром.
- удвоенная площадь, ограниченная контуром. .
. .
.
 ,
,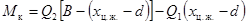 .
.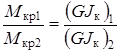 .
. ,
, - жесткость при кручении i -го контура сечения;
- жесткость при кручении i -го контура сечения; ,
, ,
,


