
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение нормальных напряжений
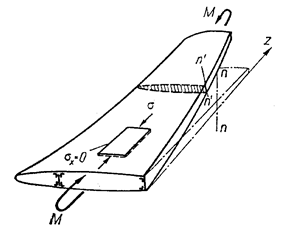
Основные допущения. Современные методы определения нормальных напряжений в крыле основаны на представлении крыла в виде тонкостенной балки. Как и в случае балки, расчет нормальных напряжений в сечении крыла производят при следующих допущениях: 1) плоские сечения n — n (рис. 11), нормальные к оси z крыла, поворачиваясь при деформации, остаются плоскими (n ΄— n ΄); 2) в продольных сечениях панелей крыла нормальные напряжения σ х = 0 (рис. 11); 3) крыло рассматривается как безмоментная тонкостенная оболочка. Первые два допущения обосновываются наличием в крыле часто расположенных нервюр, которые, соединяя различные элементы крыла, обеспечивают его работу как единого целого. Благодаря большой жесткости нервюр в своей плоскости, контур поперечного сечения крыла не деформируется при изгибе. Поэтому можно считать, что сжатие (растяжение) элементов продольного набора крыла не сопровождается поперечными деформациями этих элементов и напряжения σ х = 0.
Рис. 11. Возможность рассматривать крыло как безмоментную оболочку обусловлена тем, что местная жесткость при изгибе отдельных его элементов весьма мала по сравнению с жесткостью при изгибе всего сечения. Ниже излагается расчет сечения крыла от изгибающего момента, действующего в плоскости, перпендикулярной к плоскости хорд. Изгибающий момент, действующий в плоскости хорд, воспринимается, в основном, изгибом верхней и нижней панелей крыла. Нормальные напряжения при этом определяются так же, как и при вертикальном изгибе. По величине они получаются небольшими.
Рис. 12.
Рис. 13.
Исходные данные: изгибающий момент М изг в сечении крыла, геометрические характеристики сечения (рис. 12) и характеристики жесткости элементов продольного набора. Последние задаются в виде зависимостей напряжений σ от деформаций ε (рис. 13). Различные элементы крыла обычно имеют неодинаковые и к тому же нелинейные зависимости σ от ε. Причиной этого может быть различие в материалах, из которых выполнены элементы конструкции, работа отдельных элементов за пределом пропорциональности и после потери устойчивости, а также неодинаковый нагрев их. Метод расчета. Неодинаковое для различных элементов крыла течение кривых σ от ε требует вводить редукционные коэффициенты при определении напряжений, а нелинейный характер этих зависимостей приводит к необходимости определять их в общем случае методом последовательных приближений, или, как его еще принято называть, методом редукционных коэффициентов.
Сущность метода состоит в следующем. Определяя нормальные напряжения, действительное сечение крыла (рис. 12, а) заменяют приведенным (редуцированным) сечением (рис. 12, б), все элементы которого работают по одной фиктивной идеально упругой диаграмме σ - ε (рис. 13). Наклон последней можно назначить произвольно. При этой замене требуют, чтобы усилия S = σ f и S φ = σφ f φ в соответствующих элементах действительного и редуцированного сечений при равных деформациях этих элементов были одинаковыми. Естественно, напряжения элементов действительного и редуцированного сечений будут различными (σ ≠ σφ). Из условия S = S φ получаем:
Отсюда делаем заключение, что площадь f φ сечения элемента редуцированного сечения крыла отличается от площади f соответствующего элемента действительного сечения в отношении φ. Коэффициент
называется редукционным коэффициентом. Нормальные напряжения в редуцированном сечении изменяются по высоте линейно (рис. 12, б) и поэтому могут быть определены по формуле
Истинные значения напряжений в элементах сечения
Здесь М изг — изгибающий момент в сечении; у — координата, отсчитываемая от нейтральной оси редуцированного сечения до рассматриваемого элемента;
При подсчете J φ за нейтральную ось можно принимать ось, параллельную хорде крыла и проходящую через центр тяжести редуцированного сечения. Ошибка за счет пренебрежения поворотом осей получается, как правило, небольшой.
Приближенный метод определения нормальных напряжений Моноблочное крыло. Продольные элементы носка и хвостика крыла расположены сравнительно близко от нейтральной оси. Поэтому в приближенных расчетах работой этих частей контура крыла на нормальные напряжения можно пренебречь. Дальнейшее упрощение получают, заменив оставшееся сечение прямоугольным (рис. 14) с высотой
где F — площадь, ограниченная контуром, образованным обшивкой и стенками лонжеронов; В — расстояние между стенками лонжеронов; H 1, H 2 — соответственно высота переднего и заднего лонжерона.
Для принятой расчетной схемы нормальные напряжения в элементах сечения
Здесь f п, f стр — площадь сечения пояса и стрингера соответственно; n — число стрингеров в панели;
jп, jстр — редукционные коэффициенты пояса и стрингера. При подсчете площади редуцированного сечения Формула может быть выведена и непосредственно из элементарных соображений: сила, действующая в панели, равна моменту, деленному на среднюю высоту сечения крыла; напряжение в элементе равно силе, деленной на редуцированную площадь панели и умноженной на соответствующий редукционный коэффициент. Для конструкций, у которых с ростом нагрузки напряжения в элементах панели сохраняются примерно постоянными вплоть до разрушения наиболее прочного элемента крыла, значения редукционных коэффициентов можно определить по формулам
где σразр.стр и σразр.п — разрушающее напряжение стрингера и пояса соответственно. Конструкции с весьма жесткими стрингерами разрушаются при разрушении стрингера. После потери устойчивости стрингера нагрузка, которую он может держать, резко падает. При этом рост напряжений и разрушение поясов происходят без увеличения внешней нагрузки. В таких конструкциях для сжатой зоны следует принимать φп = φстр = 1 Лонжеронное крыло. При расчете лонжеронного крыла удобнее, особенно если разница в высотах лонжеронов велика, вначале распределить изгибающий момент крыла между лонжеронами, а затем уже определять в них напряжения. Изгибающий момент М изграспределяют между лонжеронами пропорционально их жесткостям при изгибе (рис. 15):
Так как М изг1 + М изг2 = М изг, то Здесь (EJ) i - жесткость при изгибе i -го лонжерона.
Рис. 15. Распределение изгибающего момента крыла между лонжеронами. Соотношение получается из условия равенства углов поворота сечений лонжеронов крыла при изгибе (закон плоских сечений).
|
||||||
|
Последнее изменение этой страницы: 2019-05-20; просмотров: 729; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.2.15 (0.01 с.) |




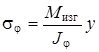 .
. .
. — момент инерции редуцированного сечения.
— момент инерции редуцированного сечения.

 Рис. 14
Рис. 14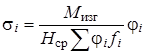
 ,
, — редукционный коэффициент обшивки;
— редукционный коэффициент обшивки; растянутой зоны необходимо учитывать ослабление поясов, стрингеров и обшивки за счет отверстий под болты и заклепки, т. е. под fi следует понимать площадь сечения за вычетом площади, занятой отверстиями под болты и заклепки. В расчете сжатой зоны этого делать не нужно, так как здесь нагрузка передается через стержни болтов и заклепок.
растянутой зоны необходимо учитывать ослабление поясов, стрингеров и обшивки за счет отверстий под болты и заклепки, т. е. под fi следует понимать площадь сечения за вычетом площади, занятой отверстиями под болты и заклепки. В расчете сжатой зоны этого делать не нужно, так как здесь нагрузка передается через стержни болтов и заклепок.
 .
. .
.



