Паразитная связь через общее сопротивление

Представим (рисунок 8.1), что источник наводимого комплексного напряжения Е_н через комплексное сопротивление z_общ, которое входит в цепь приемника наводимого напряжения.

Рис.8.1.Схема паразитной связи через общее сопротивление.

 

Тогда напряжение, наведенное в цепи приемника, будет

(8.1)

Обычно z_н >> z_общ, и пренебрегая z_общ в знаменателе, получаем

Отсюда следует, что при наличии z_общ, входящего как в цепь приемника, так и цепь источника, последним в цепи приемника наводится часть напряжения источника наводки, равная

.

 

Связь через общее сопротивление является наиболее распространенной связью. Примером является связь через внутреннее сопротивление и соедининительные провода источников питания и схем управления работой радиоустройства. Такая связь получается по схеме рис. 8.2. Здесь через цепь источника питания протекают токи всех частот, составляющие спектр сигнала источника наводки. Эти токи дают падение напряжения на всех сопротивлениях, включенных в цепь питания. Часть этих сопротивлений z_общ оказывается включенной в цепи приемника наводки, и напряжение U_н, снимаемое с z_общ, является наводимым напряжением. Величина сопротивления z_общ зависит от частоты наводимого напряжения.

 

Рис.8.2.Паразитная связь через внутреннее сопротивление источника питания или схем управления.

 

Для низких частот – это в основном активное сопротивление соединительных проводов и емкостное сопротивление выходного конденсатора фильтра питания.

Для высоких частот – это в основном сопротивление индуктивностей соединительных проводов и конденсаторов фильтра питания. Индуктивности проводов и распределенные емкости монтажа могут образовывать резонансные контуры.

К этому же виду паразитной связи относится (рис. 8.3) связь через общие отрезки проводов и общие участки корпуса прибора, по которому протекают блуждающие токи.

Рис.8.3.Виды паразитных связей:

а) – через общий лепесток; б) – через общий участок корпуса.

 

Особенно опасно использование присоединенного к корпусу провода, по которому протекает значительный ток I от какого-либо источника, для присоединения других элементов схемы к корпусу. В этом случае величина наводимого напряжения U_н может оказаться значительной, несмотря на небольшое сопротивление общего участка провода (рис. 8.4.)

 

 

 

Рис.8.4.Наводка через общий провод присоединения к корпусу

 

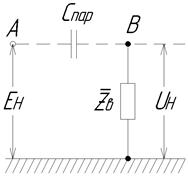
Паразитная емкостная связь

В реальной конструкции любого радиотехнического устройства всегда имеется металлический корпус, или шасси, к которому присоединены некоторые точки схемы прибора непосредственно или через блокировочный конденсатор.

Пусть (рис. 8.5.) напряжение в некоторой точке А равно величине Е_н относительно корпуса, тогда в точке В возникает наведенное напряжение U_н, если последняя связана с точкой А через паразитную емкость С_пар. Величина U_н может быть определена по формуле:

, (8.2)

где

 

Рис.8.5.Ёмкостная паразитная связь.

 

Из формулы (8.2) следует, что наведенное напряжение в точке В будет тем больше, чем меньше х_пар и чем больше сопротивление z_в. Комбинация из этих двух сопротивлений представляет собой обычный делитель напряжения.

Рассмотрим частный случай, когда источник наводок работает на частоте ω₀ и настроенный на ту же частоту (рис. 8.6).

 

Рис.8.6.Ёмкостная паразитная связь с резонансным контуром.

Сопротивление в точке В относительно корпуса равно

,

где С – емкость контура,

d_э – эквивалентное затухание контура.

Подставив эти значения в выражение (8.2), получим:

;

при этом полагаем, что х_пар>>z_вх. Отсюда следует, что на контуре возникает часть напряжения источника наводки, определяемая отношением

Таким образом, паразитная емкостная связь с резонансным контуром тем опаснее, чем меньше затухание контура, чем выше его добротность Q, чем уже полоса пропускания . Очевидно, что это относится к частотам, близким к резонансной ω₀ , на которых и проявляется паразитная связь.