
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способ относительных разниц.Содержание книги Поиск на нашем сайте
Это комбинация цепных подстановок и индексов применяется для измерения влияния факторов на прирост результативного пок-ля в случае, если имеются данные анализа в динамике. При использовании метода выполняются все требования цепных подстановок и эллименирования. Для расчета используются темпы прироста по изучаемым факторам. Алгоритм: у =А*В*С; ∆у(∆А)= У0*Тпр (А)/100%; ∆у(∆В)=(У0+∆У(∆А))*Тпр (В)/100%∆; у(∆С)=(У0+∆У(∆А)+∆У(∆В))*Тпр (С)/100%. Достоинства:1)простота и скорость расчетов. Недостатки:1)Невозможность применения в кратных моделях. 2)Зависимость от последовательности подстановки.
18.Индексный метод.
Основывается на относительных пок-лях, выражающих отношение уровня данного явления к уровню его в прошлое время или уровню аналогичного явления, принятому в качестве базы. Индекс исчисляется сопоставлением соизмеряемой (отчетной)величины с базисной. Индивидуальный индекс -выражает соотношение непосредственно соизмеряемых величин; аиндексы, хар-щие соотношение сложных явл-ний называются групповыми, или тотальными. Статистика называет несколько форм индексов. к-ые используются в аналитической работе (агрегатная, арифметическая, гармоническая и др.).Применяя агрегатную форму индекса и соблюдая установленную вычислительную процедуру,можно решить классическую аналитическую задачу:определение влияния на объем произведенной продукции фактора кол-ва и фактора цен. Схема расчета: ∑q1p1-∑q0p0=(∑q1p0-∑q0p0)+ (∑q1p1-∑q1p0), где (∑q1p0-∑q0p0)-влияние кол-ва, (∑q1p1-∑q1p0)-влияние цен. Агрегатный индекс –основная форма всякого индекса, его можно преобразовать в ср.арифметический и в ср.гармонический индексы.Динамика оборота по реализации промышленной продукции должна хар-ться временными рядами, построенными за ряд истекших лет с учетом изменения цен. Индекс объема реализации 9товарооборота),взятый в ценах соответствующих лет,имеет вид: Iqp= I(a) = (a1*b0*c0*d0) / (a0*b0*c0*d0) – факторный индекс, показывающий, как изменяется показатель a. I(b) = (a1*b1*c0*d0) / (a1*b0*c0*d0) – факторный индекс, показывающий, как изменяется показатель b и т.д. I(y) = (a1*b1*c1*d1) / (a0*b0*c0*d0) – так называемый «общий индекс изменений в результирующем показателе» в зависимости от всех факторов. Важно отметить, что при этом: I(y) = I(a)* I(b)* I(c)* I(d). Индексный метод факторного анализа позволяет проводить разложение на факторы и относительных, и абсолютных отклонений в обобщающем показателе. Иными словами, влияние отдельного фактора можно определить при помощи разности числителя и знаменателя соответствующих индексов. Такой принцип разложения по факторам можно использовать в случае, если количество факторов равно двум (количественный и качественный), причем анализируемый показатель представляется в качестве их произведения. Теория индексов не может дать некого обобщенного метода разложения по факторам отклонений определенного обобщающего показателя в случае, если число факторов более 2. Для решения задач такого типа обычно используют метод цепной подстановки.
Интегральный способ. Метод позволяет избежать недостатков метода цепных подстановок, т.е. достигнуть полного разложения отклонения результативного пок-ля по факторам. Метод универсален, т.к. используется в мультипликативных, кратных и смешенных моделях. Недостатком метода явл-ся необходимость использования ср-в техники в моделях более 5-ти факторов. Алгоритм на основе 2ух факторной мультипликативной модели: у =А*В; ∆у(А) = ∆А*Во+(0,5∆А∆В); ∆у(В)= ∆В*Ао+(0,5∆А∆В).
3-ех факторная: у= А*В*С; у∆(∆А) =0,5∆А(В0*С1+В1*С0)+(1/3 *∆А*∆В*∆С); у∆(∆В)=0,5∆В(А0*С1+А1*С0)+(1/3 *∆А*∆В*∆С); у∆(∆С) =0,5∆С(А0*В1+А1*В0)+(1/3 *∆А*∆В*∆С).
4ех факторная: у =АВСД; ∆у(∆А) =1/6 ∆А[3В0С0Д0+В1Д0(С1+∆С)+ Д1С0(В1+∆В)+ С1В0(Д1+∆Д)]+1/4∆А∆В∆С∆Д; ∆у(∆В) =1/6 ∆В[3А0С0Д0+А1Д0(С1+∆С)+ Д1С0(А1+∆А)+ С1А0(Д1+∆Д)]+1/4∆А∆В∆С∆Д; ∆у(∆С) =1/6 ∆А[3А0В0Д0+С1А0(В1+∆В)+ В1Д0(А1+∆А)+ А1В0(Д1+∆Д)]+1/4∆А∆В∆С∆Д; ∆у(∆Д) =1/6 ∆Д[3А0В0С0+В1Д0(С1+∆С)+ В1С0(А1+∆А)+ А1В0(С1+∆С)]+1/4∆А∆В∆С∆Д.
5ти факторная: F =XYZGN;
∆F(x) =1/10*∆X(4Y0Z0G0N0+Y1Z0G0(N1+∆N)+ Z1Y0N0(G1+∆G)+ G1N0Y0(Z1+∆Z)+ N1Z0G0(Y1+∆Y))+1/5∆X∆Y∆G∆Z∆N; ∆F(Y) =1/10*∆Y(4X0Z0G0N0+X1Z0G0(N1+∆N)+ Z1X0N0(G1+∆G)+ G1N0X0(Z1+∆Z)+ N1Z0G0(X1+∆X))+1/5∆X∆Y∆G∆Z∆N; ∆F(Z) =1/10*∆Z(4X0Y0G0N0+Y1X0G0(N1+∆N)+ X1Y0N0(G1+∆G)+ G1N0Y0(X1+∆X)+ N1X0G0(Y1+∆Y))+1/5∆X∆Y∆G∆Z∆N; ∆F(G) =1/10*∆G(4X0Z0Y0N0+Y1Z0X0(N1+∆N)+ Z1Y0N0(X1+∆X)+ X1N0Y0(Z1+∆Z)+ N1Z0X0(Y1+∆Y))+1/5∆X∆Y∆G∆Z∆N; ∆F(N) =1/10*∆N(4Y0Z0G0X0+Y1Z0G0(X1+∆X)+ Z1Y0X0(G1+∆G)+ G1X0Y0(Z1+∆Z)+ X1Z0G0(Y1+∆Y))+1/5∆X∆Y∆G∆Z∆N;
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.89.181 (0.009 с.) |

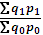 ; Этот индекс отражает изменение кол-ва и цен. Обязательное условие при построение рядов динамики – выражение оборота в одинаковых ценах(базисного периода), т.е. расчет индекса физического объема товарооборота по формуле: Ip=
; Этот индекс отражает изменение кол-ва и цен. Обязательное условие при построение рядов динамики – выражение оборота в одинаковых ценах(базисного периода), т.е. расчет индекса физического объема товарооборота по формуле: Ip=  ; Такой пересчет товарооборота в сопоставимые цены по схеме агрегатного индекса м.б. проведен, если товары учитываются не только посумме, но и по кол-ву.если кол-ный учет не ведется,то физического объема определяется отношением индекса цен, исчисленного по схеме среднего гармонического индекса:: Ip=
; Такой пересчет товарооборота в сопоставимые цены по схеме агрегатного индекса м.б. проведен, если товары учитываются не только посумме, но и по кол-ву.если кол-ный учет не ведется,то физического объема определяется отношением индекса цен, исчисленного по схеме среднего гармонического индекса:: Ip= 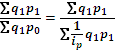 ; где ip=p1/pe. Использовав индексные пересчеты и построив временной ряд можно квалифицированно проанализировать явление динамики. Индексный метод факторного анализа определяется следующим принципом так называемого «построения индексов»: изменением лишь одного фактора, когда остальные остаются неизменны. Предположим, что Y = а* b*с* d. В этом случае:
; где ip=p1/pe. Использовав индексные пересчеты и построив временной ряд можно квалифицированно проанализировать явление динамики. Индексный метод факторного анализа определяется следующим принципом так называемого «построения индексов»: изменением лишь одного фактора, когда остальные остаются неизменны. Предположим, что Y = а* b*с* d. В этом случае:


