Призменная прочность бетона, прочность при растяжении, срезе и скалывании. Прочность при многократном загружении.
Содержание книги
- Классы бетона, изменение прочности во времени.
- Призменная прочность бетона, прочность при растяжении, срезе и скалывании. Прочность при многократном загружении.
- Деформации при многократном повторном загружении. Предельные деформации при сжатии и растяжении.
- Арматурные изделия. Соединения арматуры.
- Основные положения метода расчёта жбк по предельным состояниям. Понятие о предельном состоянии. Сущность расчёта по двум группам предельных состояний.
- Изгибаемые элементы. Сведения о конструкции сборных плит и панелей, балок и других изгибаемых элементов. Армирование изгибаемых элементов
- Сжатые и растянутые элементы. Расчет прочности. Конструктивные особенности сжатых и растянутых элементов.
- Расчет железобетонных конструкций по 2-ой группе предельных состояний. Основные положения расчета.
- Виды каменных и армокаменных конструкций, область их применения. Каменные и армокаменные конструкции жилых, гражданских и промышленных зданий. Расчет элементов каменных конструкций.
- Основные факторы, влияющие на прочность кладки при сжатии. Прочность кирпичной кладки при растяжении, изгибе и срезе. Прочность кладки при местном сжатии.
- Конструкции и расчет стыковых соединений элементов.
- Конструкции одноэтажных каркасных зданий. Нагрузки, действующие на здание. Пространственная работа каркаса при крановых нагрузках. Статический расчет рамы.
- Клонны сплошные прямоугольного сечения и сквозные двухветвевые. Особенности расчета и конструирования колонн.
- Конструкции покрытий. Железобетонные панели покрытий (ребристые, двойное т, кжс, и др. ), их конструктивные решения. Классификация ферм покрытий.
- Конструкции сборных и монолитных фундаментов. Расчет центрально и внецентренно нагруженных фундаментов стаканного типа под колонны.
Похожие статьи вашей тематики
Прочность – способность тела сопротивляться внешним воздействиям, не разрушаясь. Существуют различные виды прочности бетона.
  Кубиковая прочность. Определяется при испытании на сжатие под прессом кубов бетона, изготовленных в тех же условиях, что и конструкция. Эталонный образец – куб размером 150х150х150 мм, хранившийся при t = 20±2°С и влажности 90-100% в течение 28 сут. и испытанный в нормальных условиях (t = 20±2°С и влажность 65%). Предел прочности куба при разрушении – кубиковая прочность. Применяют кубы с другими размерами ребра (100 или 200 мм), в этом случае в расчёты вводится масштабный коэффициент: Кубиковая прочность. Определяется при испытании на сжатие под прессом кубов бетона, изготовленных в тех же условиях, что и конструкция. Эталонный образец – куб размером 150х150х150 мм, хранившийся при t = 20±2°С и влажности 90-100% в течение 28 сут. и испытанный в нормальных условиях (t = 20±2°С и влажность 65%). Предел прочности куба при разрушении – кубиковая прочность. Применяют кубы с другими размерами ребра (100 или 200 мм), в этом случае в расчёты вводится масштабный коэффициент: 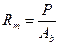
Призменная прочность. Предел прочности призмы при разрушении принимают за призменную прочность. Определяется при испытании на сжатие призм размером 150х150х600 мм (или 100х100х400 мм), т.к. при отношении высоты призмы к ребру основания ≥4 трение на работу призмы не влияет. Призменная прочность больше соответствует прочности бетона на сжатие в реальных конструкциях ещё и потому, что форма призмы больше напоминает конфигурацию изделий или конструкций. При испытании призмы прочность определяют делением разрушающей силы на площадь. Зависимость призменной прочности от кубиковой установлена экспериментально:  ; ;
  - для тяжёлого бетона; - для тяжёлого бетона;  - для лёгких (ячеистых) бетонов - для лёгких (ячеистых) бетонов
Прочность при осевом растяжении. Ориентировочно можно определить по формуле Фере: 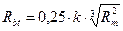
k = 0,8 – для бетона класса ≤ В25; k = 0,7 – для бетона класса ≥ В30
Призм. прочность при растяжении в 10 – 20 раз < прочности бетона при сжатии.
Прочность при срезе. ЖБК редко работают на срез, который обычно сопровождается действием продольных сил. Сопротивление срезу может возникать в шпоночных соединениях и у опор балок.

 Прочность при скалывании. Сопровождается действием поперечных сил и может определяться по формуле: Прочность при скалывании. Сопровождается действием поперечных сил и может определяться по формуле:
 , ,
γ – масштабный коэффициент.
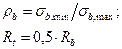 Прочность при многократном загружении. Под прочностью бетона при многократно повторных (подвижных или пульсирующих) нагрузках понимают напряжение, при котором количество циклов, необходимых для разрушения образца, составляет не менее 106. Эта прочность – выносливость. Прочность бетона в этом случае зависит от количества циклов, кот. характеризуется ассиметрией цикла: Прочность при многократном загружении. Под прочностью бетона при многократно повторных (подвижных или пульсирующих) нагрузках понимают напряжение, при котором количество циклов, необходимых для разрушения образца, составляет не менее 106. Эта прочность – выносливость. Прочность бетона в этом случае зависит от количества циклов, кот. характеризуется ассиметрией цикла:
4 Деформации бетона при кратковременном и длительном загружении. Ползучесть бетона и релаксация напряжений. Усадка бетона.
При загружении бетона кратковременной нагрузкой развиваются упругие и неупругие деформации.
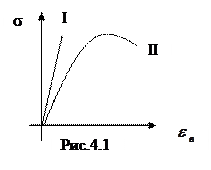  Упругие деформации, как правило, наблюдаются на первоначальном этапе загружения, и их величина зависит от скорости загружения. При мгновенной скорости загружения можно наблюдать только упругие деформации. Если образец загружать по этапам и замерять деформации на каждой ступени дважды (сразу после приложения нагрузки и через время после выдержки под нагрузкой) получится ступенчатая линия, которую можно объединить в диаграмму (рис. 4.1) Упругие деформации, как правило, наблюдаются на первоначальном этапе загружения, и их величина зависит от скорости загружения. При мгновенной скорости загружения можно наблюдать только упругие деформации. Если образец загружать по этапам и замерять деформации на каждой ступени дважды (сразу после приложения нагрузки и через время после выдержки под нагрузкой) получится ступенчатая линия, которую можно объединить в диаграмму (рис. 4.1)
I - при мгновенном загружении II - полные деформации при ступенчатом загружении При достаточно большом числе ступеней загружения зависимость между напряжениями и деформациями может быть изображена плавной кривой (рис.4.2).
  Из диаграммы 4.2 видно, что при небольших нагружениях s в <0,2R в (участок О-1) бетон можно рассматривать как упругий материал; 0,2R в <s в <0,5R в (участок 1-2) возникают неупругие деформации, вызванные уплотнение геля и после образования микро трещин (точка 2) рост деформации становится более интенсивнее (участок 2-3) при дальнейшем увеличении нагрузки микротрещины объединяются и образец начинает разрушаться (точка 4) напряжения в этой точке равны R в , а деформации бетона равны (предельным); участок 4-5 нисходящей диаграммы характеризует падение сопротивления бетона и падение нагрузки. При длительном действии нагрузки пластические деформации бетона продолжают развиваться, как показывают опыты в течение 3-4 лет и более с меньшей интенсивностью. Наибольшие деформации появляются в 3-4месяца действия нагрузки. Из диаграммы 4.2 видно, что при небольших нагружениях s в <0,2R в (участок О-1) бетон можно рассматривать как упругий материал; 0,2R в <s в <0,5R в (участок 1-2) возникают неупругие деформации, вызванные уплотнение геля и после образования микро трещин (точка 2) рост деформации становится более интенсивнее (участок 2-3) при дальнейшем увеличении нагрузки микротрещины объединяются и образец начинает разрушаться (точка 4) напряжения в этой точке равны R в , а деформации бетона равны (предельным); участок 4-5 нисходящей диаграммы характеризует падение сопротивления бетона и падение нагрузки. При длительном действии нагрузки пластические деформации бетона продолжают развиваться, как показывают опыты в течение 3-4 лет и более с меньшей интенсивностью. Наибольшие деформации появляются в 3-4месяца действия нагрузки.
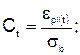   Участок О-1 - упругие деформации - при загружении кривизна диаграммы зависит от скорости загружения образца; участок 1-2 характеризует рост пластических деформаций за время выдержки при постоянном загружении. Прирост пластических деформаций постепенно затухает, а их величина стремится к предельному значению. Свойство бетона, характеризующееся нарастанием пластических деформаций при длительном действии нагрузки, называется ползучестью бетона. Эти деформации (силовые) могут в 3-4 раза превышать упругие деформации при длительном действии постоянной нагрузки. Если деформации ползучести нарастают свободно, то напряжения в бетоне остаются величиной постоянной. Когда ползучесть ограниченна или стеснена, то напряжения в бетоне уменьшаются. Свойство бетона, характеризующееся уменьшением с течением времени напряжений при постоянной начальной деформативности называется релаксацией напряжений. Ползучесть и релаксация имеют общую природу, обусловленную структурой бетона и, оказывают влияние на работу ЖБК. Опыты показали, что, независимо с какой скорость было достигнуто напряжения, конечные деформации ползучести будут с течением времени одинаковыми. Различают линейную и нелинейную ползучесть. Линейная ползучесть имеет место при s в <0,5R в, которая обусловлена главным образом уплотнением геля, при этом происходит перераспределение напряжений под нагрузкой с гелевой структуры на цементный камень и заполнитель. При s в >0,5R в возникают микротрещины и нарушается линейная зависимость и наступает нелинейная ползучесть. Для количественного определения деформации ползучести при сжатии вводят понятия меры ползучести Ct - представляет собой относительную деформацию ползучести в момент времени t соответствующей приращению ползучести и характеристики ползучести wt - отношение деформации ползучести в момент времени t к мгновенной деформации. Участок О-1 - упругие деформации - при загружении кривизна диаграммы зависит от скорости загружения образца; участок 1-2 характеризует рост пластических деформаций за время выдержки при постоянном загружении. Прирост пластических деформаций постепенно затухает, а их величина стремится к предельному значению. Свойство бетона, характеризующееся нарастанием пластических деформаций при длительном действии нагрузки, называется ползучестью бетона. Эти деформации (силовые) могут в 3-4 раза превышать упругие деформации при длительном действии постоянной нагрузки. Если деформации ползучести нарастают свободно, то напряжения в бетоне остаются величиной постоянной. Когда ползучесть ограниченна или стеснена, то напряжения в бетоне уменьшаются. Свойство бетона, характеризующееся уменьшением с течением времени напряжений при постоянной начальной деформативности называется релаксацией напряжений. Ползучесть и релаксация имеют общую природу, обусловленную структурой бетона и, оказывают влияние на работу ЖБК. Опыты показали, что, независимо с какой скорость было достигнуто напряжения, конечные деформации ползучести будут с течением времени одинаковыми. Различают линейную и нелинейную ползучесть. Линейная ползучесть имеет место при s в <0,5R в, которая обусловлена главным образом уплотнением геля, при этом происходит перераспределение напряжений под нагрузкой с гелевой структуры на цементный камень и заполнитель. При s в >0,5R в возникают микротрещины и нарушается линейная зависимость и наступает нелинейная ползучесть. Для количественного определения деформации ползучести при сжатии вводят понятия меры ползучести Ct - представляет собой относительную деформацию ползучести в момент времени t соответствующей приращению ползучести и характеристики ползучести wt - отношение деформации ползучести в момент времени t к мгновенной деформации.
|




 Кубиковая прочность. Определяется при испытании на сжатие под прессом кубов бетона, изготовленных в тех же условиях, что и конструкция. Эталонный образец – куб размером 150х150х150 мм, хранившийся при t = 20±2°С и влажности 90-100% в течение 28 сут. и испытанный в нормальных условиях (t = 20±2°С и влажность 65%). Предел прочности куба при разрушении – кубиковая прочность. Применяют кубы с другими размерами ребра (100 или 200 мм), в этом случае в расчёты вводится масштабный коэффициент:
Кубиковая прочность. Определяется при испытании на сжатие под прессом кубов бетона, изготовленных в тех же условиях, что и конструкция. Эталонный образец – куб размером 150х150х150 мм, хранившийся при t = 20±2°С и влажности 90-100% в течение 28 сут. и испытанный в нормальных условиях (t = 20±2°С и влажность 65%). Предел прочности куба при разрушении – кубиковая прочность. Применяют кубы с другими размерами ребра (100 или 200 мм), в этом случае в расчёты вводится масштабный коэффициент: 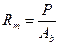
 ;
;
 - для тяжёлого бетона;
- для тяжёлого бетона;  - для лёгких (ячеистых) бетонов
- для лёгких (ячеистых) бетонов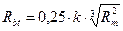

 Прочность при скалывании. Сопровождается действием поперечных сил и может определяться по формуле:
Прочность при скалывании. Сопровождается действием поперечных сил и может определяться по формуле: ,
,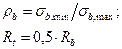 Прочность при многократном загружении. Под прочностью бетона при многократно повторных (подвижных или пульсирующих) нагрузках понимают напряжение, при котором количество циклов, необходимых для разрушения образца, составляет не менее 106. Эта прочность – выносливость. Прочность бетона в этом случае зависит от количества циклов, кот. характеризуется ассиметрией цикла:
Прочность при многократном загружении. Под прочностью бетона при многократно повторных (подвижных или пульсирующих) нагрузках понимают напряжение, при котором количество циклов, необходимых для разрушения образца, составляет не менее 106. Эта прочность – выносливость. Прочность бетона в этом случае зависит от количества циклов, кот. характеризуется ассиметрией цикла:
 Упругие деформации, как правило, наблюдаются на первоначальном этапе загружения, и их величина зависит от скорости загружения. При мгновенной скорости загружения можно наблюдать только упругие деформации. Если образец загружать по этапам и замерять деформации на каждой ступени дважды (сразу после приложения нагрузки и через время после выдержки под нагрузкой) получится ступенчатая линия, которую можно объединить в диаграмму (рис. 4.1)
Упругие деформации, как правило, наблюдаются на первоначальном этапе загружения, и их величина зависит от скорости загружения. При мгновенной скорости загружения можно наблюдать только упругие деформации. Если образец загружать по этапам и замерять деформации на каждой ступени дважды (сразу после приложения нагрузки и через время после выдержки под нагрузкой) получится ступенчатая линия, которую можно объединить в диаграмму (рис. 4.1)
 Из диаграммы 4.2 видно, что при небольших нагружениях s в <0,2R в (участок О-1) бетон можно рассматривать как упругий материал; 0,2R в <s в <0,5R в (участок 1-2) возникают неупругие деформации, вызванные уплотнение геля и после образования микро трещин (точка 2) рост деформации становится более интенсивнее (участок 2-3) при дальнейшем увеличении нагрузки микротрещины объединяются и образец начинает разрушаться (точка 4) напряжения в этой точке равны R в , а деформации бетона равны (предельным); участок 4-5 нисходящей диаграммы характеризует падение сопротивления бетона и падение нагрузки. При длительном действии нагрузки пластические деформации бетона продолжают развиваться, как показывают опыты в течение 3-4 лет и более с меньшей интенсивностью. Наибольшие деформации появляются в 3-4месяца действия нагрузки.
Из диаграммы 4.2 видно, что при небольших нагружениях s в <0,2R в (участок О-1) бетон можно рассматривать как упругий материал; 0,2R в <s в <0,5R в (участок 1-2) возникают неупругие деформации, вызванные уплотнение геля и после образования микро трещин (точка 2) рост деформации становится более интенсивнее (участок 2-3) при дальнейшем увеличении нагрузки микротрещины объединяются и образец начинает разрушаться (точка 4) напряжения в этой точке равны R в , а деформации бетона равны (предельным); участок 4-5 нисходящей диаграммы характеризует падение сопротивления бетона и падение нагрузки. При длительном действии нагрузки пластические деформации бетона продолжают развиваться, как показывают опыты в течение 3-4 лет и более с меньшей интенсивностью. Наибольшие деформации появляются в 3-4месяца действия нагрузки.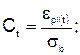

 Участок О-1 - упругие деформации - при загружении кривизна диаграммы зависит от скорости загружения образца; участок 1-2 характеризует рост пластических деформаций за время выдержки при постоянном загружении. Прирост пластических деформаций постепенно затухает, а их величина стремится к предельному значению. Свойство бетона, характеризующееся нарастанием пластических деформаций при длительном действии нагрузки, называется ползучестью бетона. Эти деформации (силовые) могут в 3-4 раза превышать упругие деформации при длительном действии постоянной нагрузки. Если деформации ползучести нарастают свободно, то напряжения в бетоне остаются величиной постоянной. Когда ползучесть ограниченна или стеснена, то напряжения в бетоне уменьшаются. Свойство бетона, характеризующееся уменьшением с течением времени напряжений при постоянной начальной деформативности называется релаксацией напряжений. Ползучесть и релаксация имеют общую природу, обусловленную структурой бетона и, оказывают влияние на работу ЖБК. Опыты показали, что, независимо с какой скорость было достигнуто напряжения, конечные деформации ползучести будут с течением времени одинаковыми. Различают линейную и нелинейную ползучесть. Линейная ползучесть имеет место при s в <0,5R в, которая обусловлена главным образом уплотнением геля, при этом происходит перераспределение напряжений под нагрузкой с гелевой структуры на цементный камень и заполнитель. При s в >0,5R в возникают микротрещины и нарушается линейная зависимость и наступает нелинейная ползучесть. Для количественного определения деформации ползучести при сжатии вводят понятия меры ползучести Ct - представляет собой относительную деформацию ползучести в момент времени t соответствующей приращению ползучести и характеристики ползучести wt - отношение деформации ползучести в момент времени t к мгновенной деформации.
Участок О-1 - упругие деформации - при загружении кривизна диаграммы зависит от скорости загружения образца; участок 1-2 характеризует рост пластических деформаций за время выдержки при постоянном загружении. Прирост пластических деформаций постепенно затухает, а их величина стремится к предельному значению. Свойство бетона, характеризующееся нарастанием пластических деформаций при длительном действии нагрузки, называется ползучестью бетона. Эти деформации (силовые) могут в 3-4 раза превышать упругие деформации при длительном действии постоянной нагрузки. Если деформации ползучести нарастают свободно, то напряжения в бетоне остаются величиной постоянной. Когда ползучесть ограниченна или стеснена, то напряжения в бетоне уменьшаются. Свойство бетона, характеризующееся уменьшением с течением времени напряжений при постоянной начальной деформативности называется релаксацией напряжений. Ползучесть и релаксация имеют общую природу, обусловленную структурой бетона и, оказывают влияние на работу ЖБК. Опыты показали, что, независимо с какой скорость было достигнуто напряжения, конечные деформации ползучести будут с течением времени одинаковыми. Различают линейную и нелинейную ползучесть. Линейная ползучесть имеет место при s в <0,5R в, которая обусловлена главным образом уплотнением геля, при этом происходит перераспределение напряжений под нагрузкой с гелевой структуры на цементный камень и заполнитель. При s в >0,5R в возникают микротрещины и нарушается линейная зависимость и наступает нелинейная ползучесть. Для количественного определения деформации ползучести при сжатии вводят понятия меры ползучести Ct - представляет собой относительную деформацию ползучести в момент времени t соответствующей приращению ползучести и характеристики ползучести wt - отношение деформации ползучести в момент времени t к мгновенной деформации.


