
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случай равномерного распределения узлов интерполяцииСодержание книги
Поиск на нашем сайте
В случае равномерного распределения узлов интерполяции xi выражаются через расстояние между узлами интерполяции h и начальную точку x 0:
и, следовательно,
Подставив эти выражения в формулу базисного полинома и вынеся h за знаки перемножения в числителе и знаменателе, получим
Теперь можно ввести замену переменной
и получить полином от y, который строится с использованием только целочисленной арифметики. Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования длинной арифметики. Сплайн Эрмита (cubic Hermite) — сплайн, построенный из многочленов в форме Эрмита. Некоторая функция f(x) задана на отрезке [ a, b ], разбитом на части [ xi − 1, xi ], a = x 0 < x 1 <... < xN = b. Кубическим сплайном дефекта 1 называется функция S (x), которая:
Рациональная интерполяция (интерполяция рациональными функциями) — представление интерполируемой функции f (x) (точнее говоря, ряда табличных значений) в виде отношения двух полиномов. Ряд функций, плохо интерполируемых полиномиальными методами, удаётся хорошо приблизить рациональной функцией с полиномом в числителе и знаменателе. Особенно это касается функций с нерегулярным характером поведения (в частности, рациональная интерполяция хорошо подходит для функций с особыми точками и резкими изменениями). По известным n точкам f (x 1), …, f (xn) приближение к f (x) ищется в виде
Коэффициенты ai и bi вычисляются из набора соотношений R (xj) = f (xj), где
Эти уравнения образуют систему линейных алгебраических уравнений из n уравнений относительно n + 1 неизвестных. Классическая задача интерполяции сводится к решению этой системы, однако качественное и численное исследование такой системы затруднительно. К тому же при большом количестве точек вычислить коэффициенты с большой точностью сложно — небольшой погрешности достаточно для того, чтобы полученный рациональный интерполянт не проходил через заданные точки.
Билинейная интерполяция — расширение линейной интерполяции для функций двух переменных. Ключевая идея заключается в том, чтобы провести обычную линейную интерполяцию сначала в одном направлении, затем в другом. Результат билинейной интерполяции не зависит от порядка шагов. Возможно сначала интерполировать между известными точками вдоль оси ординат и затем, получив два вспомогательных значения, интерполировать между ними вдоль оси абсцисс. Результат будет тот же. Очевидное расширение билинейной интерполяции на функции трех переменных - трилинейная интерполяция. Бикубическая интерполяция — в вычислительной математике расширение кубической интерполяции на случай функции двух переменных, значения которой заданы на двумерной регулярной сетке. Поверхность, полученная в результате бикубической интерполяции является гладкой функцией, в отличие от поверхностей, полученных в результате билинейной интерполяции или интерполяции методом ближайшего соседа. Так же бикубическая интерполяция часто используется в обработке изображений, давая более качественное изображение по сравнению с билинейной интерполяцией. В случае бикубической интерполяции значение функции в искомой точке вычисляется через ее значения в 16-ти соседних точках.
РАБОЧЕЕ ЗАДАНИЕ
7. Запустить ВП 1D Interpolation.vi 8. Пронаблюдать влияние метода интерполяции на конечный результат. Объяснить полученные результаты. 9. Изменить набор данных и пронаблюдать влияние метода интерполяции как в пункте 2. Объяснить полученные результаты. 10. Запустить ВП Interpolation Solver.vi 11. Пронаблюдать влияние метода интерполяции на конечный результат. Объяснить полученные результаты. 12. Изменяя значение входных точек и точек интерполяции пронаблюдать влияние метода интерполяции на конечный результат. Объяснить полученные результаты. 13. Запустить ВП 2D Interpolation.vi 14. Пронаблюдать влияние метода интерполяции на конечный результат. Объяснить полученные результаты. Контрольные вопросы: 1. Почему при изображении спектра мощности на график выводится частоты только ниже частоты Найквиста? 2. Почему при некратных значениях N и частоты отсчетов спектр испытывает колебания?
3. Почему количество периодов синусоиды зависит от N? (кол-во точек FTT) 4. Какую роль играет частота оцифровки? 5. Чему равна частота Найквиста? 6. Чем отличаются цифровой и аналоговый сигналы? 7. Почему спектр реального и оцифрованного сигналов не всегда совпадают? 8. Что такое алиасинг? 9. Как вы объясните причины возникновения алиасинга? 10. Объясните на примерах, как используя теоремы Котельникова надо выбирать частоту оцифровки? 11. Можно ли, ничего не зная о спектре входного сигнала и работая только с оцифрованным выяснить, правильно ли выбрана частота оцифровки? Если можно то как? 12. Как влияет длительность окна на ширину спектра тонального спектра сигнала? 13. Как влияет тип временного окна на тип спектра сигнала? 14. Какой вид временного окна вы выберете, если вам необходимо выделить два сигнала с близкими частотами? 15. Какая роль спектральной характеристики окна. 16. Почему всегда используются временные окна? 17. Какова должна быть длительность временного окна, чтобы различить сигнал с амплитудой в 10 раз меньше, чем уровень шума, если полоса частот сигнала (шум) – 1 кГц?
Требования к оформлению отчёта Отчёт должен содержать: - титульный лист с наименованием учебного заведения, кафедры, курса, лабораторной работы, фамилией и подписью студента; - указание цели работы; - написать задачи; - описание объектов исследования; - результаты выполнения работы; - ответы на контрольные вопросы; - заключение, в котором приводится краткое перечисление выполненных действий, полученных результатов и сделанные из этих результатов выводы.
|
||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.17.137 (0.009 с.) |

 ,
,

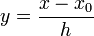
 , и p + q + 1 = n.
, и p + q + 1 = n. , которые можно записать в виде
, которые можно записать в виде , где
, где 



