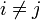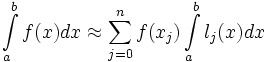Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типовые сигналы и их спектрыСтр 1 из 5Следующая ⇒
Лабораторная работа №1 Типовые сигналы и их спектры Цель лабораторной работы: В рамках данной лабораторной работы необходимо исследовать спектральные характеристики некоторых типовых сигналов, показать зависимость изменения спектральных характеристик этих сигналов от изменения их характеристик во временной области, а также рассмотреть различные виды модуляции сигналов.
Теоретическая часть Пусть дана функция s(t), описывающая исследуемый сигнал (процесс). Для данной функции существует прямое преобразование Фурье вида
если выполняются следующие условия:
Обратное преобразование Фурье задается следующим образом
Преобразование Фурье ставит в соответствие сигналу s(t), заданному во времени, его спектральную функцию (спектр) Спектр периодического сигнала является дискретным и представляет набор гармонических колебаний, в сумме составляющий исходный сигнал. Модуль спектральной функции
При создании систем передачи информации в большинстве случаев оказывается, что спектр исходного сигнала, подлежащего передаче, сосредоточен отнюдь не на тех частотах, которые эффективно пропускает имеющийся канал связи. Кроме того, очень часто необходимо в одном и том же канале связи передавать несколько сигналов одновременно. Одним из способов решения этой задачи является использование частотного разделения каналов, при котором разные сигналы занимают неперекрывающиеся полосы частот. Решение указанной проблемы достигается при использовании модуляции, сущность которой заключается в следующем. Формируется некоторое колебание (чаще всего гармоническое), называемое несущим колебанием или просто несущей и какой-либо из параметров этого колебания изменяется во времени пропорционально исходному сигналу. Исходный сигнал называют модулирующим, а результирующее колебание с изменяющимися во времени параметрами — модулированным сигналом. Обратный процесс — выделение модулирующего сигнала из модулированного колебания — называется демодуляцией.
Существуют различные виды модуляции:
Амплитудная модуляция сигнала - модуляция сигнала, изменяющая амплитуды несущей. При амплитудной модуляции высокий потенциал соответствует "единице", низкий - "нулю". Амплитудная модуляция соответствует переносу информации s(t) Þ U(t) при постоянных значениях параметров несущей частоты w и j.
Частотная модуляция сигнала - модуляция сигнала, в которой сигналы 0 и 1 передаются синусоидами, имеющими различные частоты. Частотная модуляция характеризуется линейной связью модулирующего сигнала с мгновенной частотой колебаний, при которой мгновенная частота колебаний образуется сложением частоты высокочастотного несущего колебания wo со значением амплитуды модулирующего сигнала с определенным коэффициентом пропорциональности:
w(t) = wo + k×s(t).
Фазовая модуляция - модуляция, в которой при изменении от "нуля" к "единице" и от "единицы" к "нулю" фаза синусоидальной несущей изменяется на 180 градусов. При фазовой модуляции значение фазового угла постоянной несущей частоты колебаний wo пропорционально амплитуде модулирующего сигнала s(t). Уравнение Фазовой модуляции сигнала определяется выражением
u(t) = Um cos[wot + k×s(t)], где k – коэффициент пропорциональности.
Рабочее задание
1. Запустить ВП Spectrum measurements.vi 2. Изменяя частоту входного сигнала пронаблюдать изменения спектра сигнала (логарифмическая и линейная шкалы) 3. Объяснить поведение спектра при значениях частот не кратных 10 4. Запустить ВП Amplitude spectrum (sim).vi
5. Отключить оконный фильтр (в окне window выбрать none) 6. Пронаблюдать амплитудные спектры для всех типов сигналов (синус, треугольник, пила, прямоугольный сигнал) на разных частотах. Объяснить полученные результаты
Рис. 1.1 Рабочий интерфейс ВП Spectrum measurements.vi
Рис. 1.2 Блок-диаграмма ВП Spectrum measurements.vi
Рис. 1.3 Рабочий интерфейс ВП Amplitude spectrum (sim).vi
Рис. 1.4 Блок-диаграмма ВП Amplitude spectrum (sim).vi
Лабораторная работа №2. Теоретическая часть. Большинство реальных сигналов (например, звуковых) являются непрерывными функциями. Для обработки на компьютере требуется перевести сигналы в цифровую форму. Один из способов это сделать – равномерно по времени измерить значения сигнала на определенном промежутке времени и ввести полученные значения амплитуд в компьютер. Если делать измерения достаточно часто, то по полученному дискретному сигналу можно будет достаточно точно восстановить вид исходного непрерывного сигнала. Процесс замера величины сигнала через равные промежутки времени называется равномерной (по времени) дискретизацией. Многие устройства ввода данных в компьютер осуществляют дискретизацию. Например, звуковая карта дискретизирует сигнал с микрофона, сканер дискретизирует сигнал, поступающий с фотоэлемента. В результате дискретизации непрерывный (аналоговый) сигнал прееводится в последовательность чисел. Устройство, выполняющее этот процесс, называется аналогово- цифровым преобразователем (АЦП, analog-to-digital converter, ADC). Частота, с которой АЦП производит замеры аналогового сигнала и выдает его цифровые значения, называется частотой дискретизации.
Рис.2.1Преобразование аналогового сигнала в цифровой Встает вопрос, а при каких условиях на исходный сигнал и на частоту дискретизации можно с необходимой степенью точности восстановить исходный сигнал по его цифровым значениям? Ответ на этот вопрос дает важная теорема Котельникова. Однако, чтобы ее понять, необходимо познакомиться с понятием спектра непрерывного сигнала. Как известно из анализа, любая непрерывная функция может быть разложена на конечном отрезке в ряд Фурье. Смысл этого разложения состоит в том, что функция представляется в виде суммы ряда синусоид с различными амплитудами и фазами и с кратными частотами. Коэффициенты (амплитуды) при синусоидах называются спектром функции. У относительно гладких функций спектр быстро убывает (с ростом номера коэффициенты быстро стремятся к нулю). Для относительно «изрезанных» функций спектр убывает медленно, т.к. для представления разрывов и «изломов функции нужны синусоиды с большими частотами. Говорят, что сигнал имеет ограниченный спектр, если после определенного номера все коэффициенты спектра равны нулю. Другими словами, на заданном отрезке сигнал представляется в виде конечной суммы ряда Фурье. В этом случае говорят, что спектр сигнала лежит ниже частоты F (ограничен частотой F), где F – частота синусоиды при последнем ненулевом коэффициенте ряда Фурье. Теорема Котельникова-Найквиста-Шеннона: если сигнал таков, что его спектр ограничен частотой F, то после дискретизации сигнала с частотой не менее 2F можно восстановить исходный непрерывный сигнал по полученному цифровому сигналу абсолютно точно. Для этого нужно проинтерполировать цифровой сигнал «между отсчетами» специального вида функциями.
На практике эта теорема имеет огромное значение. Например, известно, что большинство звуковых сигналов можно с некоторой степенью точности считать ограниченными спектром. Их спектр, в основном, лежит ниже 20 кГц. Это значит, что при дискретизации с частотой не менее 40 кГц, мы можем потом более-менее точно восстановить исходный аналоговый сигнал по его цифровым отсчетам. Абсолютной точности достичь не удастся, так как в природе не бывает сигналов с идеально ограниченным спектром. Устройство, которое интерполирует дискретный сигнал до непрерывного, называется цифро-аналоговым преобразователем (ЦАП, digital-to-analogue converter, DAC). Эти устройства применяются, например, в проигрывателях компакт-дисков для восстановления звука по цифровому звуковому сигналу, записанному на компакт-диск. Частота дискретизации звукового сигнала при записи на компакт-диск составляет 44100 Гц. Таким образом, и ЦАП на CD-плеере работает на частоте 44100 Гц.
Наложение спектров (алиасинг) Что произойдет, если попытаться оцифровать сигнал с недостаточной для него частотой дискретизации (или если спектр сигнала не ограничен)? В этом случае по полученной цифровой выборке нельзя будет верно восстановить исходный сигнал. Восстановленный сигнал будет выглядеть таким образом, как если бы частоты, лежащие выше половины частоты дискретизации, отразились от половины частоты дискретизации, перешли в нижнюю часть спектра и наложились на частоты, уже присутствующие в нижней части спектра. Этот эффект называется наложением спектров или алиасингом (aliasing). Предположим, что мы попытались оцифровать музыку, спектр которой ограничен 20 кГц, но при записи какой-то электроприбор (например дисплей) сгенерировал сильную помеху с ультразвуковой частотой 39 кГц, которая проникла в налоговый звуковой сигнал. Мы производим оцифровку с частотой 44.1 кГц. При этом мы предполагаем, что звук, лежащий ниже частоты
Таким образом, мы видим, что алиасинг – нежелательное явление при дискретизации сигнала. Например, при оцифровке изображения алиасинг может привести к дефектам в изображении, таким как «блочные», «пикселизованные» границы или муар. Чтобы избежать это явление, необходимо во-первых, использовать более высокую частоту дискретизации, чтобы весь спектр записываемого сигнала уместился ниже половины частоты дискретизации. Во-вторых: искусственно ограничить спектр сигнала перед оцифровкой.
Теоретическая часть Разложению в ряд Фурье могут подвергаться периодические сигналы. При этом они представляются в виде суммы гармонических функций, либо комплексных экспонент с частотами, образующими арифметическую прогрессию. Чтобы такое разложение существовало, фрагмент сигнала длительностью в один период должен удовлетворять условиям Дирихле:
· не должно быть разрывов второго рода (с уходящими в бесконечность ветвями функции); · число разрывов первого рода (скачков) должно быть конечным; · число экстремумов должно быть конечным (в качестве примера функции, которая на конечном интервале имеет бесконечное число экстремумов, можно привести sin(1/x) в окрестностях нуля).
Дискретное преобразование Фурье, по возможности вычисляемое быстрыми методами, лежит в основе различных технологий спектрального анализа, предназначенных для исследования случайных процессов. Дело в том, что если анализируемый сигнал представляет собой случайный процесс, то простое вычисление его ДПФ обычно не представляет большого интереса, так как в результате получается лишь спектр единственной реализации процесса. Поэтому для спектрального анализа случайных сигналов необходимо использовать усреднение спектра. Такие методы, в которых используется только информация, извлеченная из самого входного сигнала, называются непараметрическими. Другой класс методов предполагает наличие некоторой статистической модели случайного сигнала. Процесс спектрального анализа в данном случае включает в себя определение параметров этой модели, и потому такие методы называются параметрическими. Пусть последовательность отсчетов {x(k)} является периодической с периодом N:
Такая последовательность полностью описывается конечным набором чисел, в качестве которого можно взять произвольный фрагмент длиной N, например {x(k)}, k=0,1,…,N-1. Поставленный в соответствие этой последовательности сигнал из смещенных по времени дельта-функций:
также, будет с периодическим с минимальным периодом NT. Так как сигнал (2.2) является дискретным, его спектр должен быть периодическим с периодом Итак, периодический дискретный сигнал имеет периодический дискретный спектр, который также описывается конечным набором из N чисел (один период спектра содержит
Одно из преимуществ частотного представления линейных стационарных систем заключается в том, что интерпретация их поведения получается довольно легко. Многие из последовательностей выражаются через интеграл Фурье вида , где Формулы (2.3) и (2.4) называют представлением, или преобразованием Фурье, а саму функцию
Где Фурье-образ – комплекснозначная функция от
Величины Свойства ДПФ N-членная последовательность N-точечное ДПФ
Заметим, что все свойства сформулирвоанны для конечных последовательностей x[n] и X[k], определенных на интервале [0; N-1]. Обе последовательности имеют нулевые отсчеты вне этого отрезка. Стоит отметить, что нулевая гармоника является суммой значений сигнала. Теоретическая часть Быстрое преобразование Фурье Главная идея быстрого вычисления ДПФ - использование метода “разделяй-и-властвуй”. Вектор делится на части, результаты обработки которых затем сливаются. Будем рассматривать только векторы длины Разделим общую сумму на две: первая содержит слагаемые с четными индексами, вторая с нечетными
Получившиеся равенство дает способ вычислять k- коэффициент ДПФ вектора длины N через два преобразования длины N\2, одно из которых применяется к вектору Чтобы полностью выразить N-значное ДПФ в терминах N/2 – значного преобразования, рассмотрим два случая. При
Окно — весовая функция, которая используется для управления эффектами, обусловленными наличием боковых лепестков в спектральных оценках (растеканием спектра). Имеющуюся конечную запись данных или имеющуюся конечную корреляционную последовательность удобно рассматривать как некоторую часть соответствующей бесконечной последовательности, видимую через применяемое окно. Например, последовательность наблюдаемых данных x0[n] из N отсчётов математически можно записать как произведение прямоугольной функции единичной амплитуды
и бесконечной последовательности x[n]
При этом принимается очевидное допущение, что все ненаблюдаемые отсчёты равны нулю независимо от того, так ли это на самом деле или нет. Дискретное преобразование Фурье (ДПФ) взвешенное окном последовательности, выраженной через преобразование последовательности x[n] и прямоугольного окна rect[n], равно свёртке этих преобразований X0(f) = X(f) * DN(f),
где DN(f) является дискретной функцией sinc, или ядром Дирихле, представляющим собой ДПФ прямоугольной функции. [1] [1] http://ru.wikipedia.org/wiki/Окно_(весовая_функция)
рис. 4.1 рабочий интерфейс ВП Windowing.vi
рис. 4.2 Блок-диаграма ВП Windowing.vi
Запускаем ВП ВП Влияние временного окна на спектр разрешение.vi: 0. Если возникнут проблемы при запуске, то запустите файл Windowing.exe из папки Windowing 1.Задаем параметры Tone 0, WinSeting – меняем разные окна и наблюдаем то подавление, которое присутствует. 2.найти то, окно которое обеспечивает максимально подавление ложных частот. Объясните полученные результаты. 3.Найти то, окно которое обеспечивает минимальное подавление ложных частот. Объясните полученные результаты. 4.Убедиться, что окно влияет на результирующий спектр синусоидального сигнала. Объясните это влияние. 5.Рассматриваем влияние длинны временного окна, работаем с автоскалингом. 6.Выяснить влияет ли длинна временного окна на спектр и объясните, если влияет то почему именно таким образом. 7.Что происходит при изменеии длинны временного окна? 8.Убедиться, что на разных окнах происходит одно и тоже самое 9.Ставим 2 частоты, различающихся на 10 Гц. 1 Вольт и 10 Вольт. Изменяя окна и длительность временного окна выясняем, какое окно разделяет лучше всего. 10. Далее повторите 9 пункт для 1 и 50 Вольт и для частот, различающихся на 20 и 30 Гц. Объясните полученные результаты. Повторите все с добавлением шума величиной 1 Вольт. 11. Ставим две частоты, отличающийся на 100 Гц – 10 В и 1 В. Добавляем шум величиной 3 вольта. Добиваемся таких параметров временного окна, чтобы оба сигнала были различимы на уровне шума. Зарисовываем картинку. Какова должна быть длительность временного окна чтобы различить сигнал с амплитудой в 10 раз меньше, чем уровень шума, если полоса частот сигнала (шум) – 1 кГц? А если полоса-100Гц, 10кГц?
Лабораторная работа №5 Методы интерполяции данных Цель лабораторной работы: В рамках данной лабораторной работы необходимо исследовать различные методы интерполяции данных. Теоретическая часть Интерполяция - отыскание промежуточных значений величины по некоторым известным её значениям. Линейная интерполяция (linear) — интерполяция алгебраическим двучленом P1(x) = ax + b функции f, заданной в двух точках x0 и x1 отрезка [a, b]. В случае, если заданы значения в нескольких точках, функция заменяется кусочно-линейной функцией. Применение Линейная интерполяция применяется для уплотнения таблиц. Формула линейной интерполяции является частным случаем интерполяционной формулы Лагранжа и интерполяционной формулы Ньютона. Интерполяция методом ближайшего соседа (nearest) — самый простой метод интерполяции функции одной или нескольких переменных. В качестве интерполированного значения выбирается ближайшее известное значение функции. Сплайн (spline) - кусочно-заданная функция, совпадающая с функциями более простой природы на каждом элементе разбиения своей области определения. Классический сплайн одной переменной строится так: область определения разбивается на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим полиномом. Максимальная степень из использованных полиномов называется степенью сплайна. Разность между степенью сплайна и получившейся гладкостью называется дефектом сплайна.
Интерполяционный многочлен Лагранжа (Lagrange) — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n + 1 пар чисел В простейшем случае (n = 1) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки
Этот пример показывает интерполяционный многочлен Лагранжа для четырёх точек (-9,5), (-4,2), (-1,-2) и (7,9), а также полиномы yj lj(x), каждый из которых проходит через одну из выделенных точек, и принимает нулевое значение в остальных xi
Лагранж предложил способ вычисления таких многочленов:
где базисные полиномы определяются по формуле:
lj (x) обладают следующими свойствами:
Отсюда следует, что L (x), как линейная комбинация lj (x), может иметь степень не больше n, и L (xj) = yj Полиномы Лагранжа используются для интерполяции, а также для численного интегрирования. Пусть для функции f (x) известны значения yj = f (xj) в некоторых точках. Тогда мы можем интерполировать эту функцию как
В частности,
Значения интегралов от lj не зависят от f (x), и их можно вычислить заранее, зная последовательность xi. РАБОЧЕЕ ЗАДАНИЕ
7. Запустить ВП 1D Interpolation.vi 8. Пронаблюдать влияние метода интерполяции на конечный результат. Объяснить полученные результаты. 9. Изменить набор данных и пронаблюдать влияние метода интерполяции как в пункте 2. Объяснить полученные результаты. 10. Запустить ВП Interpolation Solver.vi 11. Пронаблюдать влияние метода интерполяции на конечный результат. Объяснить полученные результаты. 12. Изменяя значение входных точек и точек интерполяции пронаблюдать влияние метода интерполяции на конечный результат. Объяснить полученные результаты. 13. Запустить ВП 2D Interpolation.vi 14. Пронаблюдать влияние метода интерполяции на конечный результат. Объяснить полученные результаты. Контрольные вопросы: 1. Почему при изображении спектра мощности на график выводится частоты только ниже частоты Найквиста? 2. Почему при некратных значениях N и частоты отсчетов спектр испытывает колебания? 3. Почему количество периодов синусоиды зависит от N? (кол-во точек FTT) 4. Какую роль играет частота оцифровки? 5. Чему равна частота Найквиста? 6. Чем отличаются цифровой и аналоговый сигналы? 7. Почему спектр реального и оцифрованного сигналов не всегда совпадают? 8. Что такое алиасинг? 9. Как вы объясните причины возникновения алиасинга? 10. Объясните на примерах, как используя теоремы Котельникова надо выбирать частоту оцифровки? 11. Можно ли, ничего не зная о спектре входного сигнала и работая только с оцифрованным выяснить, правильно ли выбрана частота оцифровки? Если можно то как? 12. Как влияет длительность окна на ширину спектра тонального спектра сигнала? 13. Как влияет тип временного окна на тип спектра сигнала? 14. Какой вид временного окна вы выберете, если вам необходимо выделить два сигнала с близкими частотами? 15. Какая роль спектральной характеристики окна. 16. Почему всегда используются временные окна? 17. Какова должна быть длительность временного окна, чтобы различить сигнал с амплитудой в 10 раз меньше, чем уровень шума, если полоса частот сигнала (шум) – 1 кГц?
Требования к оформлению отчёта Отчёт должен содержать: - титульный лист с наименованием учебного заведения, кафедры, курса, лабораторной работы, фамилией и подписью студента; - указание цели работы; - написать задачи; - описание объектов исследования; - результаты выполнения работы; - ответы на контрольные вопросы; - заключение, в котором приводится краткое перечисление выполненных действий, полученных результатов и сделанные из этих результатов выводы.
Лабораторная работа №1 Типовые сигналы и их спектры Цель лабораторной работы: В рамках данной лабораторной работы необходимо исследовать спектральные характеристики некоторых типовых сигналов, показать зависимость изменения спектральных характеристик этих сигналов от изменения их характеристик во временной области, а также рассмотреть различные виды модуляции сигналов.
Теоретическая часть Пусть дана функция s(t), описывающая исследуемый сигнал (процесс). Для данной функции существует прямое преобразование Фурье вида
если выполняются следующие условия:
Обратное преобразование Фурье задается следующим образом
Преобразование Фурье ставит в соответствие сигналу s(t), заданному во времени, его спектральную функцию (спектр) Спектр периодического сигнала является дискретным и представляет набор гармонических колебаний, в сумме составляющий исходный сигнал. Модуль спектральной функции
При создании систем передачи информации в большинстве случаев оказывается, что спектр исходного сигнала, подлежащего передаче, сосредоточен отнюдь не на тех частотах, которые эффективно пропускает имеющийся канал связи. Кроме того, очень часто необходимо в одном и том же канале связи передавать несколько сигналов одновременно. Одним из способов решения этой задачи является использование частотного разделения каналов, при котором разные сигналы занимают неперекрывающиеся полосы частот. Решение указанной проблемы достигается при использовании модуляции, сущность которой заключается в следующем. Формируется некоторое колебание (чаще всего гармоническое), называемое несущим колебанием или просто несущей и какой-либо из параметров этого колебания изменяется во времени пропорционально исходному сигналу. Исходный сигнал называют модулирующим, а результирующее колебание с изменяющимися во времени параметрами — модулированным сигналом. Обратный процесс — выделение модулирующего сигнала из модулированного колебания — называется демодуляцией.
Существуют различные виды модуляции:
Амплитудная модуляция сигнала - модуляция сигнала, изменяющая амплитуды несущей. При амплитудной модуляции высокий потенциал соответствует "единице", низкий - "нулю". Амплитудная модуляция соответствует переносу информации s(t) Þ U(t) при постоянных значениях параметров несущей частоты w и j.
Частотная модуляция сигнала - модуляция сигнала, в которой сигналы 0 и 1 передаются синусоидами, имеющими различные частоты. Частотная модуляция характеризуется линейной связью модулирующего сигнала с мгновенной частотой колебаний, при которой мгновенная частота колебаний образуется сложением частоты высокочастотного несущего колебания wo со значением амплитуды модулирующего сигнала с определенным коэффициентом пропорциональности:
w(t) = wo + k×s(t).
Фазовая модуляция - модуляция, в которой при изменении от "нуля" к "единице" и от "единицы" к "нулю" фаза синусоидальной несущей изменяется на 180 градусов. При фазовой модуляции значение фазового угла постоянной несущей частоты колебаний wo пропорционально амплитуде модулирующего сигнала s(t). Уравнение Фазовой модуляции сигнала определяется выражением
u(t) = Um cos[wot + k×s(t)], где k – коэффициент пропорциональности.
Рабочее задание
1. Запустить ВП Spectrum measurements.vi 2. Изменяя частоту входного сигнала пронаблюдать изменения спектра сигнала (логарифмическая и линейная шкалы) 3. Объяснить поведение спектра при значениях частот не кратных 10 4. Запустить ВП Amplitude spectrum (sim).vi 5. Отключить оконный фильтр (в окне window выбрать none) 6. Пронаблюдать амплитудные спектры для всех типов сигналов (синус, треугольник, пила, прямоугольный сигнал) на разных частотах. Объяснить полученные результаты
Рис. 1.1 Рабочий интерфейс ВП Spectrum measurements.vi
Рис. 1.2 Блок-диаграмма ВП Spectrum measurements.vi
Рис. 1.3 Рабочий интерфейс ВП Amplitude spectrum (sim).vi
Рис. 1.4 Блок-диаграмма ВП Amplitude spectrum (sim).vi
Лабораторная работа №2.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 500; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.151.141 (0.164 с.) |
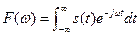 ,
, .
. .
. . При этом осуществляется переход из временной области в частотную. Преобразование Фурье является взаимно-однозначным, поэтому представление сигнала в частотной области содержит ровно столько же информации, сколько и исходный сигнал, заданный во временн о й области.
. При этом осуществляется переход из временной области в частотную. Преобразование Фурье является взаимно-однозначным, поэтому представление сигнала в частотной области содержит ровно столько же информации, сколько и исходный сигнал, заданный во временн о й области.




 будет записан правильно (по теореме Котельникова). Но т.к. помеха лежит выше частоты 22,05 кГц, то возникает алиасинг, и помеха «отразится» в нижнюю часто спектра, на частоту около 5 кГц. Если мы теперь попробуем пропустить полученный цифровой сигнал церез ЦАП и прослушать результат, то мы услышим на фоне музыки помеху на частоте 5 кГц. Таким образом. Помеха переместилась из неслышимой ультразвуковой области в слышимую область.
будет записан правильно (по теореме Котельникова). Но т.к. помеха лежит выше частоты 22,05 кГц, то возникает алиасинг, и помеха «отразится» в нижнюю часто спектра, на частоту около 5 кГц. Если мы теперь попробуем пропустить полученный цифровой сигнал церез ЦАП и прослушать результат, то мы услышим на фоне музыки помеху на частоте 5 кГц. Таким образом. Помеха переместилась из неслышимой ультразвуковой области в слышимую область. (2.1)
(2.1)
 (2.2)
(2.2) . Так как этот сигнал является и периодическим, его спектр должен быть дискретным с расстоянием между гармониками, равным
. Так как этот сигнал является и периодическим, его спектр должен быть дискретным с расстоянием между гармониками, равным 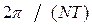 .
. гармоник).
гармоник). (2.3)
(2.3) (2.4)
(2.4) часто называют Фурье-образом последовательности
часто называют Фурье-образом последовательности  . Формула (2.3), представляет
. Формула (2.3), представляет  (2.5)
(2.5) принимает значения на интервале длины
принимает значения на интервале длины  , а
, а  определяется тем, какой вклад в суперпозицию вносит каждая синусоидальная компонента. Хотя
определяется тем, какой вклад в суперпозицию вносит каждая синусоидальная компонента. Хотя  до
до  , его можно заменить на любой сегмент длинны
, его можно заменить на любой сегмент длинны  . Преобразование Фурье ( 2.4 ) задает правило, вычисляющее
. Преобразование Фурье ( 2.4 ) задает правило, вычисляющее  , (2.6)
, (2.6) (2.7)
(2.7) и
и  - соответственно модуль и фаза Фурье-образа. Первую из них называют иногда амплитудным спектром, а вторую – фазовым спектром. Фурье-образ часто называют спектром Фурье или просто спектром.
- соответственно модуль и фаза Фурье-образа. Первую из них называют иногда амплитудным спектром, а вторую – фазовым спектром. Фурье-образ часто называют спектром Фурье или просто спектром.
 , т.е N - степень двойки. Это предположение чрезвычайно важно, так как на нем построена вся логика работы алгоритма. Разделим общую сумму на две: первая содержит слагаемые с четными индексами, вторая – с нечетными.
, т.е N - степень двойки. Это предположение чрезвычайно важно, так как на нем построена вся логика работы алгоритма. Разделим общую сумму на две: первая содержит слагаемые с четными индексами, вторая – с нечетными.
 из координат вида
из координат вида 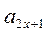 .
. положим k=j
положим k=j  запишем в виде
запишем в виде




 , где все xi различны, существует единственный многочлен L (x) степени не более n, для которого L (xi) = yi.
, где все xi различны, существует единственный многочлен L (x) степени не более n, для которого L (xi) = yi.