
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейные стационарные системы
Особое значение имеет класс систем, являющихся одновременно как линейными, так и стационарными. Наличие этих свойств позволяет представить системы в удобном виде. Более того, они играют ведущую роль в приложениях обработки сигналов. Класс линейных систем определяется с помощью принципа суперпозиции: если
где
где если где Учитывая свойство линейности и представление общей последовательности в виде линейной комбинации сдвинутых импульсов (1.2), можно заметить, что линейная система полностью определяется своей реакцией на сдвинутые импульсные последовательности. Более того, пусть
то По принципу суперпозиции (1.2) можно записать
Итак, мы получили, что реакция линейной системы на любую входную последовательность выражается в терминах откликов системы на сигналы Свойство стационарности влечет, что если
Как следствие этой формулы, отметим, что линейная стационарная система (ЛС-система) полностью определяется своей импульсной характеристикой Если отсчеты последовательности
Операция дискретной свертки строит последовательность
Порядок выполнения лабораторной работы: Запустить исполняемый файл Kotelnikov1.exe
Рис. 2.2 Рабочий интерфейс ВП Kotelnikov1.vi Рабочее задание: 1.Установить частоту сигнала = 4 Гц. Установить частоту оцифровки 9 Гц или больше. Убедиться, что спектр реального сигнала и оцифрованного сигнала совпадают. 2.Установить частоту сигнала = 4 Гц. Установить частоту оцифровки 30 герц. Убедиться, что фаза входного сигнала не влияет на его спектр. 3.Установить частоту оцифровки = 9 Гц, частоту сигнала = 4 Гц. Пронаблюдать изменение спектра оцифрованного сигнала при изменении фазы входного сигнала. Объяснить, почему при изменении фазы сигнала меняет спектр оцифрованного сигнала. 4.Установить частоту оцифровки = 6 Гц. Записать значения частоты оцифрованного сигнала. Объяснить получившиеся значения. 5.Установить частоту оцифрованного сигнала = 4 Гц. Пронаблюдать изменение спектра и амплитуды оцифрованного сигнала. 6.Установить частоту входного сигнала(FTone) =25 Гц. Установить частоту оцифровки (Fsam) = 10 Гц. Объяснить частоту оцифрованного сигнала. Объяснить влияние фазы на спектр и амплитуду оцифрованного сигнала.
Рабочее задание часть 2: 1. Запустить Kotelnikov2.exe 2. В управляющей панели переключаем Квантованный сигнал, Аналоговый сигнал и Ложную частоту в положение On. 3. Установить частоту аналогового сигнала = 50, Acq = 18, Начальное время = 0. 4. Изменяя частоту входного сигнала, пронаблюдать асциляцию частоты оцифрованного сигнала, возникающей при превышении частотой сигнала частоты Найквиста. 5. Убедиться в том, что частота оцифрованного сигнала всегда меньше частоты Найквиста. 6. Пронаблюдать, что частота оцифровывания сигнала и реального симметричны относительно частоты Найквиста, а при превышении эта закономерность исчезает. Объяснить почему.
Рис. 3.3 Рабочий интерфейс ВП Kotelnikov2.vi
* Частота Найквиста (Nyquist) - в цифровой обработке сигналов частота, равная половине частоты дискретизации. Из теоремы Котельникова следует, что при дискретизации сигнала полезную информацию будут нести только частоты ниже частоты Найквиста. Частоты выше частоты Найквиста являются зеркальным отображением нижних частот. Если спектр сигнала не имеет составляющих выше частоты Найквиста, то он может быть оцифрован и затем восстановлен без искажений. К примеру, в аудио компакт-дисках используется частота дискретизации 44100 герц. Частота Найквиста для них — 22050 герц, она ограничивает верхнюю полосу частот, до которой звук может быть воспроизведён без искажений.
Но это - теоретический предел. На практике есть некоторые нюансы. При оцифровке аналогового сигнала с широким спектром необходимо обеспечить срез спектра аналогового сигнала на частоте Найквиста при помощи фильтра очень высокого порядка, чтобы избежать зеркального отражения спектра для частот, лежащих выше частоты Найквиста. Практическая реализация такого фильтра весьма сложна, так как амплитудно-частотные характеристики фильтров имеют не прямоугольную, а колоколообразную форму и образуется некоторая полоса "затухания". Поэтому максимальную частоту спектра дискретизуемого сигнала принимают несколько ниже частоты Найквиста, чтобы обеспечить надёжное подавление фильтром спектра дискретизуемого сигнала.
Рис. 3.4 Правая половина разработанной блок-диаграммы ВП Kotelnikov2.vi
Рис. 3.5 Левая половина разработанной блок-диаграммы ВП Kotelnikov2.vi
Лабораторная работа №3. Исследование преобразования Фурье. Цель лабораторной работы: Изучение дискретного преобразования Фурье. Исследование изменение временных окон и спектрального разрешения сигнала. Теоретическая часть Разложению в ряд Фурье могут подвергаться периодические сигналы. При этом они представляются в виде суммы гармонических функций, либо комплексных экспонент с частотами, образующими арифметическую прогрессию. Чтобы такое разложение существовало, фрагмент сигнала длительностью в один период должен удовлетворять условиям Дирихле:
· не должно быть разрывов второго рода (с уходящими в бесконечность ветвями функции); · число разрывов первого рода (скачков) должно быть конечным; · число экстремумов должно быть конечным (в качестве примера функции, которая на конечном интервале имеет бесконечное число экстремумов, можно привести sin(1/x) в окрестностях нуля).
Дискретное преобразование Фурье, по возможности вычисляемое быстрыми методами, лежит в основе различных технологий спектрального анализа, предназначенных для исследования случайных процессов. Дело в том, что если анализируемый сигнал представляет собой случайный процесс, то простое вычисление его ДПФ обычно не представляет большого интереса, так как в результате получается лишь спектр единственной реализации процесса. Поэтому для спектрального анализа случайных сигналов необходимо использовать усреднение спектра. Такие методы, в которых используется только информация, извлеченная из самого входного сигнала, называются непараметрическими. Другой класс методов предполагает наличие некоторой статистической модели случайного сигнала. Процесс спектрального анализа в данном случае включает в себя определение параметров этой модели, и потому такие методы называются параметрическими.
Пусть последовательность отсчетов {x(k)} является периодической с периодом N:
Такая последовательность полностью описывается конечным набором чисел, в качестве которого можно взять произвольный фрагмент длиной N, например {x(k)}, k=0,1,…,N-1. Поставленный в соответствие этой последовательности сигнал из смещенных по времени дельта-функций:
также, будет с периодическим с минимальным периодом NT. Так как сигнал (2.2) является дискретным, его спектр должен быть периодическим с периодом Итак, периодический дискретный сигнал имеет периодический дискретный спектр, который также описывается конечным набором из N чисел (один период спектра содержит
Одно из преимуществ частотного представления линейных стационарных систем заключается в том, что интерпретация их поведения получается довольно легко. Многие из последовательностей выражаются через интеграл Фурье вида , где Формулы (2.3) и (2.4) называют представлением, или преобразованием Фурье, а саму функцию
Где Фурье-образ – комплекснозначная функция от
Величины Свойства ДПФ N-членная последовательность N-точечное ДПФ
Заметим, что все свойства сформулирвоанны для конечных последовательностей x[n] и X[k], определенных на интервале [0; N-1]. Обе последовательности имеют нулевые отсчеты вне этого отрезка.
Стоит отметить, что нулевая гармоника является суммой значений сигнала.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 377; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.66.206 (0.031 с.) |
 и
и  - отклики системы на сигналы
- отклики системы на сигналы  и
и  , то систему называют линейной тогда и только тогда, когда
, то систему называют линейной тогда и только тогда, когда (1.1)
(1.1) – произвольная константа. Первое свойство называется аддитивностью, а второе – однородностью. Оба свойства можно записать одной формулой по принципу суперпозиции:
– произвольная константа. Первое свойство называется аддитивностью, а второе – однородностью. Оба свойства можно записать одной формулой по принципу суперпозиции: (1.2)
(1.2) - произвольные константы. Последнее соотношение легко может быть переписано для нескольких сигналов, а именно
- произвольные константы. Последнее соотношение легко может быть переписано для нескольких сигналов, а именно , то
, то  , (1.3)
, (1.3) - реакция системы на поданный сигнал
- реакция системы на поданный сигнал 
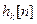 - реакция системы на
- реакция системы на  . Тогда согласно тождеству
. Тогда согласно тождеству (1.4)
(1.4) (1.5)
(1.5)
 (1.6)
(1.6) зависят как от
зависят как от  так и от
так и от 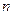 , и помощь оказываемая уравнением (1.6) при вычислениях, относительно не высока. Однако можно получить более полезный результат, если к свойству линейности добавить условие стационарности.
, и помощь оказываемая уравнением (1.6) при вычислениях, относительно не высока. Однако можно получить более полезный результат, если к свойству линейности добавить условие стационарности. - реакция системы на
- реакция системы на  (называемая импульсной характеристикой системы), то ее реакция на сигнал
(называемая импульсной характеристикой системы), то ее реакция на сигнал  . Опираясь на этот факт, уравнение (1.6) можно переписать в виде
. Опираясь на этот факт, уравнение (1.6) можно переписать в виде (1.7)
(1.7) в том смысле, что при известной последовательности
в том смысле, что при известной последовательности 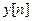 на любой поданный сигнал
на любой поданный сигнал 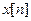 .
. (1.8)
(1.8)



 (2.1)
(2.1)
 (2.2)
(2.2) . Так как этот сигнал является и периодическим, его спектр должен быть дискретным с расстоянием между гармониками, равным
. Так как этот сигнал является и периодическим, его спектр должен быть дискретным с расстоянием между гармониками, равным 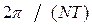 .
. гармоник).
гармоник). (2.3)
(2.3) (2.4)
(2.4) часто называют Фурье-образом последовательности
часто называют Фурье-образом последовательности  . Формула (2.3), представляет
. Формула (2.3), представляет  (2.5)
(2.5)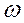 принимает значения на интервале длины
принимает значения на интервале длины  , а
, а  определяется тем, какой вклад в суперпозицию вносит каждая синусоидальная компонента. Хотя
определяется тем, какой вклад в суперпозицию вносит каждая синусоидальная компонента. Хотя  до
до  , его можно заменить на любой сегмент длинны
, его можно заменить на любой сегмент длинны  . Преобразование Фурье ( 2.4 ) задает правило, вычисляющее
. Преобразование Фурье ( 2.4 ) задает правило, вычисляющее  , (2.6)
, (2.6) (2.7)
(2.7) и
и  - соответственно модуль и фаза Фурье-образа. Первую из них называют иногда амплитудным спектром, а вторую – фазовым спектром. Фурье-образ часто называют спектром Фурье или просто спектром.
- соответственно модуль и фаза Фурье-образа. Первую из них называют иногда амплитудным спектром, а вторую – фазовым спектром. Фурье-образ часто называют спектром Фурье или просто спектром.



