
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Резистивные делители тока и напряженияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Резистивные делители широко применяются в электрических цепях приборов. Схемы простейших делителей тока и напряжения приведены на рис. 2-5, а, б. Коэффициенты передачи, или коэффициенты деления, делителей равны
Рис. 2-5
С учетом сопротивлений источников и нагрузок выходной ток и выходное напряжение определяются формулами:
Коэффициент деления тока не зависит от сопротивления цепи, включенной последовательно с делителем, т.е. от сопротивления источника. При постоянных сопротивлениях делителя и нагрузки изменение коэффициента деления учитывается формулами:
Или, учитывая, что выходные сопротивления делителей составляют
коэффициенты деления можно представить в виде:
Из приведенных формул легко определить погрешность делителей при изменении сопротивления нагрузки или выходных сопротивлений делителей. Однако, даже если нагрузки остаются неизменными, включение нагрузок, имеющих сопротивления, сравнимые с выходными сопротивлениями делителей, крайне нежелательно, так как это приводит к существенному возрастанию погрешностей делителей под влиянием внешних факторов. Для ненагруженных делителей погрешности от влияния внешних факторов пренебрежимо малы, так как используемые в них резисторы идентичны и отношение их сопротивлений является инвариантной величиной. По-разному влияют внешние воздействия на сопротивления делителя и нагрузки, так как последние выполняются из различных материалов, и поэтому возрастают соответствующие погрешности. Полагая, что под действием температуры относительная погрешность резисторов делителя составляет g R, а относительная погрешность сопротивления нагрузки g R н можно написать следующие выражения для погрешностей коэффициентов деления:
Если на вход резистивного делителя подается переменное напряжение достаточно высокой частоты или напряжение, содержащее высокочастотные гармоники, то необходимо учитывать реактивные составляющие сопротивлений, входящих в делитель резисторов. Для того чтобы избежать частотной погрешности, должно выполняться следующее условие: R 1/ R 2 = L 1 /L 2 =C 2 /C 1, где L 1, L 2, C 1и C 2– параметры эквивалентной схемы резисторов. Влияние индуктивной составляющей комплексного сопротивления обычно невелико, что объясняется соответствующей конструкцией непроволочных резисторов и бифилярной намоткой высокочастотных проволочных резисторов. Емкостная же составляющая сопротивления может вносить заметную погрешность. Эту погрешность можно исключить, выравнивая постоянные времени резисторов делителя, для чего подбирают небольшие конденсаторы, включаемые параллельно резисторам. Использование подобной емкостной коррекции позволяет снизить частотную погрешность делителей до десятых долей процента для частот звукового диапазона при применении микропроволочных резисторов типа МВСГ и для частот вплоть до нескольких десятков мегагерц при использовании непроволочных резисторов. Дальнейшее снижение частотной погрешности возможно при применении более сложных схем частотной коррекции. Существенно увеличиваются частотные погрешности делителей при включении сопротивления нагрузки. В рабочем диапазоне частот, где резисторы делителя имеют чисто активные сопротивления, частотные погрешности, вызванные реактивными составляющими сопротивлений нагрузок, определяются формулами:
если считать, как это и бывает в большинстве случаев, что нагрузка делителя тока имеет индуктивную составляющую, а нагрузка делителя напряжения – емкостную. Многоступенчатые резистивные делители напряжения и тока приведены на рис. 2-5, г и д, где в качестве примеров указаны значения сопротивлений. Подобные схемы используются для переключения пределов амперметров и аналоговых электронных вольтметров. Особую роль играют многоступенчатые делители с многозначными регулируемыми коэффициентами деления, используемые в современных цифровых приборах и компенсаторах ручного уравновешивания. В качестве примера на рис. 2-6 показан трехзначный делитель, который может выполняться как с ручным, так и с автоматическим изменением коэффициента деления. Принцип действия делителя поясняется рис. 2-6, а. Делитель состоит из идентичных резисторов, по которым перемещаются два механически соединенных, но электрически изолированных движка. Часть резистора, к которой приложено напряжение, показана штриховкой; та часть резистора, с которой снимается напряжение, показана более густой штриховкой.На рис. 2-6, б, в представлены построенные на этом принципе делитель с ручным управлением (при указанном положении движков U ВЫХ = 0,120· U ВХ) и с автоматическим управлением путем замыкания и размыкания соответствующих контактов реле (при указанном положении контактов U ВЫХ = 0,538 U ВХ).
Рис. 2-6
Число знаков коэффициента деления определяется возможным диапазоном сопротивлений резисторов, поскольку, как видно из рис. 2-6, в,для того чтобы не сказывались остаточные параметры ключей, то сопротивление из них, которое меньше, должно быть на 1–2 порядка больше сопротивления r к замкнутого ключа, а то, которое больше на 2–3 порядка меньше сопротивления R к разомкнутого ключа. Если предположить, что r к = 0,01 Ом, а R к = 108 Ом, то можно реализовать пятизначный делитель, в котором коэффициент деления будет иметь погрешность, не превышающую последнего знака. Анализируя различные схемы делителей, нужно обратить внимание на следующие характеристики: постоянство входного сопротивления, постоянство выходного сопротивления, наличие общей шины между цепями входного и выходного напряжения, влияние остаточных параметров ключей, число используемых в делителе номиналов резисторов. В современных цифровых приборах применяются лестничные делители тока и напряжения на выполненных по интегральной технологии матрицах резисторов, содержащих всего два номинала резисторов R и 2 R. Схемы таких делителей показаны на рис. 2-7. В делителе напряжения (рис. 2-7, a) используется один источник напряжения и усилитель с бесконечно большим входным сопротивлением, с выхода которого снимается нужная часть входного сигнала. В делителе тока (рис. 2-7, б) используется несколько идентичных источников тока и суммирующий усилитель с бесконечно малым входным сопротивлением. На рис. 2-7, в и г показаны эквивалентные схемы того и другого делителя при замыкании (n–2)-го ключа в положение 1. а) б)
Рис. 2-7
Резистивная матрица имеет постоянное выходное сопротивление R вых =R. Коэффициенты деления делителя тока и делителя напряжения составляют:
где a i принимают значения 0 и 1 в зависимости от положения ключей. Лучшие делители имеют до 16 разрядов, погрешность линейности ±0,002%, температурную погрешность ±0,0007% на 1 К.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-22; просмотров: 806; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.01 с.) |

 ;
;  и определяются отношением сопротивлений входящих в них резисторов, поэтому точность коэффициента деления определяется не точностью самих сопротивлений резисторов, а лишь точностью поддержания их отношения. Приведенные выражения справедливы для случая, когда можно пренебречь внутренними сопротивлениями источников и нагрузок, полагая, что для делителя напряжения R H = ¥, а для делителя тока R Н ® 0.
и определяются отношением сопротивлений входящих в них резисторов, поэтому точность коэффициента деления определяется не точностью самих сопротивлений резисторов, а лишь точностью поддержания их отношения. Приведенные выражения справедливы для случая, когда можно пренебречь внутренними сопротивлениями источников и нагрузок, полагая, что для делителя напряжения R H = ¥, а для делителя тока R Н ® 0.
 ;
;  .
.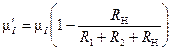 ;
;  .
. ,
,  ,
, ;
;  .
. ;
;  .
. ;
;  ,
,




 ,
,


