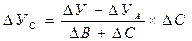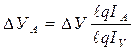Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Способи пропорційного ділення і часткової участіСодержание книги
Поиск на нашем сайте
Використання способу пропорційного ділення в адитивних моделях типу У = А + В + С має наступний алгоритм розрахунку впливу факторів на зміну результативного показника:
; (5.80)
. (5.81)
При застосуванні способу часткової участі спочатку визначається частка кожного фактора у загальній сумі їх приростів, яка потім множиться на загальну зміну результативного показника:
; (5.82)
; (5.83)
(5.84) Більш складною є методична схема розрахунків для змішаних моделей. Розглянемо, наприклад, взаємозв’язок факторів на рисунку 5.1. Розрахунки впливу факторів А, В і С на зміну результативного показника У виконуються в такій послідовності: 1. Визначаються величини впливу факторів Х1, Х2 і Х3 на зміну результативного показника У (DУХ1; DУХ2; DУХ3) за допомогою одного із способів детермінованого факторного аналізу.
другого рівня Рис. 5.1. Схема факторного аналізу
2. Визначаються величини впливу факторів А, В і С на зміну показника Х2 (DХ2А; DХ2В; DХ2С) за допомогою одного із способів детермінованого факторного аналізу. 3. Визначається допоміжний коефіцієнт за формулою К = DУХ2 ¸ DХ2 = DУХ2 ¸ (DХ2А + DХ2В + DХ2С). (5.85) 4. Визначається вплив факторів А, В і С на зміну результативного показника У: DУА = К х DХ2А; (5.86) DУВ = К х DХ2В; (5.87) DУС = К х DХ2С. (5.88)
Інтегральний спосіб
Способи детермінованого факторного аналізу, які ґрунтуються на принципі елімінування, мають спільний суттєвий недолік: при їх використанні виходять із того, що фактори змінюються незалежно один від одного. Однак, в дійсності, зміна одного фактора породжує зміну всіх інших, фактори змінюються одночасно, у взаємному зв’язкові. Від цієї взаємодії утворюється додаткова зміна результативного показника, яка при застосуванні способів елімінування приєднується до впливу одного з факторів (як правило, до останнього) на зміну результативного показника. Як наслідок дещо знижується результат впливу тих факторів, заміна (підстановка) яких проводиться раніше, за рахунок завищення результату останньої підстановки. Отже, величина впливу факторів на зміну результативного показника змінюється залежно від місця того чи іншого фактора в детермінованій факторній моделі. Проблему утворення додаткової зміни результативного показника від взаємодії факторів розглянемо на умовному прикладі. Нехай У = А х В – двофакторна мультиплікативна модель. Загальна зміна результативного показника (DУ) дорівнює сумі змін за рахунок факторів А (DУА) і В (DУВ): DУ = DУА + DУВ. (5.89) Насправді при розкладанні загальної зміни результативного показника отримують не два, а три компоненти: DУ = У1 – У0 = А1хВ1 – А0хВ0 = (А0 + DА) х (В0 +DВ) – А0хВ0 = = А0хВ0 + А0хDВ + DАхВ0 + DАхDВ – А0хВ0 = = DАхВ0 + DВхА0 + DАхDВ. (5.90) Останній параметр рівняння (DАхDВ) називається «нерозподіленим залишком», економічний зміст якого полягає у представленні сукупного одночасного впливу двох факторів А і В на зміну результативного показника У. Цей параметр, згідно із способами елімінування, не має права на самостійне існування й приєднується до величини впливу останнього фактора моделі. З метою подолання зазначених недоліків у детермінованому факторному аналізі використовуються більш досконалі способи: інтегральний і логарифмічний. Інтегральний спосіб дозволяє уникнути недоліків, властивих способам елімінування, тому що в цьому разі результати факторного аналізу не залежать від місця розташування факторів у моделі, а додаткова зміна результативного показника, яка утворилася від взаємодії факторів, розподіляється між ними пропорційно ізольованому їх впливу на результативний показник. При застосуванні інтегрального способу користуються робочими формулами для розрахунків, які наводяться у спеціальній літературі з економічного аналізу. 1. Для мультиплікативних моделей: а) У = А х В. (5.91) DУА = DА х В0 + ½ DА х DВ; (5.92) DУВ = DВ х А0 + ½ DА х DВ. (5.93) б) У = А х В х С. (5.94) DУА = ½DА х (В0 х С1 + В1 х С0) + ⅓ DА х DВ х DС; (5.95) DУВ = ½DВ х (А0 х С1 + А1 х С0) + ⅓ DА х DВ х DС; (5.96) DУС = ½DС х (А0 х В1 + А1 х В0) + ⅓ DА х DВ х DС. (5.97) 2. Для кратних моделей:
DУВ = DУ - DУА . (5.100)
3. Для змішаних моделей:
; (5.102)
; (5.103)
. (5.104)
Логарифмічний спосіб
Результати розрахунків логарифмічним способом, як і при інтегральному способі, не залежать від місця розташування факторів у моделі. Порівняно з інтегральним способом спосіб логарифмування забезпечує більшу точність розрахунку впливу факторів на зміну результативного показника. Якщо при інтегральному способі додаткова зміна результативного показника, що виникла від взаємодії факторів, розподіляється порівну між ними, то логарифмічний спосіб величину сукупної дії факторів розподіляє пропорційно частці ізольованого впливу кожного фактора на зміну результативного показника. Методична схема розрахунків для трифакторної мультиплікативної моделі: У = А х В х С. (5.105) Прологарифмуємо обидві частини рівності: ℓqУ = ℓqА + ℓqВ + ℓqС. (5.106) Проведемо заміну абсолютних значень показників на їхні індекси:
, (5.107)
або ℓqІУ = ℓqІА +ℓqІВ + ℓqІС. (5.108) Розділивши обидві частини рівності на ℓqІУ і помноживши на DУ, одержимо:
. (5.109)
Звідси вплив факторів на зміну результативного показника визначається наступним чином:
; (5.110)
; (5.111)
. (5.112)
Отже, загальна зміна результативного показника розподіляється між факторами пропорційно відношенням логарифмів (десяткових або натуральних) індексів факторних показників до логарифма індексу результативного показника. Розглянуті способи детермінованого факторного аналізу забезпечують можливість досліджувати будь-які показники діяльності підприємства окремо або в комплексі. Однак навіть під час аналізу окремих показників дуже рідко користуються тільки одним із розглянутих методів. Для досягнення кінцевої мети аналізу необхідно застосовувати комбінацію різних прийомів та способів.
КОНТРОЛЬНІ ПИТАННЯ
1. Назвати способи вимірювання впливу факторів у детермінованому факторному аналізі. 2. Описати методичні схеми застосування способів детермінованого факторного аналізу: способу ланцюгових підстановок, способу абсолютних різниць, способу відносних різниць. 3. В чому полягає індексний спосіб вимірювання впливу факторів у детермінованому факторному аналізі? 4. Як використовуються способи пропорційного ділення і часткової участі. 5. Схарактеризувати переваги й недоліки, пояснити алгоритм застосування інтегрального способу і логарифмічного способу. ТЕМА 6
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 352; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.13.196 (0.006 с.) |

 ; (5.79)
; (5.79)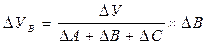
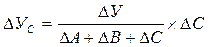





 першого рівня
першого рівня
 (5.98)
(5.98)

 DУА= ℓn; (5.99)
DУА= ℓn; (5.99) . (5.101)
. (5.101)