
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел числовой последовательности.Стр 1 из 6Следующая ⇒
Функция.
Определение 13.3. Если каждому элементу х множества Х (называемого областью определения функции) по определенному закону ставится в соответствие единственный элемент у множества Y, то подобное отображение называется функцией, определенной на множестве Х со значениями в множестве Y. При этом х называется независимой переменной, или аргументом, а у = f(x) – зависимой переменной, или функцией.
Замечание. Мы будем рассматривать только однозначные функции (в отличие от многозначных функций, для которых одному значению х может соответствовать более одного значения у).
Способы задания функции: 1) табличный 2) графический 3) аналитический.
Определение 13.4. Если у=F(u) является функцией от u, a u=φ(x) – функцией от х, то у = F [ φ(x)] называется сложной функцией или функцией от функции. Основные элементарные функции. 1. Степенная функция у = хα, 2. Показательная функция у = ах, a > 0, a 3. Логарифмическая функция y =log ax, a > 0, a 4. Тригонометрические функции: y = sin x, y = cos x, y = tg x, y = ctg x, y = sec x, y = cosec x. 5. Обратные тригонометрические функции: y = arcsin x, y = arсcos x, y = arctg x, y = arcctg x, y = arcsec x, y = arccosec x.
Определение 13.5. Элементарной функцией y = f(x) называется функция, заданная с помощью основных элементарных функций и постоянных с помощью конечного числа арифметических операций и взятия функции от функции.
Определение 13.6. Если для функции у = f(х) можно определить функцию х = g(у), ставящую в соответствие каждому значению функции у = f(x) значение ее аргумента х, то функция у = g(x) называется обратной функцией к у = f(x) и обозначается y = f –1(x).
Пределы функций. Определим понятие окрестности точки х 0 как множество значений х, являющихся решениями неравенства 0<| x - x 0| < δ, где δ > 0 – некоторое число. Само значение х 0 может включаться в окрестность или не включаться в нее (в этом случае окрестность называется проколотой). Пусть функция у = f(x) определена в некоторой окрестности точки х 0.
Определение 13.7. Число А называется пределом функции у = f(x) при х, стремящемся к х 0, если Обозначение:
Замечание. Для существования предела функции в точке х 0 не требуется, чтобы функция была определена в самой этой точке.
Примеры.
Определение 13.8. Функция у = f(x) имеет бесконечный предел при х, стремящемуся к х 0 (стремится к бесконечности, является бесконечно большой), если Обозначение:
Определение 13.9. Число А называется пределом функции y = f(x) на бесконечности, если
Замечание. Бесконечный предел функции на бесконечности можно определить по аналогии с определением 13.8.
Определение 13.10. Функция у = f(x) называется ограниченной в некоторой области значений х, если существует число М >0 такое, что | f(x)|<M для всех значений х, принадлежащих рассматриваемой области.
Свойства пределов.
1.Если существует Доказательство. Так как для любого ε существует такое δ, что | f(x) - A | < ε при | x - x0 | < δ, то при этом | f(x)| < |A | + ε, то есть функция ограничена в рассматриваемой окрестности. 2. Функция не может иметь двух различных пределов при х, стремящемуся к одному и тому же значению. Доказательство. Пусть А и В – пределы f(x) при х→х0. Выберем ε < | A-B |. Тогда существует такое δ1, что | f(x)-A |<ε/2 при | x - x0 | < δ1, и такое δ2, что |f (x)-B |<ε/2 при | x - x0 | < δ2. Если выбрать в качестве δ меньшее из чисел δ1 и δ2, то значения функции f(x) для аргументов, лежащих в δ – окрестности х 0, должны одновременно находиться в двух непересекающихся окрестностях, что невозможно. Утверждение доказано.
Доказательство. Достаточно выбрать ε=| A |/2. Тогда для х из некоторой окрестности х 0 | f(x)-A | < | A |/2, то есть А /2 < f(x) < 3 A /2 при A > 0 и 3 A /2 < f(x) < A /2 при A < 0. Следовательно, в выбранной окрестности f(x) сохраняет постоянный знак.
Односторонние пределы.
Определение 13.11. Число А называется пределом функции у = f(x) при х, стремящемся к х0 слева (справа), если Обозначения:
Теорема 13.1(второе определение предела). Функция y=f(x) имеет при х, стремящемся к х 0, предел, равный А, в том и только в том случае, если оба ее односторонних предела в этой точке существуют и равны А. Доказательство. 1) Если 1) Если Замечание. Поскольку доказана эквивалентность требований, содержащихся в определении предела 13.7 и условия существования и равенства односторонних пределов, это условие можно считать вторым определением предела.
Лекция 14. Бесконечно малые функции и их свойства. Основные теоремы о пределах. Замечательные пределы. Натуральный логарифм и гиперболические функции.
Определение 14.1. Функция у=α(х) называется бесконечно малой при х→х0, если Свойства бесконечно малых.
Доказательство. Если α(х) и β(х) – бесконечно малые при х→х0, то существуют δ1 и δ2 такие, что | α(x)|<ε/2 и |β(x)|<ε/2 для выбранного значения ε. Тогда | α(x)+β(x)|≤|α(x)|+|β(x)|<ε, то есть |(α(x)+β(x))-0|<ε. Следовательно, Замечание. Отсюда следует, что сумма любого конечного числа бесконечно малых есть бесконечно малая.
Доказательство. Выберем число М такое, что | f(x)|<M при | x-x0|< δ1, и найдем такое δ2, что | α(x)|<ε/M при | x-x0 |<δ2. Тогда, если выбрать в качестве δ меньшее из чисел δ1 и δ2, |α (x)·f(x)|<M·ε/M=ε, то есть α(х)·f(x) – бесконечно малая. Следствие 1. Произведение бесконечно малой на конечное число есть бесконечно малая. Следствие 2. Произведение двух или нескольких бесконечно малых есть бесконечно малая. Следствие 3. Линейная комбинация бесконечно малых есть бесконечно малая.
Доказательство. 1) Пусть 2) Пусть f(x)=A+α(x). Тогда Замечание. Тем самым получено еще одно определение предела, эквивалентное двум предыдущим.
B C
A x Используя соответствующие геометрические формулы для площадей фигур, получим отсюдa, что Тогда Замечание. Доказанное справедливо и при x< 0. Доказательство. 1. Докажем сначала, что последовательность
возрастающая переменная величина при возрастающем n. С другой стороны,
Следовательно, 2. Докажем, что а) Пусть
Следовательно, по теореме 14.4 б) Если Пример.
Бесконечно большие функции. Определение 15.1. Функция f(x) называется бесконечно большой при х
Для бесконечно больших можно ввести такую же систему классификации, как и для бесконечно малых, а именно: 1. Бесконечно большие f(x ) и g(x ) считаются величинами одного порядка, если
2. Если 3. Бесконечно большая f(x ) называется величиной k -го порядка относительно бесконечно большой g(x ), если Замечание. Отметим, что ах – бесконечно большая (при а >1 и х Теорема 15.1. Если α(х ) – бесконечно малая при х→х0, то 1/ α(х ) – бесконечно большая при х→х0 . Доказательство. Докажем, что |1/ α(x )|> M. Значит, Лекция 16. Непрерывность функции в точке. Локальные свойства непрерывных функций. Непрерывность сложной и обратной функций. Непрерывность элементарных функций. Точки разрыва функций и их классификация. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, промежуточные значения. Определение 16.1. Функция y=f(x ) называется непрерывной в точке х0, если
Замечание. Из этого определения следует, во-первых, что функция определена при х = = х0, и во-вторых, что при х→х0 существует конечный предел функции. Примеры. 1. 2. 3.
4. 5. Свойства функций, непрерывных на отрезке. Определение 16.6. Функция y=f(x ) называется непрерывной на отрезке [ ab ], если она непрерывна в каждой точке этого отрезка (при этом f(a ) и f(b ) равны соответствующим односторонним пределам). Теорема 16.1. Функция f(x ), непрерывная на отрезке [ ab ], ограничена на нем. Доказательство. По 1-му свойству предела существует окрестность точки х = а, в которой f(x ) ограничена, то есть существуют числа m 0 и М0: m0<f(x)<M0 в рассматриваемой окрестности. Выберем точку в правой части этой окрестности и рассмотрим окрестность этой точки, в которой f(x) тоже ограничена. Продолжим эту процедуру до тех пор, пока весь отрезок [ ab ] не будет покрыт системой из n окрестностей, причем для каждой i -й окрестности mi<f(x)<Mi. Следовательно, для любого х, принадлежащего отрезку [ ab ], верно неравенство: m<f(x)<M, где m =min( mi ), M =max( Mi). Значит, f(x) ограничена на [ ab ]. Замечание 2. Можно доказать, что всякое непустое ограниченное сверху (снизу) числовое множество имеет верхнюю (нижнюю) грань. Следовательно, верхняя и нижняя грань существует для значений функции, ограниченной на отрезке. Теорема 16.2. Если функция у=f(x ) определена и непрерывна на отрезке [ ab ], то она достигает на нем своей верхней и нижней грани. Доказательство. Ограниченность f(x) на [ ab ] следует из теоремы 16.1. Пусть М=sup f ( x ). Предположим, что f(x)<M на [ ab ], и рассмотрим вспомогательную функцию
g(x ) Теорема 16.3. Если функция y=f(x) непрерывна на отрезке [ ab ] и f(a)=A, f(b)=B, то для любого числа С, заключенного между А и В, найдется х 0 Доказательство. Пусть для определенности A<C<B. Найдем середину отрезка [ ab ]: х =(а+в) /2. Если при этом f(x)=C, то искомое значение х 0 найдено. В противном случае выберем ту половину отрезка, на концах которой значения f(x ) лежат по разные стороны С, и обозначим ее концы а 1 и b 1. Будем продолжать эту процедуру (деления отрезка пополам и выбора соответствующей половины). Тогда либо через конечное число шагов значение функции в середине очередного отрезка станет равно С, либо мы получим две последовательности ({ an }- начальных точек выбранных отрезков и { bn }- их конечных точек), имеющие своими пределами одну и ту же общую для всех отрезков точку х 0. Тогда в силу непрерывности f(x ) Но, поскольку отрезки выбирались так, что f(an) < C < f(bn ), получим, что
Следствие. Доказательство.
1) Если для y=f(x) существует 2) Пусть y=f(x ) дифференцируема при х=х0, то есть ее приращение имеет вид (17.2). Тогда Следствие. Дифференциал функции можно представить в виде Теорема 17.2. Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке. Доказательство. Из формулы (17.2) следует, что Замечание. Обратное утверждение неверно, то есть из непрерывности функции не следует ее дифференцируемость. Например, y = |x | непрерывна при х = 0, но не дифференцируема в этой точке. Линеаризация функции. Так как истинное значение приращения функции отличается от ее дифференциала на бесконечно малую более высокого порядка, чем Δ х, при приближенных вычислениях можно заменять Δ у на dy, то есть считать, что f(x0 + Δx) ≈ f(x0) + dy = f(x0) + f`(x0)(x -x0 ). При этом функция f(x ) для значений х, близких к х0, приближенно заменяется линейной функцией. Эта операция называется линеаризацией функции. Пример. Найдем приближенное значение
Лекция 18. Свойства производной (правила дифференцирования). Производная сложной и обратной функций. Инвариантность формы дифференциала. Таблица производных, логарифмическое дифференцирование. Дифференцирование функций, заданных параметрически.
Правила дифференцирования. Пусть при рассматриваемых значениях х существуют производные функций f(x ) и g(x ), то есть эти функции являются дифференцируемыми при данных значениях аргумента. Сформулируем и докажем некоторые свойства производных. 1. Доказательство.
2. Доказательство. 3. Доказательство.
4. Если g(x)≠ 0, то Доказательство.
Доказательство. Так как
Доказательство.
Инвариантность формы дифференциала. Найдем выражение для дифференциала сложной функции. Пусть y=f(u), u=φ(x ), то есть y=f(φ(x)). Тогда Производные основных элементарных функций. Примеры. 1. 2. = Пример. х = а (1 – cos t ), y = a ( t – sin t ) – параметрические уравнения кривой, называемой циклоидой. Найдем у΄(х): х΄(t) = a sin t, y΄(t) = a (1-cos t ),
Лекция 19. Точки экстремума функции. Определение 19.4. Точка х0 называется точкой максимума (минимума) функции y = =f(x), если f(x) ≤ f(x0) (f(x) ≥ f(x0)) для всех х из некоторой δ-окрестности точки х0. Определение 19.5. Точки максимума и минимума функции называются ее точками экстремума.
Примеры.
Теорема 19.1 (теорема Ферма). Если функция y = f(x) определена в некоторой окрестности точки х0, принимает в этой точке наибольшее (наименьшее) в рассматриваемой окрестности значение и имеет в точке х0 производную, то f′(x0)= 0.
Доказательство.Пусть f(x0) – наибольшее значение функции, то есть для любой точки выбранной окрестности выполняется неравенство f(x) ≤ f(x0). Тогда, если x < x0, Переходя к пределу в полученных неравенствах, находим, что из первого из них следует, что f′(x0) ≥ 0, а из второго – что f′(x0) ≤ 0. Следовательно, f′(x0) = 0. Замечание. В теореме Ферма важно, что х0 – внутренняя точка для данного промежутка. Например, функция y = x, рассматриваемая на отрезке [0;1], принимает наибольшее и наименьшее значения соответственно при х = 1 и х = 0, но ее производная в этих точках в ноль не обращается.
Теорема 19.2 (теорема Ролля). Если функция y = f(x) 1) непрерывна на отрезке [ ab ]; 2) дифференцируема во всех внутренних точках этого отрезка; 3) принимает равные значения на концах этого отрезка, то есть f(a) = f(b), то внутри интервала (ab) существует по крайней мере одна точка х = с, a < c < b, такая, что f′(c) = 0. Доказательство. Пусть M и m – наибольшее и наименьшее значения f(x) на [ ab ]. Тогда, если m = M, то f(x) = m = M – постоянная функция, и f′(x)=0 для любой точки отрезка [ ab ]. Если же m<M, то по теореме 16.2 хотя бы одно из значений m или M достигается во внутренней точке с отрезка [ ab ] (так как на концах отрезка функция принимает равные значения). Тогда по теореме Ферма f′(c) = 0.
Замечание 1. В теореме Ролля существенно выполнение всех трех условий. Приведем примеры функций, для каждой из которых не выполняется только одно из условий теоремы, и в результате не существует такой точки, в которой производная функции равна нулю.
0 1 х 0 х -1 0 1 х
Рис. 1. Рис. 2. Рис. 3. Действительно, у функции, график которой изображен на рис. 1, f(0)=f( 1 )=0, но х =1 – точка разрыва, то есть не выполнено первое условие теоремы Ролля. Функция, график которой представлен на рис.2, не дифференцируема при х = 0, а для третьей функции f(- 1 )≠f( 1 ). Замечание 2. Геометрический смысл теоремы Ролля: на графике рассматриваемой функции найдется по крайней мере одна точка, касательная в которой параллельна оси абсцисс.
Лекция 20. Лекция 21. Лекция 23. Исследование выпуклости функции. Точки перегиба, их нахождение. Асимптоты функций. Общая схема исследования функции и построения ее графика. Определение 23.1. Кривая называется выпуклой (обращенной выпуклостью вверх) на интервале (ab), если все точки кривой лежат ниже любой ее касательной на этом интервале. Определение 23.2.. Кривая называется вогнутой (обращенной выпуклостью вниз) на интервале (ab), если все точки кривой лежат выше любой ее касательной на этом интервале.
А В С
Например, кривая, изображенная на рисунке, выпукла на интервале (ВС) и вогнута на интервале (АВ). Теорема 23.1. Если f ′′(x) < 0 во всех точках интервала (ab), то кривая y = f(x) выпукла на этом интервале. Если f ′′(x) > 0 во всех точках интервала (ab), то кривая y = f(x) вогнутаа на этом интервале.
а x0 b
Выберем на интервале (ab) произвольную точку х = х0 и докажем, что все точки кривой на этом интервале лежат ниже проведенной в точке с абсциссой х0 касательной, то есть ордината любой точки кривой на рассматриваемом интервале меньше ординаты касательной. Уравнение кривой имеет вид y = f(x), а уравнение касательной при х = х0:
Тогда (здесь с1 – между х 0 и с). Пусть x > x0. Тогда x0 < c1 < c < x, то есть c – x0 > 0, x – x0 > 0, f ′′(c1) < 0, поэтому Второе утверждение теоремы доказывается аналогичным образом. Определение 23.3. Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой, называется точкой перегиба. Замечание. Если в точке перегиба существует касательная к кривой, то в этой точке она пересекает кривую, потому что по одну сторону от данной точки кривая проходит выше касательной, а по другую – ниже. Теорема 23.2 (необходимое условие точки перегиба). Если в точке x0 перегиба кривой, являющейся графиком функции y = f(x), существует вторая производная f ′′(x), то f ′′(x0) = 0. Доказательство. Так как при х = х0 Теорема 23.3 (достаточное условие точек перегиба). Если функция y = f(x) дифференцируема в точке х0, дважды дифференцируема в проколотой окрестности этой точки и f ′′(x) меняет знак при х = х0, то х0 – точка перегиба. Доказательство. Воспользовавшись формулой (23.1), получим, что знак разности Замечание. Можно доказать, что если в условиях теоремы 22.5 критическая точка не является точкой экстремума, то она является точкой перегиба. Пример. Найдем интервалы выпуклости и вогнутости и точки перегиба функции y = x³ -6 x² + x – 12. y′ = 3 x ² - 12 x + 1, y′′ = 6 x – 12. y′′ = 0 при х = 2, y′′ < 0 при х < 2, y′′ > 0 при х > 2. Таким образом, график функции является выпуклым при х < 2, вогнутым при х > 2, а х = 2 – точка его перегиба. Асимптоты. Определение 23.4. Прямая называется асимптотой графика функции y = f(x), если расстояние от переменой точки этого графика до прямой стремится к нулю при удалении точки в бесконечность. Рассмотрим три вида асимптот и определим способы их нахождения. 1. Вертикальные асимптоты – прямые, задаваемые уравнениями вида х = а. В этом случае определение асимптоты подтверждается, если хотя бы один из односторонних пределов функции в точке а бесконечен. Пример. Вертикальной асимптотой графика функции y = 1/ x является прямая х = 0, то есть ось ординат. 2. Горизонтальные асимптоты – прямые вида у = а. Такие асимптоты имеет график функции, предел которой при
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 254; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.147.53 (0.197 с.) |
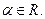
 1.
1.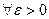
 такое, что | f(x) - A | < ε при | x - x0 | < δ.
такое, что | f(x) - A | < ε при | x - x0 | < δ.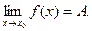 .
. Если |2 x +1-7| < ε, то |2 x - 6| < ε, | x - 3| < ε/2. Таким образом, если принять δ(ε) = ε/2, то выполнены все условия определения предела. Утверждение доказано.
Если |2 x +1-7| < ε, то |2 x - 6| < ε, | x - 3| < ε/2. Таким образом, если принять δ(ε) = ε/2, то выполнены все условия определения предела. Утверждение доказано. Заметим, что в проколотой окрестности х=2
Заметим, что в проколотой окрестности х=2  поэтому мы имеем право сократить дробь на (х - 2).
поэтому мы имеем право сократить дробь на (х - 2).
 такое, что | f(x)| > M при | x - x0 | < δ.
такое, что | f(x)| > M при | x - x0 | < δ.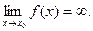
 при x > X (
при x > X (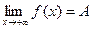 ), при x < -X (
), при x < -X ( ), при |x| > X (
), при |x| > X (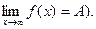
 , то существует окрестность точки х 0, в которой функция f(x) сохраняет постоянный знак (f(x)> 0, если A > 0, и f(x)<0, если A < 0).
, то существует окрестность точки х 0, в которой функция f(x) сохраняет постоянный знак (f(x)> 0, если A > 0, и f(x)<0, если A < 0).

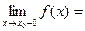

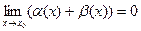 , то есть α(х)+β(х) – бесконечно малая.
, то есть α(х)+β(х) – бесконечно малая. при х→х0. Следовательно, f(x)=A+α(x).
при х→х0. Следовательно, f(x)=A+α(x). значит,
значит, 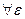 | f(x)-A |<ε при | x - x0 | < δ(ε). Cледовательно,
| f(x)-A |<ε при | x - x0 | < δ(ε). Cледовательно, 


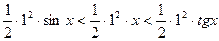 , или sin x < x <tg x. Разделив все части неравенства на sin x (при 0< x <π/2 sin x >0), запишем неравенство в виде:
, или sin x < x <tg x. Разделив все части неравенства на sin x (при 0< x <π/2 sin x >0), запишем неравенство в виде:  .
.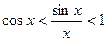 , и по теореме 14.4
, и по теореме 14.4 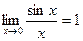 .
. при
при  имеет предел, заключенный между 2 и 3. По формуле бинома Ньютона
имеет предел, заключенный между 2 и 3. По формуле бинома Ньютона
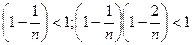 и т.д., поэтому
и т.д., поэтому
 - ограниченная и возрастающая величина, поэтому она имеет предел (см. теорему 14.6). Значение этого предела обозначается числом е .
- ограниченная и возрастающая величина, поэтому она имеет предел (см. теорему 14.6). Значение этого предела обозначается числом е .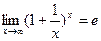 .
.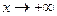 . Тогда
. Тогда 
 . При
. При 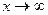


 то
то  и
и  Теорема доказана.
Теорема доказана.
 х0, если
х0, если
 .
. , то f(x ) считается бесконечно большой более высокого порядка, чем g(x).
, то f(x ) считается бесконечно большой более высокого порядка, чем g(x). 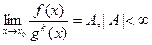 .
.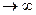 ) более высокого порядка, чем xk для любого k, а log ax – бесконечно большая низшего порядка, чем любая степень хk .
) более высокого порядка, чем xk для любого k, а log ax – бесконечно большая низшего порядка, чем любая степень хk . при | x - x0 | < δ. Для этого достаточно выбрать в качестве ε 1/ M. Тогда при | x - x0 | < δ | α(x)|< 1/ M, следовательно,
при | x - x0 | < δ. Для этого достаточно выбрать в качестве ε 1/ M. Тогда при | x - x0 | < δ | α(x)|< 1/ M, следовательно,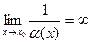 , то есть 1/ α(х ) – бесконечно большая при х→х0.
, то есть 1/ α(х ) – бесконечно большая при х→х0. 
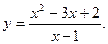
 , то есть х = 1 – устранимая особенность.
, то есть х = 1 – устранимая особенность. Из определения модуля следует, что у = 1 при x > 0, y = -1 при x < 0, а при х = 0 функция не определена. При этом
Из определения модуля следует, что у = 1 при x > 0, y = -1 при x < 0, а при х = 0 функция не определена. При этом  . Следовательно, х = 0 –точка разрыва 1-го рода.
. Следовательно, х = 0 –точка разрыва 1-го рода.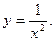 Функция не определена при х = 0, и
Функция не определена при х = 0, и  . Поэтому х = 0 – точка разрыва 2-го рода.
. Поэтому х = 0 – точка разрыва 2-го рода.
 то есть правосторонний предел не является конечным. Значит, х = 0 – точка разрыва 2-го рода.
то есть правосторонний предел не является конечным. Значит, х = 0 – точка разрыва 2-го рода.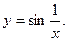 Функция не определена при х = 0 и не имеет предела при х →0. Следовательно, х = 0 – точка разрыва 2-го рода.
Функция не определена при х = 0 и не имеет предела при х →0. Следовательно, х = 0 – точка разрыва 2-го рода.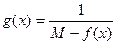 . По выдвинутому предположению знаменатель дроби в 0 не обращается, следовательно, g(x) непрерывна на [ ab ] и поэтому ограничена (т.16.1):
. По выдвинутому предположению знаменатель дроби в 0 не обращается, следовательно, g(x) непрерывна на [ ab ] и поэтому ограничена (т.16.1): Но из этого следует, что
Но из этого следует, что 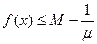 , то есть число
, то есть число  , меньшее М, оказывается верхней гранью f(x ), что противоречит выбору М. Значит, на [ ab ] найдется значение х 0 такое, что f(x0)=M. Аналогичным образом можно доказать и то, что f(x ) достигает на [ ab ] своей нижней грани.
, меньшее М, оказывается верхней гранью f(x ), что противоречит выбору М. Значит, на [ ab ] найдется значение х 0 такое, что f(x0)=M. Аналогичным образом можно доказать и то, что f(x ) достигает на [ ab ] своей нижней грани.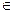 [ ab ]: f(x0)=C .
[ ab ]: f(x0)=C .
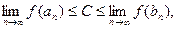 то есть f(x0) ≤ C ≤ f(x0 ), или С = f(x0 ).
то есть f(x0) ≤ C ≤ f(x0 ), или С = f(x0 ). , то
, то 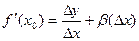 , где β(Δх) – бесконечно малая при Δ х →0. Тогда
, где β(Δх) – бесконечно малая при Δ х →0. Тогда  . Следовательно, функция y = f(x ) дифференцируема при х = х0, причем А = f`(x0 ).
. Следовательно, функция y = f(x ) дифференцируема при х = х0, причем А = f`(x0 ). . Таким образом, f(x ) имеет производную в точке х0, равную А.
. Таким образом, f(x ) имеет производную в точке х0, равную А. , а производную – в виде
, а производную – в виде  .
. , что и означает непрерывность f(x) при х = х0 .
, что и означает непрерывность f(x) при х = х0 . . Пусть
. Пусть  Тогда
Тогда
 (18.1)
(18.1)
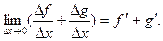
 где k =const. (18.2)
где k =const. (18.2)
 (18.3)
(18.3)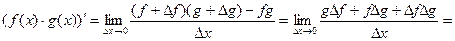
 так как
так как  в силу непрерывности g(x).
в силу непрерывности g(x). 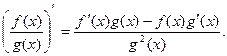 (18.4)
(18.4)
 то по третьему определению предела можно представить
то по третьему определению предела можно представить где
где  при
при  Тогда
Тогда  Разделив обе части равенства на Δ х, получим:
Разделив обе части равенства на Δ х, получим: . Переходя к пределу при Δ х →0, получаем:
. Переходя к пределу при Δ х →0, получаем:  так как
так как 
 Так как φ(у ) непрерывна, Δ х →0 при Δ у →0, и при переходе к пределу при Δ у →0 получаем:
Так как φ(у ) непрерывна, Δ х →0 при Δ у →0, и при переходе к пределу при Δ у →0 получаем:  .
. следовательно,
следовательно,  Но
Но  поэтому
поэтому  Таким образом, форма дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. Это свойство называется свойством неизменности, или инвариантности, дифференциала.
Таким образом, форма дифференциала не зависит от того, является аргумент функции независимой переменной или функцией другого аргумента. Это свойство называется свойством неизменности, или инвариантности, дифференциала.


 .
. и максимумы при
и максимумы при 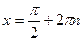 .
. а если x > x0,
а если x > x0, 


 у у у
у у у







 Доказательство. Докажем первое утверждение теоремы. Пусть f ′′(x) < 0 на (ab).
Доказательство. Докажем первое утверждение теоремы. Пусть f ′′(x) < 0 на (ab).

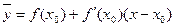 .
.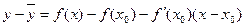 . Применив теорему Лагранжа, получим:
. Применив теорему Лагранжа, получим: 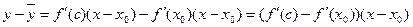 , где с лежит между х и х0. Применим к первому множителю правой части полученного равенства еще раз теорему Лагранжа:
, где с лежит между х и х0. Применим к первому множителю правой части полученного равенства еще раз теорему Лагранжа: 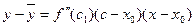 (23.1)
(23.1)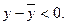 Если же x < x0, то x < c < c1 < x0, поэтому c – x0 < 0, x – x0 < 0, f ′′(c1) < 0. Но при этом по-прежнему
Если же x < x0, то x < c < c1 < x0, поэтому c – x0 < 0, x – x0 < 0, f ′′(c1) < 0. Но при этом по-прежнему  , по формуле Тейлора получаем:
, по формуле Тейлора получаем: 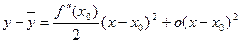 . Если бы
. Если бы 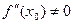 , разность
, разность 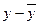 сохраняла бы постоянный знак в некоторой окрестности точки х0, в то время как в точке перегиба эта разность должна менять знак. Следовательно, f ′′(x0) = 0.
сохраняла бы постоянный знак в некоторой окрестности точки х0, в то время как в точке перегиба эта разность должна менять знак. Следовательно, f ′′(x0) = 0. конечен, т.е.
конечен, т.е. 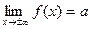 .
.


