
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение касательной к графику функции.
Составим уравнение касательной к графику функции y = f(x) при х = х0. Эта прямая должна проходить через точку с координатами ( х0,у0 ), лежащую на графике функции, где у0 = f(x0), и иметь угловой коэффициент, равный производной f(x ) при х = х0. Воспользовавшись уравнением (7.9), получим: у = f`(x0)х + b, причем у0 = f`(x0)x0 + b, то есть b = y0 - f`(x0)x0. Тогда уравнение касательной можно записать в виде:
Дифференцируемость функции. Определение 17.2. Если приращение функции y = f(x) при х = х0 можно представить в виде
где A = const, то y = f(x ) называется дифференцируемой при х = х0, а АΔх называется главной линейной частью приращения или дифференциалом функции. Обозначение: dy = АΔх. Замечание. Так как при у = х получаем dx = 1·Δx, можно обозначать Δх = dx . Теорема 17.1. Функция дифференцируема в некоторой точке в том и только в том случае, если она имеет в этой точке производную. Доказательство. 1) Если для y=f(x) существует 2) Пусть y=f(x ) дифференцируема при х=х0, то есть ее приращение имеет вид (17.2). Тогда Следствие. Дифференциал функции можно представить в виде Теорема 17.2. Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке. Доказательство. Из формулы (17.2) следует, что Замечание. Обратное утверждение неверно, то есть из непрерывности функции не следует ее дифференцируемость. Например, y = |x | непрерывна при х = 0, но не дифференцируема в этой точке. Геометрический смысл дифференциала
В касательную к нему при х=х0. Тогда при прира- щении аргумента Δ х приращение функции Δ у С равно длине отрезка BD, а приращение ордина- ты касательной А D отрезка CD. Следовательно, дифференциал функции равен приращению ординаты Δ х касательной. х0 х Линеаризация функции. Так как истинное значение приращения функции отличается от ее дифференциала на бесконечно малую более высокого порядка, чем Δ х, при приближенных вычислениях можно заменять Δ у на dy, то есть считать, что f(x0 + Δx) ≈ f(x0) + dy = f(x0) + f`(x0)(x -x0 ). При этом функция f(x ) для значений х, близких к х0, приближенно заменяется линейной функцией. Эта операция называется линеаризацией функции.
Пример. Найдем приближенное значение
Лекция 18. Свойства производной (правила дифференцирования). Производная сложной и обратной функций. Инвариантность формы дифференциала. Таблица производных, логарифмическое дифференцирование. Дифференцирование функций, заданных параметрически.
Правила дифференцирования. Пусть при рассматриваемых значениях х существуют производные функций f(x ) и g(x ), то есть эти функции являются дифференцируемыми при данных значениях аргумента. Сформулируем и докажем некоторые свойства производных. 1. Доказательство.
2. Доказательство. 3. Доказательство.
4. Если g(x)≠ 0, то Доказательство.
|
|||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 242; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.81.240 (0.008 с.) |
 или
или 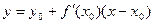 (17.1)
(17.1)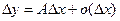 , (17.2)
, (17.2) , то
, то 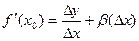 , где β(Δх) – бесконечно малая при Δ х →0. Тогда
, где β(Δх) – бесконечно малая при Δ х →0. Тогда  . Следовательно, функция y = f(x ) дифференцируема при х = х0, причем А = f`(x0 ).
. Следовательно, функция y = f(x ) дифференцируема при х = х0, причем А = f`(x0 ). . Таким образом, f(x ) имеет производную в точке х0, равную А.
. Таким образом, f(x ) имеет производную в точке х0, равную А. , а производную – в виде
, а производную – в виде  .
. , что и означает непрерывность f(x) при х = х0 .
, что и означает непрерывность f(x) при х = х0 .







 у Рассмотрим график функции y=f(x ) и проведем
у Рассмотрим график функции y=f(x ) и проведем равно длине
равно длине . Пусть
. Пусть  Тогда
Тогда
 (18.1)
(18.1)
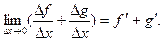
 где k =const. (18.2)
где k =const. (18.2)
 (18.3)
(18.3)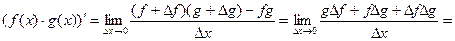
 так как
так как  в силу непрерывности g(x).
в силу непрерывности g(x). 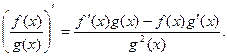 (18.4)
(18.4)



