
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оптическая пирометрия. Температуры. Принцип измерения температуры.Содержание книги
Поиск на нашем сайте
Оптическая пирометрия. Оптической пирометрией называется совокупность методов измерения температуры тел, основанных на законах теплового излучения. Приборы, применяемые для этого, называются пирометрами. Эти методы очень удобны для измерения температур различных объектов, где сложно или вообще невозможно применить традиционные контактные датчики. Это относится в первую очередь к измерению высоких температур. В оптической пирометрии различают следующие температуры тела: радиационную, цветовую, яркостную. Радиационная температура. Радиационная температура Тр тела - это температура абсолютно чёрного тела, при которой его энергетическая светимость R равна энергетической светимости Rm данного тела в широком диапазоне длин волн. Если же измерить мощность, излучаемую некоторым телом с единицы поверхности в достаточно широком интервале волн и ее величину сопоставить с энергетической светимостью абсолютно черного тела, то можно, используя формулу (11), вычислить температуру этого тела, как
Определенная таким способом температура Tp будет достаточно точно соответствовать истинной температуре T при выполнении двух условий: -оптическая система и детектор излучения должны иметь одинаковую чувствительность в широком диапазоне длин волн, соответствующем основной излучаемой мощности поверхности тела. -коэффициент монохроматического поглощения поверхности тела должен быть близок к единице. Для серого тела закон Стефана-Больцмана может быть записан в виде Rm(T) = αT σT 4; где αT < 1. Подставляя данное выражение в формулу (17), получим
Из (18) следует, что для серого тела радиационная температура оказывается всегда ниже истинной (Tp < T).
3.2. Цветовая температура. Спектральная плотность энергетической светимости серых тел (или тел близких к ним по свойствам) с точностью до постоянного коэффициента (коэффициента монохроматического поглощения) пропорциональна спектральной плотности энергетической светимости абсолютно черного тела. Следовательно, распределение энергии в спектре серого тела такое же, как и в спектре абсолютно черного тела при той же температуре. Для определения температуры серого тела достаточно измерить мощность I(λ,Т), излучаемую единицей поверхности тела в достаточно узком спектральном интервале (пропорциональную r(λ,Т)), для двух различных волн. Отношение I(λ,Т) для двух длин волн равно отношению зависимостей f(λ,Т) для этих волн, вид которых дается формулой (5):
Из данного равенства можно математическим путем получить температуру Т. Полученная таким образом температура называется цветовой. Цветовая температура тела, определенная по формуле (19), будет соответствовать истинной, если коэффициент монохроматического поглощения не сильно зависит от длины волны. В противном случае понятие цветовой температуры теряет смысл. Цветовая температура серого тела совпадает с истинной температурой и может быть найдена также из закона смещения Вина. Таким образом, цветовая температура Тц тела - это температура абсолютно чёрного тела, при которой относительные распределения спектральной плотности энергетической светимости абсолютно чёрного тела и рассматриваемого тела максимально близки в видимой области спектра. Обычно для определения цветовой температуры выбирают длины волн λ1=655 нм (красный цвет), λ2= 470 нм (зелено-голубой цвет).
3.3. Яркостная температура.
Яркостная температура Тя тела – это температура абсолютно чёрного тела, при которой его спектральная плотность энергетической светимости f(λ,T), для какой либо определённой длины волны, равна спектральной плотности, энергетической светимости r(λ,Т) данного тела для той же длины волны. Так как для нечерного тела спектральная плотность энергетической светимости при определенной температуре будет всегда ниже чем у абсолютно черного тела, то истинная температура тела будет всегда выше яркостной. В качестве яркостного пирометра широко используется пирометр с исчезающей нитью. Принцип определения температуры основан на визуальном сравнении яркости раскаленной нити лампы пирометра с яркостью изображения исследуемого объекта. Равенство яркостей, наблюдаемое через монохроматический светофильтр (обычно измерения проводят на длине волны λ =660 нм), определяется по исчезновению изображения нити пирометрической лампы на фоне изображения раскаленного объекта. Накал нити лампы пирометра регулируется реостатом, а температура нити определяется по градуировочному графику, или таблице. Если температура нити высока, то для ослабления потока излучения применяется также и нейтральный светофильтр. Пусть мы в результате измерений получили равенство яркостей нити пирометра и исследуемого объекта и по графику определили температуру нити пирометра Т1. Тогда, на основании формулы (3) можно записать: f (λ,T1) α1 (λ,T1) = f (λ,T2) α2 (λ, T2 ) (20)
где α1 (λ,T1) и α2 (λ,T2) коэффициенты монохроматического поглощения материала нити пирометра и исследуемого объекта соответственно. T1 и T2 – температуры нити пирометра и объекта. Как видно из (20), равенство температур объекта и нити пирометра будут наблюдаться только тогда, когда будут, равны их коэффициенты монохроматического поглощения в наблюдаемой области спектра α1 (λ,T1) = α2 (λ,T2). Если α1 (λ,T1) > α2 (λ,T2), мы получим заниженное значение температуры объекта, при обратном соотношении - завышенное значение температуры.
4. Определение постоянной Стефана-Больцмана с помощью оптического пирометра Для реальных (не черных, в том числе и серых) тел на основании закона Стефана-Больцмана можно определить мощность излучения во всем интервале длин волн W: W = α(Т) S σТ 4 (21) где S – площадь поверхности нагретого тела, α(Т) –коэффициент черноты реального тела. Он равен отношению энергетической светимости данного реального тела к энергетической светимости абсолютно черного тела при той же температуре. Данный коэффициент представляет интегральный (по всем длинам волн) коэффициент поглощения реального тела. Для серого тела этот коэффициент представляет собой коэффициент монохроматического поглощения α Т, не зависящий от длины волны (введен ранее в 2.2). В качестве тела-источника теплового излучения можно взять вольфрамовую спираль вакуумной лампы накаливания. Подводимая энергия электрического тока в такой лампе расходуется в основном на тепловое излучение. Доля рассеиваемой мощности лампы за счет теплопроводности составляет небольшую величину и ею можно пренебречь в общем балансе энергии. Таким образом, с одной стороны, мы можем определить мощность излучения из закона Джоуля-Ленца, с другой, определить температуру нити лампы с помощью оптического пирометра. При этом температура, определенная с помощью пирометра, будет истинной, поскольку нити лампы пирометра и исследуемой лампы изготовлены из одного материала - вольфрама. Поэтому можно записать: W= Iл Uл = α(Т) S б Т4 (22)
где Iл, Uл - ток и напряжение питания лампы. Зная длину и диаметр нити накала, а также коэффициент черноты α(Т) вольфрама в видимой области спектра, легко вычислить постоянную Стефана-Больцмана:
Площадь нити исследуемой лампы накаливания S =0.317·10 -3м2. Коэффициент α(Т) = 0.25.
32Элементарная теория эффекта К о мптона. Квантовое (корпускулярное) свойство света проявляется в таких явлениях, как внешний и внутренний фотоэффект, тепловое излучение, эффект Комптона. Эффект Комптона состоит в увеличении длины волны света, рассеянного свободным или слабосвязанным электронами вещества, причём излучение λ зависит от угла рассеивания. Этот эффект для коротких λ. По классическим представлениям, электрон в поле падающей волны должен колебаться с частотой этой волны и испускать во все стороны световые волны той же частоты. Это наблюдается только для длинных λ. Эффект Комптона объясняется только с использованием взаимодействия фотона и электронов. Пусть рассеивание происходит так: падающий фотон мгновенно поглощается электроном, затем электрон излучает рассеивание фотонов.
ЗСЭ для такого процесса рассеивания имеет вид
По PCB при рассеивании для системы электрон – фотон.
Отсюда - формула Комптона. Т.к.
Давление света. Фотон обладает импульсом. При падении его на поверхность тела он может передать импульс этому телу => оказать давление на эту поверхность. Выведем формулу для давления D света на поверхность тела. Пусть на единицу площади поверхности за единицу времени падает N фотонов. Если фотон поглощается поверхность, то он передаёт ей свой импульс
Выделяемый, с помощью узкого отверстия в контейнере пучок альфа-частиц, испускаемых радиоактивным источником И, падал на тонкую металлическую фольгу Ф. При прохождении через фольгу альфа-частицы отклонялись от первоначального направления движения на различные углы b. Рассеянные альфа-частицы ударялись об экран Э, покрытый сернистым цинком, и вызываемые ими сцинтилляции (вспышки света) наблюдались в микроскоп М. Микроскоп и экран можно было вращать вокруг оси, проходящей через центр фольги, и устанавливать таким образом под любым углом b. Весь прибор помещался в вакуумную камеру, чтобы устранить рассеяние альфа-частиц за счет столкновения с молекулами воздуха. Основная часть альфа частиц отклоняется от первоначального направления на небольшие углы, но угол рассеяния небольшого количества альфа-частиц оказывается значительно большим и может достигать 180о. Резерфорд пришел к выводу, что отклонение альфа-частиц от первоначального направления возможно только, когда внутри атома имеется электрическое поле, которое создается зарядом, связанным с большой массой. Малая доля частиц, рассеиваемых на большие углы, указывает на то, что положительный заряд и связанная с ним масса сосредоточены в очень малом объеме и вероятность прямого попадания мала. Основываясь на этом выводе, Резерфорд предложил ядерную модель атома. Согласно Резерфорду атом представляет собой систему зарядов, в центре которой расположено тяжелое положительно заряженное ядро, имеющее размеры до 10-12 см, а вокруг ядра вращаются отрицательно заряженные электроны, суммарный заряд которых равен по модулю заряду ядра. Почти вся масса атома сосредоточена в ядре. Но электрон, двигаясь по искривленной траектории должен иметь центростремительное ускорение. По законам классической электродинамики заряд, движущийся с ускорением, должен непрерывно излучать электромагнитные волны. Процесс излучения сопровождается потерей энергии, так что электрон должен постепенно опускаться, двигаясь по спирали и, в конечном счете, упасть на ядро. При этом, непрерывно изменяя радиус своей орбиты, он должен излучать сплошной спектр, но в опытах с разреженными газами установлено, что спектры атомов являются линейчатыми. Противоречие.
Выход из противоречия предложил Нильс Бор, который следующие постулаты: 1) Из бесконечного множества электронных орбит, возможных для электрона в атоме с точки зрения классической механики, на самом деле реализуются лишь некоторые, называемые стационарными. Находясь на стационарной орбите электрон не излучает энергию (э/м волны) хотя и движется с ускорением. Для стационарной орбиты момент импульса электрона должен быть целым кратным от постоянной величины
где me – масса электрона, v –скорость электрона, r – радиус электронной орбиты, n – целое число, которое может принимать значения 1, 2, 3, 4…и называется главным квантовым числом. 2) Излучение испускается или поглощается атомом в виде светового кванта энергии
Такое же соотношение справедливо и для случая поглощения. Соотношение (2) называется правилом частот Бора.
В основу модели атома водорода Бор положил планетарную модель атома Резерфорда и постулаты. Из первого постулата Бора следует, что возможными являются лишь такие орбиты движения электрона вокруг ядра, для которых момент импульса электрона равен целому кратному от постоянной Дирака
исключая скорость из уравнений (1) и (3), было получено выражение для радиусов допустимых орбит:
(4)
здесь n – главное квантовое число (n = 1,2,3…
(5) Внутренняя энергия атома равна сумме кинетической энергии электрона и потенциальной энергии взаимодействия электрона с ядром (ядро, ввиду его большой массы, в первом приближении считается неподвижным).
так как (смотри формулу (3))
Подставив в (6) выражение rn из (4), найдём разрешённые значения внутренней энергии атома:
(8)
где n = 1, 2, 3, 4… При переходе атома водорода из состояния n1 в состояние n2 излучается фотон.
Обратная длина волны испускаемого света может быть рассчитана по формуле: (11)
|
|||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 276; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.207.196 (0.01 с.) |

 (17)
(17)
 (18)
(18) (19)
(19)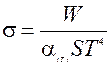 (23)
(23)

 - энергетическая концентрация фотона,
- энергетическая концентрация фотона,  - энергия покоя фотона,
- энергия покоя фотона,  - энергетическая рассеивание фотона,
- энергетическая рассеивание фотона,  - энергия электрона после рассеивания. При рассеивании электрон получит большую скорость. Воспользуемся теорией относительности:
- энергия электрона после рассеивания. При рассеивании электрон получит большую скорость. Воспользуемся теорией относительности: .
.
 – импульс фотона.
– импульс фотона.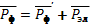


 , то
, то  , где
, где  - Комптонская длина волны. => для нерассеиванного фотона
- Комптонская длина волны. => для нерассеиванного фотона 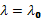 , для рассеиванного -
, для рассеиванного -  .
. . Если фотон отражается от поверхности, то она предаёт.Если коэффициент отражения света R, то ежесекундно на единице поверхности помещается (1-R)N фотонов и отражается RN фотонов. => поверхность получает импульс
. Если фотон отражается от поверхности, то она предаёт.Если коэффициент отражения света R, то ежесекундно на единице поверхности помещается (1-R)N фотонов и отражается RN фотонов. => поверхность получает импульс  Эта величина является также давлением, оказанным падающим светом на поверхность.
Эта величина является также давлением, оказанным падающим светом на поверхность.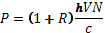 , где
, где  - плотность потока энергии на поверхности или энергетическая освещённость.
- плотность потока энергии на поверхности или энергетическая освещённость. 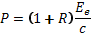 . Это же уравнение можно получить волновой теорией света из уравнения Максвелла. Отметим, что для абсолютно чёрного тела R=0, а для зеркальной поверхности R=1.
. Это же уравнение можно получить волновой теорией света из уравнения Максвелла. Отметим, что для абсолютно чёрного тела R=0, а для зеркальной поверхности R=1. 34Строение атома. Опыты Резерфорда. Постулаты Бора. Теория атома водорода.
34Строение атома. Опыты Резерфорда. Постулаты Бора. Теория атома водорода. (
( – постоянная Дирака). Т.е. должно выполняться соотношение:
– постоянная Дирака). Т.е. должно выполняться соотношение: (1)
(1) при переходе электрона из одного стационарного (устойчивого) состояния в другое. Величина светового кванта равна разности энергий тех стационарных состояний E n 1 и E n 2 , между которыми совершается квантовый скачок электрона:
при переходе электрона из одного стационарного (устойчивого) состояния в другое. Величина светового кванта равна разности энергий тех стационарных состояний E n 1 и E n 2 , между которыми совершается квантовый скачок электрона: (2)
(2) (см. (1)). Далее Бор применил законы классической физики. В соответствии со вторым законом Ньютона, для электрона, вращающегося вокруг ядра, кулоновская сила играет роль центростремительной силы и должно выполняться соотношение:
(см. (1)). Далее Бор применил законы классической физики. В соответствии со вторым законом Ньютона, для электрона, вращающегося вокруг ядра, кулоновская сила играет роль центростремительной силы и должно выполняться соотношение: (3)
(3)
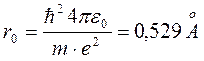 Радиус первой орбиты водородного атома называется Боровским радиусом и равен
Радиус первой орбиты водородного атома называется Боровским радиусом и равен (6)
(6)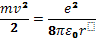 (7)
(7)
 (9)
(9) (10)
(10)


