
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поглощение и рассеяние излучения. Закон Бугера. Рассеяние излучения в мутных средах.Содержание книги
Поиск на нашем сайте
Под поглощ света понимают превращ энергии свет волны из электромагн формы во внутр энергию (тепловую) среды, в которой проходит волна. Поглощ света описывается законом Бугера:
k обратнопропорц толщине поглощ слоя, при прохожд которого Если слой не только поглощ свет, но и отражает его, то С отражением света может происходить его рассеивание, под которым понимают перераспределение энергии св волны по разным направления из-за дифракции на мелких неоднор телах среды, называемые мутными (дым, туман). приd<<λ и приd=λ. Доп особенность света явл его поляриз при рассеивании на 900 в направл ⊥ падающему лучу. В естеств. свете колебания E можно разложить на 2 взаимно⊥ направления, которые вызывают вынужденное колебание электронов в в-ве. Электроны, связанные с атомом представл собой диполи, излуча-ие электромагн волны в направл ⊥ своей оси. Тепловое излучение. Энергетическая светимость. Спектральная плотность светимости. Абсолютно чёрное тело. Закон Кирхгофа. Закон Стефана-Больцмана. Тепловое излучение тел. Тепловым излучением тел называется электромагнитное излучение, возникающее за счет той части внутренней энергии тела, которая связана с тепловым движением его частиц. Основными характеристиками теплового излучения тел нагретых до температуры T являются: 1. Энергетическая светимость R ( T ) - количество энергии, излучаемой в единицу времени с единицы поверхности тела, во всем интервале длин волн. Зависит от температуры, природы и состояния поверхности излучающего тела. В системе СИ R(T) имеет размерность [Вт/м2]. 2. Спектральная плотность энергетической светимости r(l,Т) = dW/dl - количество энергии, излучаемое единицей поверхности тела, в единицу времени в единичном интервале длин волн (вблизи рассматриваемой длины волны l). Т.е. эта величина численно равна отношению энергии dW, испускаемой с единицы площади в единицу времени в узком интервале длин волн от l до l+dl, к ширине этого интервала. Она зависит от температуры тела, длины волны, а также от природы и состояния поверхности излучающего тела. В системе СИ r(l, T) имеет размерность [Вт/м3]. Энергетическая светимость R(T) связана со спектральной плотностью энергетической светимости r(l, T) следующим образом:
3. Все тела не только излучают, но и поглощают падающие на их поверхность электромагнитные волны. Для определения поглощательной способности тел по отношению к электромагнитным волнам определенной длины волны вводится понятие коэффициента монохроматического поглощения - отношение величины поглощенной поверхностью тела энергии монохроматической волны к величине энергии падающей монохроматической волны:
Коэффициент монохроматического поглощения является безразмерной величиной, зависящей от температуры и длины волны. Он показывает, какая доля энергии падающей монохроматической волны поглощается поверхностью тела. Величина a (l,T) может принимать значения от 0 до 1. Излучение в адиабатически замкнутой системе (не обменивающейся теплотой с внешней средой) называется равновесным. Если создать маленькое отверстие в стенке полости состояние равновесия измениться слабо и выходящее из полости излучение будет соответствовать равновесному излучению. Если в такое отверстие направить луч, то после многократных отражений и поглощения на стенках полости он не сможет выйти обратно наружу. Это значит, что для такого отверстия коэффициент поглощения a (l, T) = 1. Рассмотренная замкнутая полость с небольшим отверстием служит одной из моделей абсолютно черного тела. Абсолютно черным телом называется тело, которое поглощает все падающее на него излучение независимо от направления падающего излучения, его спектрального состава и поляризации (ничего не отражая и не пропуская). Для абсолютно черного тела, спектральная плотность энергетической светимости является некоторой универсальной функцией длины волны и температуры f(l,T) и не зависит от его природы. Все тела в природе частично отражают падающее на их поверхность излучение и поэтому не относятся к абсолютно черным телам. Если коэффициент монохроматического поглощения тела одинаков для всех длин волн и меньше единицы (a(l, T) = aТ = const<1), то такое тело называется серым. Коэффициент монохроматического поглощения серого тела зависит только от температуры тела, его природы и состояния его поверхности. Кирхгофом было показано, что для всех тел, независимо от их природы, отношение спектральной плотности энергетической светимости к коэффициенту монохроматического поглощения является той же универсальной функцией длины волны и температуры f(l,T), что и спектральная плотность энергетической светимости абсолютно черного тела:
Уравнение (3) представляет собой закон Кирхгофа. Закон Кирхгофа можно сформулировать таким образом: для всех тел системы, находящихся в термодинамическом равновесии, отношение спектральной плотности энергетической светимости к коэффициенту монохроматического поглощения не зависит от природы тела, является одинаковой для всех тел функцией, зависящей от длины волны l и температуры Т. Из вышесказанного и формулы (3) ясно, что при данной температуре сильнее излучают те серые тела, которые обладают большим коэффициентом поглощения, а наиболее сильно излучают абсолютно черные тела. Так как для абсолютно черного тела a(l, T)=1, то из формулы (3) следует, что универсальная функция f (l, T) представляет собой спектральную плотность энергетической светимости абсолютно черного тела Закон Стефана – Больцмана Больцман из термодинамических представлений получили зависимость энергетической светимости абсолютно черного тела от температуры:
где постоянная σ =5.67 10-8 Вт/(м2 К4) - постоянная Стефана-Больцмана. Из выражения (11) можно сформулировать закон Стефана-Больцмана: Энергетическая светимость абсолютно чёрного тела пропорциональна четвёртой степени его термодинамической температуры. Формулу (11) можно получить, используя формулу Планка (5). Для этого необходимо в формулу (1) подставить выражение (5) и провести интегрирование по всем длинам волн (от нуля до бесконечности):
Введем новую переменную:
Подставив (13) в (12), получим:
Если учесть, что значение несобственного интеграла в (14) равно π 4/15, получим:
Из сравнения (11) с (15) следует, что постоянная Стефана-Больцмана равна:
Формула Планка. Закон Вина. Формула Планка.
Выражение для спектральной плотности энергетической светимости абсолютно черного тела было получено впервые немецким физиком М. Планком. Согласно квантовой гипотезе Планка испускание энергии электромагнитных волн атомами вещества может происходить только отдельными "порциями" - квантами. При этом энергия кванта света пропорциональна его частоте n:
Постоянная h была названа постоянной Планка, c -скорость света в вакууме. На основании этой гипотезы, используя статистические методы, он получил следующую формулу для универсальной функции f, в которую входит энергия кванта h n:
где k -постоянная Больцмана. Формулу для универсальной функции, зависящей от длины волны l (а не от частоты n) можно вывести используя определение спектральной плотности энергетической светимости
Знак “минус” здесь не играет существенной роли и отражает тот факт, что d n dl имеют разные знаки (т.е. если l увеличивается, n уменьшается) Следовательно,
Рис.1 Зависимость спектральной плотности энергетической светимости абсолютно черного тела от длины волны На рис.1 представлены графики f(l, T) для различных температур. Формула (5*) хорошо согласуется с экспериментальными данными во всем интервале наблюдаемых длин волн и температур и называется формулой Планка. Основные законы излучения абсолютно черного тела можно получить из формулы Планка. Однако многие из них получены на основе экспериментальных данных, а также представлений классической физики еще до открытия Планком своей формулы. Поэтому эти закономерности носят имя ученых, открывших их, и формулируются в виде законов.
Закон смещения Вина.
Из рис.1 видно, что максимум спектральной плотности энергетической светимости с ростом температуры смещается в сторону более коротких волн. Чтобы найти закон смещения данного максимума, необходимо продифференцировать выражение (5) по l и приравнять производную к нулю. Из полученного уравнения можно найти длину волны соответствующую максимуму спектральной плотности энергетической светимости абсолютно черного тела как функцию температуры:
где b - постоянная Вина, lmax - длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости
Закон Вина можно сформулировать следующим образом: Длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости абсолютно черного тела, обратно пропорциональна его температуре.
|
|||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 393; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.22.204 (0.011 с.) |

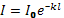 , где l- толщина погл слоя, k-коэф.
, где l- толщина погл слоя, k-коэф. световой волны ум в
световой волны ум в  раз; зависит от природы и плотности в-ва.
раз; зависит от природы и плотности в-ва. , R-коэф отраж.
, R-коэф отраж. (1) [Вт/м2]
(1) [Вт/м2] (2)
(2)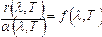 (3)
(3) (11)
(11) (12)
(12) (13)
(13) (14)
(14) (15)
(15) (16)
(16)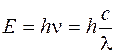
 (4),
(4), .
. (5)
(5)
 (6)
(6) (7)
(7)


