
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Световая волна и её характеристики.Содержание книги
Поиск на нашем сайте
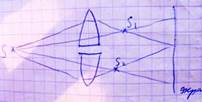
Способы наблюдения интерференции света. Классические интерференционные опыты. Опыт Юнга. Бизеркала Френеля. Бипризмы Френеля. Билинза Бийе. Зеркало Ллойда. В основе интерференционных опытов лежи разделение волны от одного источника на две волны путём отражения или преломления, которые являются когерентными при выполнении: Надо, чтобы две разделённые волны находились внутри области с радиусом. На практике это условие заменяется Оперпюра интерференции – угол между двумя лучами, выходящими из источника и сходящиеся в центре интерференционной картины на экране. Для практической оценки различаемости интерференционных полос используется параметр – видимость.
Мы можем различить интерференционные полосы, если V>0.1, т.е. Опыт Юнга.
Бизеркала в примере. Зеркало разломал на 2 части. Взял источник света.
Бипризма Френеля.
Билинза Френеля.
Зеркало Ллойда.
Во всех эти случаях реализована двулучевая интерференция. Интерференция в тонкой плёнке. Рассмотрим световой луч, который падает из среды с D0 на плоскопараллельную плёнку.
Лучи 1 и 2 являются когерентными. , где
Для упрощения пусть n0=1, тогда ; По закону преломления Максимум при, минимум при Дифракция от прямолинейного края полуплоскости. Спираль Корню. Рассмотрим плоскую световую волну, падающую нормально на бесконечную полуплоскость.
Разобьём волновую поверхность на зоны в виде бесконечно узких полосок так, чтобы границы зон отличались на одинаковую оптическую разность хода ∆. Из рисунка
Для анализа дифракции на полуплоскости используется двойная спираль (Корню).
Пример использования спирали Корню для нахождения результирующей амплитуды светового вектора А в точке наблюдения P на границе.
Зависимость интенсивности вдоль экрана будет иметь вид.
Поляризованный свет. Линейно поляризованный, поляризованный по кругу, эллипсу. Закон Малюса. Естественный свет. Тепловое излучение. Энергетическая светимость. Спектральная плотность светимости. Абсолютно чёрное тело. Закон Кирхгофа. Закон Стефана-Больцмана. Тепловое излучение тел. Тепловым излучением тел называется электромагнитное излучение, возникающее за счет той части внутренней энергии тела, которая связана с тепловым движением его частиц. Основными характеристиками теплового излучения тел нагретых до температуры T являются: 1. Энергетическая светимость R ( T ) - количество энергии, излучаемой в единицу времени с единицы поверхности тела, во всем интервале длин волн. Зависит от температуры, природы и состояния поверхности излучающего тела. В системе СИ R(T) имеет размерность [Вт/м2]. 2. Спектральная плотность энергетической светимости r(l,Т) = dW/dl - количество энергии, излучаемое единицей поверхности тела, в единицу времени в единичном интервале длин волн (вблизи рассматриваемой длины волны l). Т.е. эта величина численно равна отношению энергии dW, испускаемой с единицы площади в единицу времени в узком интервале длин волн от l до l+dl, к ширине этого интервала. Она зависит от температуры тела, длины волны, а также от природы и состояния поверхности излучающего тела. В системе СИ r(l, T) имеет размерность [Вт/м3]. Энергетическая светимость R(T) связана со спектральной плотностью энергетической светимости r(l, T) следующим образом:
3. Все тела не только излучают, но и поглощают падающие на их поверхность электромагнитные волны. Для определения поглощательной способности тел по отношению к электромагнитным волнам определенной длины волны вводится понятие коэффициента монохроматического поглощения - отношение величины поглощенной поверхностью тела энергии монохроматической волны к величине энергии падающей монохроматической волны:
Коэффициент монохроматического поглощения является безразмерной величиной, зависящей от температуры и длины волны. Он показывает, какая доля энергии падающей монохроматической волны поглощается поверхностью тела. Величина a (l,T) может принимать значения от 0 до 1. Излучение в адиабатически замкнутой системе (не обменивающейся теплотой с внешней средой) называется равновесным. Если создать маленькое отверстие в стенке полости состояние равновесия измениться слабо и выходящее из полости излучение будет соответствовать равновесному излучению. Если в такое отверстие направить луч, то после многократных отражений и поглощения на стенках полости он не сможет выйти обратно наружу. Это значит, что для такого отверстия коэффициент поглощения a (l, T) = 1. Рассмотренная замкнутая полость с небольшим отверстием служит одной из моделей абсолютно черного тела. Абсолютно черным телом называется тело, которое поглощает все падающее на него излучение независимо от направления падающего излучения, его спектрального состава и поляризации (ничего не отражая и не пропуская). Для абсолютно черного тела, спектральная плотность энергетической светимости является некоторой универсальной функцией длины волны и температуры f(l,T) и не зависит от его природы. Все тела в природе частично отражают падающее на их поверхность излучение и поэтому не относятся к абсолютно черным телам. Если коэффициент монохроматического поглощения тела одинаков для всех длин волн и меньше единицы (a(l, T) = aТ = const<1), то такое тело называется серым. Коэффициент монохроматического поглощения серого тела зависит только от температуры тела, его природы и состояния его поверхности. Кирхгофом было показано, что для всех тел, независимо от их природы, отношение спектральной плотности энергетической светимости к коэффициенту монохроматического поглощения является той же универсальной функцией длины волны и температуры f(l,T), что и спектральная плотность энергетической светимости абсолютно черного тела:
Уравнение (3) представляет собой закон Кирхгофа. Закон Кирхгофа можно сформулировать таким образом: для всех тел системы, находящихся в термодинамическом равновесии, отношение спектральной плотности энергетической светимости к коэффициенту монохроматического поглощения не зависит от природы тела, является одинаковой для всех тел функцией, зависящей от длины волны l и температуры Т. Из вышесказанного и формулы (3) ясно, что при данной температуре сильнее излучают те серые тела, которые обладают большим коэффициентом поглощения, а наиболее сильно излучают абсолютно черные тела. Так как для абсолютно черного тела a(l, T)=1, то из формулы (3) следует, что универсальная функция f (l, T) представляет собой спектральную плотность энергетической светимости абсолютно черного тела Закон Стефана – Больцмана Больцман из термодинамических представлений получили зависимость энергетической светимости абсолютно черного тела от температуры:
где постоянная σ =5.67 10-8 Вт/(м2 К4) - постоянная Стефана-Больцмана. Из выражения (11) можно сформулировать закон Стефана-Больцмана: Энергетическая светимость абсолютно чёрного тела пропорциональна четвёртой степени его термодинамической температуры. Формулу (11) можно получить, используя формулу Планка (5). Для этого необходимо в формулу (1) подставить выражение (5) и провести интегрирование по всем длинам волн (от нуля до бесконечности):
Введем новую переменную:
Подставив (13) в (12), получим:
Если учесть, что значение несобственного интеграла в (14) равно π 4/15, получим:
Из сравнения (11) с (15) следует, что постоянная Стефана-Больцмана равна:
Формула Планка. Закон Вина. Формула Планка.
Выражение для спектральной плотности энергетической светимости абсолютно черного тела было получено впервые немецким физиком М. Планком. Согласно квантовой гипотезе Планка испускание энергии электромагнитных волн атомами вещества может происходить только отдельными "порциями" - квантами. При этом энергия кванта света пропорциональна его частоте n:
Постоянная h была названа постоянной Планка, c -скорость света в вакууме. На основании этой гипотезы, используя статистические методы, он получил следующую формулу для универсальной функции f, в которую входит энергия кванта h n:
где k -постоянная Больцмана. Формулу для универсальной функции, зависящей от длины волны l (а не от частоты n) можно вывести используя определение спектральной плотности энергетической светимости
Знак “минус” здесь не играет существенной роли и отражает тот факт, что d n dl имеют разные знаки (т.е. если l увеличивается, n уменьшается) Следовательно,
Рис.1 Зависимость спектральной плотности энергетической светимости абсолютно черного тела от длины волны На рис.1 представлены графики f(l, T) для различных температур. Формула (5*) хорошо согласуется с экспериментальными данными во всем интервале наблюдаемых длин волн и температур и называется формулой Планка. Основные законы излучения абсолютно черного тела можно получить из формулы Планка. Однако многие из них получены на основе экспериментальных данных, а также представлений классической физики еще до открытия Планком своей формулы. Поэтому эти закономерности носят имя ученых, открывших их, и формулируются в виде законов.
Закон смещения Вина.
Из рис.1 видно, что максимум спектральной плотности энергетической светимости с ростом температуры смещается в сторону более коротких волн. Чтобы найти закон смещения данного максимума, необходимо продифференцировать выражение (5) по l и приравнять производную к нулю. Из полученного уравнения можно найти длину волны соответствующую максимуму спектральной плотности энергетической светимости абсолютно черного тела как функцию температуры:
где b - постоянная Вина, lmax - длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости
Закон Вина можно сформулировать следующим образом: Длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости абсолютно черного тела, обратно пропорциональна его температуре.
Оптическая пирометрия. Радиационная температура. Радиационная температура Тр тела - это температура абсолютно чёрного тела, при которой его энергетическая светимость R равна энергетической светимости Rm данного тела в широком диапазоне длин волн. Если же измерить мощность, излучаемую некоторым телом с единицы поверхности в достаточно широком интервале волн и ее величину сопоставить с энергетической светимостью абсолютно черного тела, то можно, используя формулу (11), вычислить температуру этого тела, как
Определенная таким способом температура Tp будет достаточно точно соответствовать истинной температуре T при выполнении двух условий: -оптическая система и детектор излучения должны иметь одинаковую чувствительность в широком диапазоне длин волн, соответствующем основной излучаемой мощности поверхности тела. -коэффициент монохроматического поглощения поверхности тела должен быть близок к единице. Для серого тела закон Стефана-Больцмана может быть записан в виде Rm(T) = αT σT 4; где αT < 1. Подставляя данное выражение в формулу (17), получим
Из (18) следует, что для серого тела радиационная температура оказывается всегда ниже истинной (Tp < T).
3.2. Цветовая температура. Спектральная плотность энергетической светимости серых тел (или тел близких к ним по свойствам) с точностью до постоянного коэффициента (коэффициента монохроматического поглощения) пропорциональна спектральной плотности энергетической светимости абсолютно черного тела. Следовательно, распределение энергии в спектре серого тела такое же, как и в спектре абсолютно черного тела при той же температуре. Для определения температуры серого тела достаточно измерить мощность I(λ,Т), излучаемую единицей поверхности тела в достаточно узком спектральном интервале (пропорциональную r(λ,Т)), для двух различных волн. Отношение I(λ,Т) для двух длин волн равно отношению зависимостей f(λ,Т) для этих волн, вид которых дается формулой (5):
Из данного равенства можно математическим путем получить температуру Т. Полученная таким образом температура называется цветовой. Цветовая температура тела, определенная по формуле (19), будет соответствовать истинной, если коэффициент монохроматического поглощения не сильно зависит от длины волны. В противном случае понятие цветовой температуры теряет смысл. Цветовая температура серого тела совпадает с истинной температурой и может быть найдена также из закона смещения Вина. Таким образом, цветовая температура Тц тела - это температура абсолютно чёрного тела, при которой относительные распределения спектральной плотности энергетической светимости абсолютно чёрного тела и рассматриваемого тела максимально близки в видимой области спектра. Обычно для определения цветовой температуры выбирают длины волн λ1=655 нм (красный цвет), λ2= 470 нм (зелено-голубой цвет).
3.3. Яркостная температура.
Яркостная температура Тя тела – это температура абсолютно чёрного тела, при которой его спектральная плотность энергетической светимости f(λ,T), для какой либо определённой длины волны, равна спектральной плотности, энергетической светимости r(λ,Т) данного тела для той же длины волны. Так как для нечерного тела спектральная плотность энергетической светимости при определенной температуре будет всегда ниже чем у абсолютно черного тела, то истинная температура тела будет всегда выше яркостной. В качестве яркостного пирометра широко используется пирометр с исчезающей нитью. Принцип определения температуры основан на визуальном сравнении яркости раскаленной нити лампы пирометра с яркостью изображения исследуемого объекта. Равенство яркостей, наблюдаемое через монохроматический светофильтр (обычно измерения проводят на длине волны λ =660 нм), определяется по исчезновению изображения нити пирометрической лампы на фоне изображения раскаленного объекта. Накал нити лампы пирометра регулируется реостатом, а температура нити определяется по градуировочному графику, или таблице. Если температура нити высока, то для ослабления потока излучения применяется также и нейтральный светофильтр. Пусть мы в результате измерений получили равенство яркостей нити пирометра и исследуемого объекта и по графику определили температуру нити пирометра Т1. Тогда, на основании формулы (3) можно записать: f (λ,T1) α1 (λ,T1) = f (λ,T2) α2 (λ, T2 ) (20)
где α1 (λ,T1) и α2 (λ,T2) коэффициенты монохроматического поглощения материала нити пирометра и исследуемого объекта соответственно. T1 и T2 – температуры нити пирометра и объекта. Как видно из (20), равенство температур объекта и нити пирометра будут наблюдаться только тогда, когда будут, равны их коэффициенты монохроматического поглощения в наблюдаемой области спектра α1 (λ,T1) = α2 (λ,T2). Если α1 (λ,T1) > α2 (λ,T2), мы получим заниженное значение температуры объекта, при обратном соотношении - завышенное значение температуры.
4. Определение постоянной Стефана-Больцмана с помощью оптического пирометра Для реальных (не черных, в том числе и серых) тел на основании закона Стефана-Больцмана можно определить мощность излучения во всем интервале длин волн W: W = α(Т) S σТ 4 (21) где S – площадь поверхности нагретого тела, α(Т) –коэффициент черноты реального тела. Он равен отношению энергетической светимости данного реального тела к энергетической светимости абсолютно черного тела при той же температуре. Данный коэффициент представляет интегральный (по всем длинам волн) коэффициент поглощения реального тела. Для серого тела этот коэффициент представляет собой коэффициент монохроматического поглощения α Т, не зависящий от длины волны (введен ранее в 2.2). В качестве тела-источника теплового излучения можно взять вольфрамовую спираль вакуумной лампы накаливания. Подводимая энергия электрического тока в такой лампе расходуется в основном на тепловое излучение. Доля рассеиваемой мощности лампы за счет теплопроводности составляет небольшую величину и ею можно пренебречь в общем балансе энергии. Таким образом, с одной стороны, мы можем определить мощность излучения из закона Джоуля-Ленца, с другой, определить температуру нити лампы с помощью оптического пирометра. При этом температура, определенная с помощью пирометра, будет истинной, поскольку нити лампы пирометра и исследуемой лампы изготовлены из одного материала - вольфрама. Поэтому можно записать: W= Iл Uл = α(Т) S б Т4 (22)
где Iл, Uл - ток и напряжение питания лампы. Зная длину и диаметр нити накала, а также коэффициент черноты α(Т) вольфрама в видимой области спектра, легко вычислить постоянную Стефана-Больцмана:
Площадь нити исследуемой лампы накаливания S =0.317·10 -3м2. Коэффициент α(Т) = 0.25.
32Элементарная теория эффекта К о мптона. Квантовое (корпускулярное) свойство света проявляется в таких явлениях, как внешний и внутренний фотоэффект, тепловое излучение, эффект Комптона. Эффект Комптона состоит в увеличении длины волны света, рассеянного свободным или слабосвязанным электронами вещества, причём излучение λ зависит от угла рассеивания. Этот эффект для коротких λ. По классическим представлениям, электрон в поле падающей волны должен колебаться с частотой этой волны и испускать во все стороны световые волны той же частоты. Это наблюдается только для длинных λ. Эффект Комптона объясняется только с использованием взаимодействия фотона и электронов. Пусть рассеивание происходит так: падающий фотон мгновенно поглощается электроном, затем электрон излучает рассеивание фотонов.
ЗСЭ для такого процесса рассеивания имеет вид
По PCB при рассеивании для системы электрон – фотон.
Отсюда - формула Комптона. Т.к.
Давление света. Фотон обладает импульсом. При падении его на поверхность тела он может передать импульс этому телу => оказать давление на эту поверхность. Выведем формулу для давления D света на поверхность тела. Пусть на единицу площади поверхности за единицу времени падает N фотонов. Если фотон поглощается поверхность, то он передаёт ей свой импульс
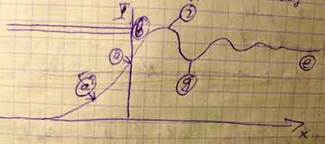
Выделяемый, с помощью узкого отверстия в контейнере пучок альфа-частиц, испускаемых радиоактивным источником И, падал на тонкую металлическую фольгу Ф. При прохождении через фольгу альфа-частицы отклонялись от первоначального направления движения на различные углы b. Рассеянные альфа-частицы ударялись об экран Э, покрытый сернистым цинком, и вызываемые ими сцинтилляции (вспышки света) наблюдались в микроскоп М. Микроскоп и экран можно было вращать вокруг оси, проходящей через центр фольги, и устанавливать таким образом под любым углом b. Весь прибор помещался в вакуумную камеру, чтобы устранить рассеяние альфа-частиц за счет столкновения с молекулами воздуха. Основная часть альфа частиц отклоняется от первоначального направления на небольшие углы, но угол рассеяния небольшого количества альфа-частиц оказывается значительно большим и может достигать 180о. Резерфорд пришел к выводу, что отклонение альфа-частиц от первоначального направления возможно только, когда внутри атома имеется электрическое поле, которое создается зарядом, связанным с большой массой. Малая доля частиц, рассеиваемых на большие углы, указывает на то, что положительный заряд и связанная с ним масса сосредоточены в очень малом объеме и вероятность прямого попадания мала. Основываясь на этом выводе, Резерфорд предложил ядерную модель атома. Согласно Резерфорду атом представляет собой систему зарядов, в центре которой расположено тяжелое положительно заряженное ядро, имеющее размеры до 10-12 см, а вокруг ядра вращаются отрицательно заряженные электроны, суммарный заряд которых равен по модулю заряду ядра. Почти вся масса атома сосредоточена в ядре. Но электрон, двигаясь по искривленной траектории должен иметь центростремительное ускорение. По законам классической электродинамики заряд, движущийся с ускорением, должен непрерывно излучать электромагнитные волны. Процесс излучения сопровождается потерей энергии, так что электрон должен постепенно опускаться, двигаясь по спирали и, в конечном счете, упасть на ядро. При этом, непрерывно изменяя радиус своей орбиты, он должен излучать сплошной спектр, но в опытах с разреженными газами установлено, что спектры атомов являются линейчатыми. Противоречие.
Выход из противоречия предложил Нильс Бор, который следующие постулаты: 1) Из бесконечного множества электронных орбит, возможных для электрона в атоме с точки зрения классической механики, на самом деле реализуются лишь некоторые, называемые стационарными. Находясь на стационарной орбите электрон не излучает энергию (э/м волны) хотя и движется с ускорением. Для стационарной орбиты момент импульса электрона должен быть целым кратным от постоянной величины
где me – масса электрона, v –скорость электрона, r – радиус электронной орбиты, n – целое число, которое может принимать значения 1, 2, 3, 4…и называется главным квантовым числом. 2) Излучение испускается или поглощается атомом в виде светового кванта энергии
Такое же соотношение справедливо и для случая поглощения. Соотношение (2) называется правилом частот Бора.
В основу модели атома водорода Бор положил планетарную модель атома Резерфорда и постулаты. Из первого постулата Бора следует, что возможными являются лишь такие орбиты движения электрона вокруг ядра, для которых момент импульса электрона равен целому кратному от постоянной Дирака
исключая скорость из уравнений (1) и (3), было получено выражение для радиусов допустимых орбит:
(4)
здесь n – главное квантовое число (n = 1,2,3…
(5) Внутренняя энергия атома равна сумме кинетической энергии электрона и потенциальной энергии взаимодействия электрона с ядром (ядро, ввиду его большой массы, в первом приближении считается неподвижным).
так как (смотри формулу (3))
Подставив в (6) выражение rn из (4), найдём разрешённые значения внутренней энергии атома:
(8)
где n = 1, 2, 3, 4… При переходе атома водорода из состояния n1 в состояние n2 излучается фотон.
Обратная длина волны испускаемого света может быть рассчитана по формуле: (11) Световая волна и её характеристики. Оптика – это раздел физики, который изучает распространение света и взаимодействие его с веществом. Свет представляет собой электромагнитное излучение и обладает двойственной природой. В одних явлениях свет ведёт себя как электромагнитная волна, в других – как поток особых частиц фотонов или квантов света. Волновыми свойствами света занимается волновая оптика, квантовой – квантовая. Свет – поток фотонов. С точки зрения волновой оптики световая волна – это процесс колебания электрического и магнитного полей, распространяющихся в пространстве. Оптика занимается световыми волнами, в основном инфракрасного, видимого, ультрафиолетового диапазонов. Как электромагнитная волна свет обладает следующими свойствами (они следуют из уравнения Максвелла): Вектора напряжённости электрического поля E, магнитного поля H и скорость распространения волны V взаимно перпендикулярны и образуют правовинтовую систему.
Вектора E и H колеблются в одной фазе. Для волны выполняется условие: Уравнение световой волны имеет При взаимодействии световой волны с веществом наибольшую роль играет электрическая составляющая волны (магнитная составляющая вне магнитных средах влияет слабее), поэтому E называют световым вектором и его амплитуду Уравнение (1) является решением волнового уравнения, которое имеет вид:
Для немагнитных сред Для плоской волны амплитуда светового вектора уравнения (1) постоянна. Для сферического она уменьшается с расстоянием от источника по закону Перенос энергии световой волны характеризуется вектором Поинтига Он представляет собой плотность потока энергии и направлен по скорости – в сторону его переноса. Вектор S очень быстро изменяется со временем, поэтому любой приёмник излучения, в том числе и глаз, в течение времени наблюдения, гораздо большего, чем период волны, регистрирует усреднённое по времени значение вектора Поинтига, которое называется интенсивностью световой волны. Если усреднить уравнение (4) по времени, то второе слагаемое исчезнет, тогда Интенсивность I – это количество энергии переносимое за единицу времени световой волной через единицу площади. Линию, по которой распространяется энергия волны, называется лучом. Ещё одной характеристикой световой волны является поляризация. Реальный источник состоит из огромного числа атомов, которые излучают, будучи возбуждёнными, в течении t=10-8c, испуская при этом обрывок волны λ=3м. Эти волны имеют различные направления вектора E в пространстве, поэтому в результирующем излучении за время наблюдения встречаются различные направления вектора E, т.е. направление E для реального источника изменяется хаотически по времени, и свет от такого источника называется естественным (неполяризованным). Если же направление колебаний вектора E упорядочены, то такой свет – поляризованный. Различают свет плоско поляризованный, поляризованный по кругу и эллипсу.
Рассмотрим падение плоской световой волны на границе раздела двух прозрачных (не поглощающих) сред с показателями преломления n1 и n2. В этом случае происходит преломление и отражение света. Вывод закона преломления и отражения удобно проводить с помощью принципа Гюйгенса: каждая точка волнового фронта становится источником вторичных сферических волн и новым фронтом волны является огибающая этих вторичных волн. Рассмотрим преломление света.
α – угол падения. BD=L1, AC=L2, AD=L. В первой среде световая волна движется с V1, а во второй с V2. Расстояние L1 и L2 волна проходит за время t => | ||||||||
|
| Поделиться: |

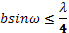 , где -размер источника света;
, где -размер источника света;  – половина угла –оператора интерференции.
– половина угла –оператора интерференции. , где
, где 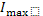 -интенсивность в max.
-интенсивность в max. <0.82
<0.82 




 – длина волны в вакууме.
– длина волны в вакууме. появляется из-за того, что фаза отражённой волны от оптически более плотной волны скачком меняется на Пи.
появляется из-за того, что фаза отражённой волны от оптически более плотной волны скачком меняется на Пи. при n>n0 и при изменении фазы в точке А.
при n>n0 и при изменении фазы в точке А.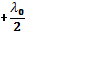 при n<n0 и при изменении фазы в точке В.
при n<n0 и при изменении фазы в точке В.
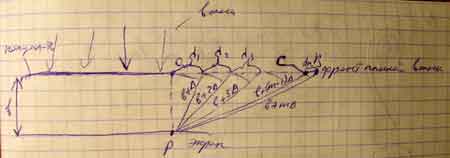
 . => площади зон уменьшаются с ростом m как и
. => площади зон уменьшаются с ростом m как и  . Это значит, что амплитуда вначале изменяется резко, и такому поведению соответствует векторная диаграмма для открытых зон в виде:
. Это значит, что амплитуда вначале изменяется резко, и такому поведению соответствует векторная диаграмма для открытых зон в виде:



 (1) [Вт/м2]
(1) [Вт/м2] (2)
(2)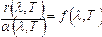 (3)
(3) (11)
(11) (12)
(12) (13)
(13) (14)
(14) (15)
(15) (16)
(16)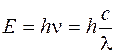
 (4),
(4), .
. (5)
(5)
 (6)
(6) (7)
(7) (17)
(17)
 (18)
(18) (19)
(19)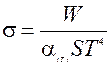 (23)
(23)

 - энергетическая концентрация фотона,
- энергетическая концентрация фотона,  - энергия покоя фотона,
- энергия покоя фотона,  - энергетическая рассеивание фотона,
- энергетическая рассеивание фотона,  - энергия электрона после рассеивания. При рассеивании электрон получит большую скорость. Воспользуемся теорией относительности:
- энергия электрона после рассеивания. При рассеивании электрон получит большую скорость. Воспользуемся теорией относительности: .
.
 – импульс фотона.
– импульс фотона.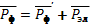


 , то
, то  , где
, где  - Комптонская длина волны. => для нерассеиванного фотона
- Комптонская длина волны. => для нерассеиванного фотона 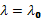 , для рассеиванного -
, для рассеиванного -  .
. . Если фотон отражается от поверхности, то она предаёт.Если коэффициент отражения света R, то ежесекундно на единице поверхности помещается (1-R)N фотонов и отражается RN фотонов. => поверхность получает импульс
. Если фотон отражается от поверхности, то она предаёт.Если коэффициент отражения света R, то ежесекундно на единице поверхности помещается (1-R)N фотонов и отражается RN фотонов. => поверхность получает импульс  Эта величина является также давлением, оказанным падающим светом на поверхность.
Эта величина является также давлением, оказанным падающим светом на поверхность.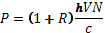 , где
, где  - плотность потока энергии на поверхности или энергетическая освещённость.
- плотность потока энергии на поверхности или энергетическая освещённость. 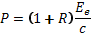 . Это же уравнение можно получить волновой теорией света из уравнения Максвелла. Отметим, что для абсолютно чёрного тела R=0, а для зеркальной поверхности R=1.
. Это же уравнение можно получить волновой теорией света из уравнения Максвелла. Отметим, что для абсолютно чёрного тела R=0, а для зеркальной поверхности R=1. 34Строение атома. Опыты Резерфорда. Постулаты Бора. Теория атома водорода.
34Строение атома. Опыты Резерфорда. Постулаты Бора. Теория атома водорода. (
( – постоянная Дирака). Т.е. должно выполняться соотношение:
– постоянная Дирака). Т.е. должно выполняться соотношение: (1)
(1) при переходе электрона из одного стационарного (устойчивого) состояния в другое. Величина светового кванта равна разности энергий тех стационарных состояний E n 1 и E n 2 , между которыми совершается квантовый скачок электрона:
при переходе электрона из одного стационарного (устойчивого) состояния в другое. Величина светового кванта равна разности энергий тех стационарных состояний E n 1 и E n 2 , между которыми совершается квантовый скачок электрона: (2)
(2) (см. (1)). Далее Бор применил законы классической физики. В соответствии со вторым законом Ньютона, для электрона, вращающегося вокруг ядра, кулоновская сила играет роль центростремительной силы и должно выполняться соотношение:
(см. (1)). Далее Бор применил законы классической физики. В соответствии со вторым законом Ньютона, для электрона, вращающегося вокруг ядра, кулоновская сила играет роль центростремительной силы и должно выполняться соотношение: (3)
(3)
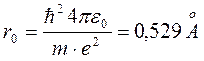 Радиус первой орбиты водородного атома называется Боровским радиусом и равен
Радиус первой орбиты водородного атома называется Боровским радиусом и равен (6)
(6)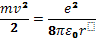 (7)
(7)
 (9)
(9) (10)
(10)

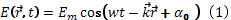 , где
, где  - волновое число,
- волновое число,  - радиус-вектор,
- радиус-вектор,  - начальная фаза.
- начальная фаза. обозначают А.
обозначают А. (2), где
(2), где  - лапласиан; V – фазовая скорость V=c/n (3).
- лапласиан; V – фазовая скорость V=c/n (3). =1 =>
=1 =>  . Из (3) видно, что n=c/v. По виду волновой поверхности различают плоские, сферические, эллиптические и т.д. волны.
. Из (3) видно, что n=c/v. По виду волновой поверхности различают плоские, сферические, эллиптические и т.д. волны.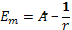 .
. .
. , где. Учитывая (1) и то, что для H оно имеет такой же вид, можно записать, что
, где. Учитывая (1) и то, что для H оно имеет такой же вид, можно записать, что  (4)
(4) (5). Из (5) следует, что I -
(5). Из (5) следует, что I -  (6).
(6). 2Отражение и преломление плоской волны на границе двух диэлектриков. Законы отражения и преломления света.
2Отражение и преломление плоской волны на границе двух диэлектриков. Законы отражения и преломления света. (1). Из ABD и ACD:
(1). Из ABD и ACD:  (2). Отсюда
(2). Отсюда 


