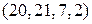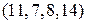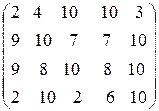Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
IV. Двойственность в линейном программировании.
ДВОЙСТВЕННЫЙ СИМПЛЕКС-МЕТОД
Рассмотрим задачу линейного программирования в общей форме: Z = c1 x1 + c2 x2 +...+ cn xn ® max (1) при ограничениях: y 1³0 a11 x1 + a12 x2 +...+ a1n xn £ b1 y 2³0 a21 x1 + a22 x2 +...+ a2n xn £ b2 ....................................... (2) y k³0 ak1 x1 + ak2 x2 +...+ akn xn £ bk y k+1 ak+1 1 x1 + ak+1 2 x2 +...+ ak+1 n xn = bk+1 ....................................... y m am1 x1 + am2 x2 +...+ amn xn = bm, xj ³ 0, j = 1,..., l; l £ n (3) Каждому i -му ограничению из (2) соответствует переменная y i так называемой двойственной задачи к задаче (1) – (3) (показана слева от соответствующего ограничения). Двойственная задача имеет вид: W = b1 y1 + b2 y2 +...+ bm xm ® min (4) при ограничениях: x1 ³ 0 a11 y1 + a21 y2 +...+ am1 ym ³ c1 x2 ³ 0 a12 y1 + a22 y2 +...+ am2 ym ³ c2 ....................................... (5 ) xl ³ 0 a1l y1 + a2l y2 +...+ aml ym ³ cl xl+1 a1 l+1 y1 + a2 l+1 y2 +...+ a m l+1 ym = cl+1 ....................................... xn a1n y1 + a2n y2 +...+ amn ym = cn, yi ³ 0, i = 1,..., k; k £ n (6) Задачи (1) – (3) и (4) – (6) образуют пару задач, называемую в линейном программировании двойственнойпарой. Сравнивая две задачи, видим, что двойственная задача по отношению к исходной (прямой) содержит те же самые коэффициенты aij, bi, cj и составляется согласно следующим правилам: 1. Целевая функция (1) исходной задачи задается на максимум, а целевая функция (4) двойственной задачи – на минимум. 2. Матрица АТ, составленная из коэффициентов при неизвестных в системе ограничений (5) двойственной задачи получается из матрицы А прямой задачи транспонированием (т.е. заменой строк столбцами):
а11 а12... а1n a11 a21... am1 A = а21 а22... а2n AT = a12 a22... am2 ......................... аm1 аm2... аmn a1n a2n... amn
3. Число переменных в двойственной задаче (4)–(6) равно числу ограничений в системе (2) прямой задачи, а число ограничений в системе (5) двойственной задачи равно числу переменных в прямой задаче. 4. Коэффициентами при неизвестных в целевой функции (4) двойственной задачи являются свободные члены в системе (2) прямой задачи и наоборот. 5. Если переменная xj ³ 0, то j- ое ограничение в системе (5) двойственной задачи является неравенством “ ³ ”. Если же переменная xj может иметь любой знак, то j -ое ограничение в системе (5) представляет собой уравнение. Каждая из задач двойственной пары (1) – (3) и (4) – (6) фактически является самостоятельной задачей линейного программирования и может быть решена независимо одна от другой. Однако при определении симплексным методом оптимального плана одной из задач, тем самым находится решение и другой задачи. Существующие зависимости между решениями прямой и двойственной задач характеризуются сформулированными ниже теоремами двойственности.
Теорема 1. (Основная теорема двойственности). Если одна из пары двойственных задач имеет оптимальный план, то и другая имеет оптимальный план причем значения целевых функций задач при их оптимальных планах совпадают, т.е. Zmax = Wmin. Если же целевая функция одной из задач не ограничена (для исходной (1) – (3) – сверху, для двойственной (4) – (6) – снизу), то другая задача вообще не имеет допустимых решений. Теорема 2. (Вторая теорема двойственности). Для того, чтобы два допустимых решения
Замечание. Соотношения (7) верны только для ограничений в виде неравенств и для неотрицательных переменных.
Двойственный симплекс-метод, как и симплекс-метод, используется при нахождении решения задачи линейного программирования, записанной в канонической форме. Вместе с тем двойственный симплекс-метод можно применять при решении задачи ЛП, свободные члены системы ограничений которой могут быть любыми числами (при решении задачи симплексным методом эти числа предполагались неотрицательными). Опишем алгоритм двойственного симплекс-метода. Рассмотрим задачу линейного программирования в канонической форме.
Пусть матрица ограничений А содержит единичную подматрицу порядка m и первые m переменных
Предположим, что Шаг 1. Составить исходную симплексную таблицу.
Шаг 2. Выяснить, имеется ли хотя бы одно отрицательное число среди элементов столбца b. Если нет, то перейти к шагу 8. Иначе – к шагу 3. Шаг 3. Если отрицательных чисел в столбце b несколько, то выбрать наименьшее. Пусть, для определенности, это число Шаг 4. Среди элементов Шаг 5. Вычислить Шаг 6. С помощью ведущего элемента Шаг 7. Построить новую симплексную таблицу и перейти к шагу 2. Шаг 8. Задача линейного программирования (8) – (10) решена. По последней симплексной таблице выписать оптимальный план и минимальное значение целевой функции задачи (8) – (10). Замечание. Если среди чисел
Пример. Решить задачу линейного программирования: Z = 6x1 + 9x2 + 3x3 ® min
3x1 + x2 – x3 ³ 1 (11) xj ³ 0, j = 1, 2, 3.
Решение. Составим для задачи (11) двойственную: W = 2y1 + y2 ® max
2y1 + y2 £ 9 (12) y1 - y2 £ 3 y1, y2 ³ 0 Для решения задачи (11) двойственным симплекс-методом приведем ее к каноническому виду. Для этого умножим первое и второе ограничения на (-1) и добавим соответственно неотрицательные дополнительные переменные x 4 ³ 0, x5 ³ 0: Z = 6x1 + 9x2 + 3x3 ® min
-3x1 - x2 + x3 + x5 = -1 (13) xj ³ 0, j = 1, 2,..., 5. Базисными переменными здесь являются переменные х 4 и х 5. Поскольку все коэффициенты с j ³ 0, то критерий оптимальности для этого базисного решения выполнен, однако само решение Х = (0, 0, 0, -2, -1) содержит отрицательные переменные, то есть не является допустимым. Естественно попытаться вывести отрицательные (не являющиеся допустимыми) переменные из базиса, сохранив при этом неотрицательность коэффициентов последней строки, так как в этом случае полученное допустимое решение будет являться и оптимальным. Такой подход является содержанием двойственного симплекс-метода. Проиллюстрируем его на примере решения задачи (13). Составим исходную симплекс-таблицу.
Вычисляем Определяем
Элемент b 2 = -3 < 0. Следовательно, разрешающей является вторая строка таблицы. Как и ранее, находим Следовательно второй столбец – разрешающий, переменную х 2 включаем в базис, переменную х 5 исключаем из базиса. Пересчитывая таблицу относительно элемента а 22 = -3, получаем новую таблицу:
Среди элементов столбца “Значение” нет отрицательных чисел. В Z – строке также нет отрицательных чисел. Следовательно, найден оптимальный план: Х * = (0; 1; 0), при этом Z* = Zmin = 9. По последней симплекс-таблице находим решение двойственной задачи (9). Для этого выясняем, какие переменные задачи (10) входили в исходный базис. В первоначальной таблице это – х 4, х 5. В последней симплекс-таблице находим элементы Z – строки, соответствующие этим базисным переменным (с 4 = 4, с 5 = 1) и прибавляем к ним соответствующие коэффициенты исходной целевой функции (с 4 = с 5 = 0). В результате получаем Y * = (4; 1), W * = W max = 9.
КОНТРОЛЬНЫЕ ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ Задание 4. Решить задачу линейного программирования двойственным симплекс-методом. Варианты
1. 2.
V. ТРАНСПОРТНАЯ ЗАДАЧА
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления А 1, А 2,..., А m в n пунктов назначения B1, B 2,..., B n. При этом в качестве критерия оптимальности берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Математическая модель транспортной задачи имеет вид:
Здесь c ij - тарифы перевозки единицы груза из i – го пункта отправления А i в j – ый пункт назначения B j, bj - потребность в грузе в j – ом пункте назначения, ai – запасы груза в i – ом пункте отправления. Наличие линейных уравнений (15) и (16) обеспечивает доставку необходимого количества груза в каждый из пунктов назначения и вывоз всего имеющегося груза из всех пунктов отправления. При этом, ввиду (17), исключаются обратные перевозки. Задача (14) – (17) является частным случаем задачи линейного программирования, однако, в силу своей специфики решается специальным методом. Если выполняется так называемое условие баланса
то такая транспортная задача называется закрытой. Если условие баланса (18) не выполняется, то задача называется открытой.
Теорема 1. Для разрешимости транспортной задачи необходимо и достаточно, чтобы выполнялось условие баланса (5). Если Для решения задачи (14) – (17) применяется метод потенциалов, который по существу, является другой формой симплекс-метода. Опишем алгоритм метода. Исходные данные транспортной задачи запишем в таблице
1. Построение начального опорного плана. Система ограничений (16)-(17) содержит m×n неизвестных и m+ n уравнений, связанных отношением (18). Невырожденный опорный план задачи содержит m + n – 1 положительных перевозок или компонент. Таким образом, если каким-либо способом получен невырожденный опорный план задачи, то в матрице (xij) значений его компонент положительными являются только m + n – 1, а остальные равны нулю. Клетки, в которых находятся отличные от нуля перевозки, называются занятыми, остальные – незанятыми. Занятые клетки соответствуют базисным неизвестным, и для невырожденного опорного плана их количество равно m + n-1. Для построения начального опорного плана применим метод минимальной стоимости. Выбираем клетку с минимальной стоимостью (если их несколько, возьмем любую из них). Пусть, например, Вышеописанную процедуру повторяют для оставшейся транспортной таблицы до тех пор, пока не будут закрыты все строки и столбцы. 2. Построение системы потенциалов. Система потенциалов строится для невырожденного опорного плана и имеет вид:
где Вычисление потенциалов удобно проводить по таблице, положив равным нулю один из потенциалов и затем последовательно находя все остальные потенциалы вычитанием из стоимостей базисных клеток уже известных потенциалов. Потенциалы поставщиков 3. Проверка опорного плана на оптимальность. Для каждой свободной клетки вычисляют оценки
Если
4. Построение цикла и нахождение нового опорного плана. Среди отрицательных оценок выбираем наименьшую. Пусть
В клетке (l, k) нарушено условие оптимальности. Для улучшения опорного плана необходимо в клетку (l, k) отправить некоторое количество груза, превратив ее тем самым в базисную. Эта операция эквивалентна действию по замене базиса в симплекс-методе. Клетку (l, k) отмечают знаком «+» и затем строят цикл, расставляя поочередно знаки «-» и «+» в базисных клетках так, чтобы в строках и столбцах стояло по одному знаку «+» иди «-». Цикл строится единственным образом. Обозначим Замечание. Если условие баланса нарушено, т.е. Пример. Компания контролирует 3 фабрики, производительность которых в неделю (в тыс. изделий) задается вектором Требуется определить оптимальный план перевозок с целью минимизации суммарных затрат на транспортировку. Так как
Таблица 1.
Построим начальный опорный план методом минимального элемента. Первой заполним клетку (1, 3) т. к. тариф этой клетки с 13 = 2 меньше других тарифов (фиктивный столбец заполняется в последнюю очередь). Поставка для клетки (1, 3) будет равна х 13 = min( 30, 25) = 25. Записываем это число в верхний левый угол клетки. Это означает, что с первой фабрики третьему заказчику планируется поставить 25 тыс. ед. груза. При этом требования 3-го заказчика будут полностью удовлетворены и мы закрываем 3-й столбец. Затем в оставшейся части таблицы (без 3-го столбца) ищем клетку с минимальным тарифом. Таких клеток две (1, 1) и (2, 4). Заполняем любую из них, например, клетку (1, 1). Остаток продукции 1-ой фабрики равен 30 – 25 = 5. Поэтому записать в клетку (1, 1) можно x 11 = min(5, 20) = 5. Поскольку с первой фабрики вывезен весь груз (30 тыс. ед.), то закрываем первую строку. Далее поступаем аналогично, заполняя свободные клетки в порядке возрастания тарифов, закрывая каждый раз нужные строку или столбец. В результате начальный план имеет вид (см. табл.1):
Проверим этот план на оптимальность. Для этого найдем потенциалы u i и v j поставщиков и потребителей. Для этого по занятым клеткам составим систему уравнений вида u i + v j = c ij:
Поскольку уравнений в системе столько же, сколько занятых клеток, то есть 7, а неизвестных - 8, то система имеет бесконечное множество решений. Положим, например, u 3 = 0. Тогда остальные потенциалы находятся однозначно: v 5 = 0; v 4 = 9; v 2 = 6; v 1 = 8; u 2 = -6; u 1 = -5; v 3 = 7. Теперь вычисляем оценки s ij свободных клеток по формуле s ij = c ij – (u i + v j):
Среди оценок есть отрицательная (s 33 = -3 < 0), следовательно план не является оптимальным. Необходимо улучшить план, загружая клетку с отрицательной оценкой. Для этого построим для клетки (3, 3) цикл с вершинами в загруженных клетках (см. табл. 1), расставляя поочередно в вершинах, начиная с клетки (3, 3), знаки «+» и «-». Из поставок в клетках, помеченных знаком «минус», выбираем наименьшую: l = min(15, 25) = 15. Для получения нового опорного плана изменим поставки в вершинах цикла: к поставкам в клетках, помеченных знаком «+», прибавляем величину l=15, в клетках, помеченных знаком «-», вычитаем эту величину 15. Новый опорный план поместим в таблицу 2. Таблица 2.
5 6 4 9 0
Исследование этого плана на оптимальность аналогично предыдущему. Вычисленные значения потенциалов записаны справа и снизу таблицы, а оценки s ij свободных клеток поместим в левых нижних углах этих клеток. Поскольку среди оценок нет отрицательных, то найденный план является оптимальным. Выписываем матрицу Х* (без последнего столбца):
Минимальные суммарные затраты по оптимальному плану составляют: Zmin = 20×3+10×2+25×3+15×6+15×4+15×9 = 430 ден. ед. Из таблицы 2 видно, что избыточная продукция в количестве 10 тыс. изд. остается на третьей фабрике.
КОНТРОЛЬНЫЕ ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ Задание 5. Определить оптимальный план перевозок с целью минимизации общих затрат на транспортировку с заданными векторами
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 251; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.191.22 (0.09 с.) |


 и
и  пары двойственных задач были их оптимальными решениями, необходимо и достаточно, чтобы они удовлетворяли системам уравнений:
пары двойственных задач были их оптимальными решениями, необходимо и достаточно, чтобы они удовлетворяли системам уравнений:
 (7)
(7) (8)
(8)
 (9)
(9)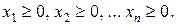 (10)
(10) являются базисными. Среди чисел
являются базисными. Среди чисел  есть отрицательные. Вектор
есть отрицательные. Вектор  есть решение системы (9). Однако, это решение не является планом задачи (8) – (10), поскольку среди его компонент есть отрицательные числе (т.е. не выполняются ограничения (10)). Исключим базисные переменные из целевой функции z:
есть решение системы (9). Однако, это решение не является планом задачи (8) – (10), поскольку среди его компонент есть отрицательные числе (т.е. не выполняются ограничения (10)). Исключим базисные переменные из целевой функции z: .
.
 l
l
 bl
bl

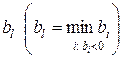 . Строка с номером l – ведущая.
. Строка с номером l – ведущая. ведущей строки l находят отрицательные. Если таковых нет, то исходная задача не имеет решения. В противном случае перейти к шагу 5.
ведущей строки l находят отрицательные. Если таковых нет, то исходная задача не имеет решения. В противном случае перейти к шагу 5. . Столбец с номером k – ведущий,
. Столбец с номером k – ведущий,  - ведущий элемент.
- ведущий элемент. есть отрицательные, то следует в системе ограничений (9) преобразовать свободные члены bj в неотрицательные, умножив на (-1) строки, содержащие отрицательные свободные члены и решать задачу (8) – (10) методом искусственного базиса.
есть отрицательные, то следует в системе ограничений (9) преобразовать свободные члены bj в неотрицательные, умножив на (-1) строки, содержащие отрицательные свободные члены и решать задачу (8) – (10) методом искусственного базиса. -x1 + 2x2 + x3 ³ 2
-x1 + 2x2 + x3 ³ 2 -y1 + 3y2 £ 6
-y1 + 3y2 £ 6 x1 - 2x2 - x3 + x4 = -2
x1 - 2x2 - x3 + x4 = -2 Из базиса будем выводить переменную x4. Следовательно, первая строка таблицы является разрешающей. Среди элементов разрешающей строки находим отрицательные а 12 = -2; a 13 = -1.
Из базиса будем выводить переменную x4. Следовательно, первая строка таблицы является разрешающей. Среди элементов разрешающей строки находим отрицательные а 12 = -2; a 13 = -1. Столбец, в котором достигается этот минимум, соответствует переменной х 3. Этот столбец является разрешающим и разрешающим элементом является элемент а 13 = -1. Это делается для того, чтобы элементы последней строки остались неотрицательными. Проводим одну итерацию метода Жордана-Гаусса относительно этого элемента, т.е. из базиса исключаем переменную х 4 и включаем в базис переменную х 3. Новая симплекс-таблица имеет вид:
Столбец, в котором достигается этот минимум, соответствует переменной х 3. Этот столбец является разрешающим и разрешающим элементом является элемент а 13 = -1. Это делается для того, чтобы элементы последней строки остались неотрицательными. Проводим одну итерацию метода Жордана-Гаусса относительно этого элемента, т.е. из базиса исключаем переменную х 4 и включаем в базис переменную х 3. Новая симплекс-таблица имеет вид:

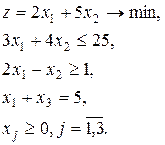








 , (14)
, (14) (15)
(15)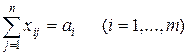 (16)
(16) (17)
(17)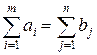 , (18)
, (18) то вводится фиктивный (n + 1) - ый пункт назначения с потребностью
то вводится фиктивный (n + 1) - ый пункт назначения с потребностью 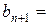
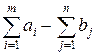 и соответствующие тарифы полагают равными нулю, т.е. c i n+1 = 0 (i = 1,2,..., m). Аналогично, при
и соответствующие тарифы полагают равными нулю, т.е. c i n+1 = 0 (i = 1,2,..., m). Аналогично, при 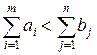 вводится фиктивный, (m+1) – ый пункт отправления с запасами груза
вводится фиктивный, (m+1) – ый пункт отправления с запасами груза  , при этом тарифы на перевозку из этого пункта также полагают равными нулю, c m+1 j = 0.
, при этом тарифы на перевозку из этого пункта также полагают равными нулю, c m+1 j = 0.
 bj
ai
bj
ai
 . Тогда в клетку (l, k) записывают число
. Тогда в клетку (l, k) записывают число  . При этом, если
. При этом, если  , то значение bk уменьшают на al и «закрывают» строку с номером l, так как ресурсы l -го поставщика исчерпаны. Если
, то значение bk уменьшают на al и «закрывают» строку с номером l, так как ресурсы l -го поставщика исчерпаны. Если  , то значение al уменьшают на bk и «закрывают» столбец с номером k, что означает удовлетворение спроса k- го потребителя. Если же al = bk, то «закрывают» строку или столбец по выбору.
, то значение al уменьшают на bk и «закрывают» столбец с номером k, что означает удовлетворение спроса k- го потребителя. Если же al = bk, то «закрывают» строку или столбец по выбору.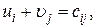
 - стоимость перевозки единицы груза занятой (базисной) клетки в i – ой строке и j -ом столбце.
- стоимость перевозки единицы груза занятой (базисной) клетки в i – ой строке и j -ом столбце. записывают справа, а потенциалы потребителей
записывают справа, а потенциалы потребителей  - внизу транспортной таблицы.
- внизу транспортной таблицы.
 , то опорный план оптимален и задача решена. В противном случае план не является оптимальным, следовательно, его нужно улучшить.
, то опорный план оптимален и задача решена. В противном случае план не является оптимальным, следовательно, его нужно улучшить.
 , где
, где  - перевозки, стоящие в вершинах цикла, отмеченных знаком «-». Величина l определяет количество груза, которое можно перераспределить по найденному циклу. Значение l записывают в незанятую клетку (l, k). Двигаясь по циклу, вычитают или прибавляют l к объемам перевозок, расположенных в клетках, помеченными знаками «-» или «+» соответственно. Перевозки в остальных базисных клетках остаются без изменения. Переходим к построению системы потенциалов.
- перевозки, стоящие в вершинах цикла, отмеченных знаком «-». Величина l определяет количество груза, которое можно перераспределить по найденному циклу. Значение l записывают в незанятую клетку (l, k). Двигаясь по циклу, вычитают или прибавляют l к объемам перевозок, расположенных в клетках, помеченными знаками «-» или «+» соответственно. Перевозки в остальных базисных клетках остаются без изменения. Переходим к построению системы потенциалов. , то вводят фиктивного поставщика
, то вводят фиктивного поставщика  или потребителя
или потребителя  или потребностями
или потребностями  соответственно. Стоимости соответствующих перевозок полагаются равными нулю. При построении начального опорного плана в этом случае фиктивные клетки заполняются в последнюю очередь.
соответственно. Стоимости соответствующих перевозок полагаются равными нулю. При построении начального опорного плана в этом случае фиктивные клетки заполняются в последнюю очередь.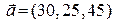 . Компания заключила договоры с четырьмя заказчиками, еженедельные потребности которых (в тыс.изделий) задаются вектором
. Компания заключила договоры с четырьмя заказчиками, еженедельные потребности которых (в тыс.изделий) задаются вектором  Стоимость транспортировки 1 тыс. изделий с i -ой фабрики j- му заказчику задается матрицей тарифов
Стоимость транспортировки 1 тыс. изделий с i -ой фабрики j- му заказчику задается матрицей тарифов  .
.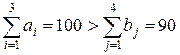 , то введем в рассмотрение фиктивного 5-го заказчика с потребностью в b 5 = 100 – 90 = 10 (тыс. ед.) груза. При этом положим c i5 = 0, i = 1, 2, 3. Исходные данные запишем в виде таблицы.
, то введем в рассмотрение фиктивного 5-го заказчика с потребностью в b 5 = 100 – 90 = 10 (тыс. ед.) груза. При этом положим c i5 = 0, i = 1, 2, 3. Исходные данные запишем в виде таблицы. bj
bj 
 +
+
 -
-

 b j
b j 
 и
и  и матрицей стоимостей С.
и матрицей стоимостей С.