
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
II. Решение задачи линейного программирования геометрическим методомСодержание книги
Поиск на нашем сайте
Общей задачей линейного программирования называется задача нахождения минимума (максимума) линейной функции
Z = c1 x1 + c2 x2 +...+ cn xn ® min (max) (1)
при ограничениях:
a21 x1 + a22 x2 +...+ a2n xn £ (=, ³) b2 (2) .................................. am1 x1 + am2 x2 +...+ amn xn £ (=, ³) bm, xj ³ 0, j = 1,..., n (3)
где cj, aij, bi - заданные числа, xj - неизвестные, i = 1,…,m, j = 1,…,n и в любом из ограничений вида (2) может встречаться любой из знаков £, = или ³. Если число неизвестных n = 2, то задача (1) – (3) примет вид
Z = c1 x + c2 y ® min (max) (4)
a21 x + a22 y £ (=, ³) b2 (5) ...................... am1 x + am2 y £ (=, ³) bm, x ³ 0, y ³ 0. (6)
и ее можно решить геометрическим методом, так как каждая пара неизвестных (х, y) может быть представлена точкой на координатной плоскости хОy. При решении задачи (4) – (6) сначала строят так называемую допустимую область, т.е. множество точек (х, y) плоскости, координаты которых удовлетворяют всем ограничениям (5) и лежат в первой четверти координатной плоскости (ограничение (6)). Поскольку все ограничения (5) – линейные, то допустимая область будет представлять собой выпуклый многоугольник (конечный или бесконечный) или пустое множество. Затем среди точек допустимой области находят оптимальную, т.е. такую точку М0 координаты которой (х0 , y0) доставляют минимум (максимум) целевой функции Z. Для этого по виду целевой функции (4) строят линию уровня функции Z, соответствующую Z=0, т.е. прямую L0: c1 x + c2 y = 0 и находят градиент функции Z – вектор Перемещая линию уровня L0 параллельно самой себе в направлении градиента (с1, с2), находим последнюю точку допустимой области, которую она пересекает при таком движении. Очевидно, что это будет точка максимума. Перемещая линию уровня в противоположном направлении (-с1, -с2), находим точку минимума. Поясним этот метод на конкретном примере. Геометрическим методом найти максимум и минимум функции Z для x, y ³ 0 при заданных ограничениях. Z = x – 3y
5x + 4y £ 34 x + 8y ³ 14 Решение. Построим допустимую область. Для этого в системе координат х0y строим прямую - x + y= 4 - границу первого ограничения. Затем определяем, в какой полуплоскости находятся точки (х, y), для которых -x + y < 4. Для этого выбираем любую точку, например (0, 0), и проверяем, удовлетворяет ли она этому неравенству. Поскольку -0 + 0 = 0 < 4, то точки, для которых - x+y£ 4 лежат в той же полуплоскости, что и точка О(0, 0), т.е. справа (ниже) от границы -x + y = 4.
L2
4 B L1
1,75 A D
x + 8y =14
Аналогично строятся остальные полуплоскости, соответствующие ограничениям 5 х + 4 у £ 34 и х + 8 у ³ 14 (ниже прямой 5 х + 4 у = 34 и выше прямой х + 8 у = 14). Множество точек, удовлетворяющих всем трем неравенствам, образуют треугольник ECD. Учитывая ограничение х ³ 0 и у ³ 0, получаем допустимую область – четырехугольник ABCD. Проведем линию уровня L 0, соответствующую значению Z =0, т.е. прямую х – 3 у = 0 (для точек, лежащих на этой прямой, значение Z =0). Она будет проходить через точку О(0, 0) перпендикулярно вектору Задача решена полностью.
КОНТРОЛЬНЫЕ ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задание 2. Геометрическим методом найти максимум и минимум функции Z для x, y ³ 0 при заданных ограничениях:
Варианты:
1. Z = 2x + y 2. Z = 3x + y
-x + 6y £ 8 x - 2y £ 3 x + y ³ 1 2x + y ³ 1
3. Z = 2x - y 4. Z = x + y
x + y ³ 6 x + y £ 7 x - 3y £ 3 -x + 2y £ 2
5. Z = 4x + y 6. Z = 3x - y
4x - y £ 14 x ³ 2 3x + y ³ 7 5x - 3y £ 22
7. Z = 2x + y 8. Z = x + 5y
4x - y £ 8 x - y £ 4 x - y ³ -1 x + y ³ 6
9. Z = 5x + y 10. Z = 3x
4x - 3y £ 14 2x - y £ 11 3x + y ³ 4 4x + y ³ 19
|
||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.19.89 (0.005 с.) |

 a11 x1 + a12 x2 +...+ a1n xn £ (=, ³) b1
a11 x1 + a12 x2 +...+ a1n xn £ (=, ³) b1 a11 x + a12 y £ (=, ³) b1
a11 x + a12 y £ (=, ³) b1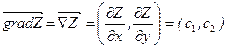 , который показывает направление наибыстрейшего возрастания функции Z. Вектор антиградиента (-с1, -с2) будет показывать направление наибыстрейшего убывания целевой функции Z. Вектор градиента перпендикулярен линии уровня L0.
, который показывает направление наибыстрейшего возрастания функции Z. Вектор антиградиента (-с1, -с2) будет показывать направление наибыстрейшего убывания целевой функции Z. Вектор градиента перпендикулярен линии уровня L0. -x + y £ 4
-x + y £ 4 y
y

 8,5 -x + y = 4
8,5 -x + y = 4 C
C L0
L0 E
E

 0 1 6,8 14 y
0 1 6,8 14 y -3
-3  5x + 4y = 34
5x + 4y = 34 . Перемещая линию уровня в направлении градиента
. Перемещая линию уровня в направлении градиента 
 3x - 4y £ 4 y £ 1
3x - 4y £ 4 y £ 1
 2x + y £ 3 y ³ 2
2x + y £ 3 y ³ 2
 x - 2y ³ 0 2x + 3y £ 13
x - 2y ³ 0 2x + 3y £ 13
 x ³ 2 3x - y ³ 3
x ³ 2 3x - y ³ 3
 x - 4y ³ -3 x + y £ 7
x - 4y ³ -3 x + y £ 7


