
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм приведения матрицы к базисному виду
Каждая итерация алгоритма состоит из трех шагов: Шаг 1. В первой строке матрицы находим ненулевой элемент a 1j¹ 0, (желательно, a 1j = 1). Если таких нет, то в случае b 1 = 0 вычеркиваем нулевую строку; если b 1 ≠ 0, то, очевидно, система несовместна. Найденный элемент назовем разрешающим (или ведущим). Если a 1j = 1, то переходим к шагу 3, иначе к шагу 2. Шаг 2. Делим первую строку на разрешающий элемент a 1j ≠ 0. (После этого шага коэффициент при x j в первом уравнении будет a 1j = 1) Шаг 3. Ко всем остальным строкам, кроме первой, прибавляем первую строку, умноженную на (- a ij), где i - номер изменяемой строки (i = 2,3,…, m). После этого шага коэффициент при x j в остальных уравнениях будет 0, и переменная x j станет базисной в первом уравнении. Затем применяем шаги 1, 2 и 3 ко второму уравнению полученной матрицы и т.д. Так как число уравнений системы конечно, то этот процесс завершится не более чем за m итераций. Решение системы по этому алгоритму называется методом Жордана-Гаусса. После того, как система приведена к базисному виду, находят базисное решение, соответствующее выбранному базису. Для этого переменные, не вошедшие в базис, приравнивают нулю, а остальные переменные (базисные) находят по правым частям соответствующих уравнений. Приведем решение типового примера задания 1: Найти базисное решение системы с расширенной матрицей
Применим алгоритм приведения матрицы к базисному виду: В первой строке элемент a12 =1, поэтому выберем его в качестве разрешающего. Теперь изменяем вторую и третью строки следующим образом: ко второй строке прибавляем первую, умноженную на (-2), к третьей прибавляем первую, умноженную на (-5). В результате получим матрицу
в которой переменная x2 стала базисной в первом уравнении. Теперь применяем шаги 1-3 ко второй строке полученной матрицы. Находим ненулевой элемент, например, a24 = 3, и делим вторую строку на этот элемент. Получим матрицу
Теперь делаем нули в остальных строках четвертого столбца этой матрицы, для чего к первой строке прибавляем вторую, умноженную на -1, к третьей прибавляем вторую, умноженную на -9. В результате расширенная матрица системы примет вид:
Вычеркивая нулевую третью строку, получим матрицу, в базисном виде:
В первой строке базисной является переменная x2, а во второй – переменная x4. Переменные x1 и x3 являются свободными. Приравнивая их нулю, получаем базисное решение, соответствующее этому базису: x1 = x3 = 0, x2 =8/3, x4 = 4/3 или Х1 = (0, 8/3, 0, 4/3). Найдем другое базисное решение, т.е. решение, в котором базисными являются другие переменные. В базис можно включить переменные x1 или x3, которые сейчас являются свободными. Выберем, например, переменную x1 для включения в базис. Ее можно сделать базисной в первой строке, т.к. элемент а11 = 8/3 ≠ 0 (при этом из базиса выйдет переменная x2), или во второй строке а21 = -2/3 ≠ 0 (при этом из базиса выйдет х4). Будем делать x1 базисной, например, в первой строке, т.е. в качестве разрешающего выберем элемент а11 = 8/3 ≠ 0 (помечен в последней матрице). Как и раньше, разделив первую строку на разрешающий элемент и прибавив ко второй строке полученную первую, умноженную на 2/3, приведем матрицу к новому базису:
Полагая свободные переменные x2 и x3 равными нулю, получим новое базисное решение Х2 = (1, 0, 0, 2).
Контрольные задания для самостоятельного решения Задание 1. Найти целочисленное базисное решение системы с заданной расширенной матрицей:
Варианты:
-3 3 -2 4 1 3 0 3 -2 12 0 1 0 3 -1 -3 4 0 -1 2
3 3 -4 1 12 0 3 3 1 0 11 -3 2 5 30 2 9 5 7 -4
0 1 3 2 6 1 1 1 -1 -3 1 0 -1 1 -3 3 1 -2 -1 -13
3 -1 -1 1 -7 0 2 -3 2 1 2 -2 -3 2 0 3 4 -1 3 10
-3 4 4 0 -20 -1 1 1 2 6 2 -3 1 -4 7 2 4 -3 0 2
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 466; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.97.157 (0.008 с.) |


 ,
,


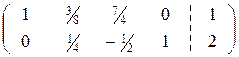




 1. 0 1 0 –1 -1 2. 2 2 0 1 8
1. 0 1 0 –1 -1 2. 2 2 0 1 8

 3. 4 -3 3 2 9 4. 1 3 1 3 -2
3. 4 -3 3 2 9 4. 1 3 1 3 -2


 5. 1 0 1 1 3 6. 4 -3 1 1 3
5. 1 0 1 1 3 6. 4 -3 1 1 3


 7. -2 2 -3 4 12 8. 0 3 4 2 10
7. -2 2 -3 4 12 8. 0 3 4 2 10



 9. 0 2 0 -1 -6 10. 2 -2 3 -1 8
9. 0 2 0 -1 -6 10. 2 -2 3 -1 8


