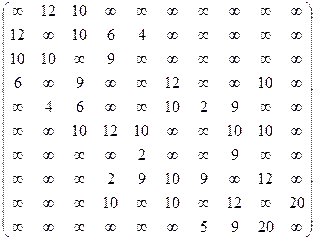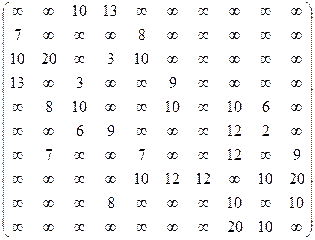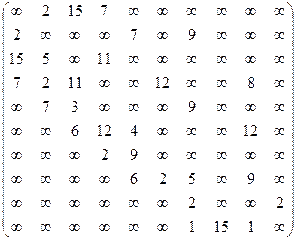Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм построения кратчайших путей в сети ⇐ ПредыдущаяСтр 9 из 9
Начальный шаг. Полагаем l*(s): = 0, R: = { s }, l(j) = lsj, если дуга (s, j) Î U и l(j) = ¥ в противном случае. Для всех вершин v(j) = s. Общая итерация. Шаг 1. Пусть arg( Если l (k) < ¥ полагаем R: =R È {i} и l*(i)= l(i), v*(i)= k. Если R = V - алгоритм заканчивает работу. Если R ¹V - переходим к шагу 2. Шаг 2. Для всех j Ï R, таких, что (k, j) Î U полагаем l(j): = Если l(i) + lij < l(j), то v(j): = i; в противном случае v(j) не меняется. Переходим к шагу 1 следующей итерации. Рассмотрим итерацию, на которой алгоритм заканчивает работу. Это происходит на шаге 1, когда либо l(j) = ¥ для всех j Ï R и R ¹ V, либо R=V. В первом случае ни одна дуга, начальной вершиной которой являются вершина множества R, не ведет в вершины, не принадлежащие этому множеству, а значит, не существует путей, ведущих из вершины s в вершины, не принадлежащие множеству R. Во втором случае все вершины получили постоянную метку (l*(i), v*(i)), т.е. найдены кратчайшие расстояния от вершины S ко всем остальным вершинам сети. Заметим, что алгоритм явно не указывает кратчайший путь к вершине, а только его длину. Но воспользовавшись второй частью метки: v*(i) - его легко восстановить. Действительно, v*(i) - номер предпоследней вершины в кратчайшем пути из S в i; пусть v*(i) = i1. Но v*(i1) = i2 - номер предпоследней вершины в кратчайшем пути из S в i1. Продолжая, мы найдем последовательность вершин S, ik, ik-1,..., i2, i1, k, через которые проходит кратчайший путь. Рассмотрим работу алгоритма на следующем примере. Найти кратчайшие пути из вершины S во все остальные вершины сети, изображенной на рис.7 (числа над дугами равны их длинам).
Рис.7
На начальном плане вершина S получает постоянную метку (0*, S *), R = { S }, соседние с ней вершины 1, 2, 3 получают временные метки (1, S), (10, S) и (6, S) соответственно, а остальные вершины получают временные метки (¥, S) (рис.8 ).
Рис. 8 Итерация 1. 1) Минимальное значение первой части меток всех вершин равно 1 для первой вершины, т.е. arg( 2) Просматриваем все вершины, соседние с вершиной, получившей постоянную метку (вершиной 1). Для вершины 5 имеем l*(1) + l15 =1 + 2 = 3 < l(5) = ¥, поэтому полагаем l(5) = 3, V(5) = 1.
Для вершины 2 имеем min(l*(1) + l12, l*(S) + l32 = min (1 + ¥, 10) = 10. Так как l(2) = 10, то метка вершины 2 не меняется. Переходим ко второй итерации и т.д. Заметим, что на каждой итерации алгоритма одна очередная вершина i присоединяется к множеству R и получает постоянную метку (l*(i), v*(i)), которая в дальнейшем не меняется, а для остальных вершин j Ï R пересматриваются текущие значения величин l (j), некоторые из которых могут меняться и в дальнейшем. Результаты вычислений на начальном шаге (итерация 0) и на всех последующих итерациях удобно заносить в таблицу 2.1. Если пара чисел (l (i), v(i)) помечается символом (*), это означает, что вершина i получила постоянную метку (l*(i), v*(i)), которая в дальнейшем не меняется.
Таблица 2.1
Алгоритм закончил работу на 7-й итерации случаем, когда R = {s, 1, 2, 3, 4, 5, 7, t }, {6 } Ï R и R ¹ V, а l(6) = ¥. Это означает, что не существует пути, ведущего из вершины s в вершину 6. Для всех остальных вершин сети длины кратчайших путей найдены, а сами пути могут быть построены, как описано выше. Например, для вершины 2 имеем: (l*(2), v*(2)) = (7*, 3*); предыдущая вершина кратчайшего пути - 3. Для вершины 3 (l*(3), v*(3)) = (6*, 4*); для вершины 4 - ((l*(4), v*(4)) = (4*, 5*); для вершины 5 - ((l*(5), v*(5)) = (3*, 1*); а для вершины 1 - ((l*(1), v*(1)) = (1*, s*). Таким образом, кратчайший (s - 2) путь проходит через вершины s, 1, 5, 4, 3, 2 и его длина равна 7. Все дуги сети, входящие в кратчайшие пути, изображены на рис.9. Пары чисел около вершин (рис.8, 9) - это найденные в результате работы алгоритма постоянные метки вершин, первая часть которых l*(i) - длина кратчайшего (s - i) пути P*(s, i), а вторая - предпоследняя вершина этого пути (последней является вершина i). Кратчайшие пути образуют дерево, но не остовное, так как вершина 6 не соединена ни с одной другой вершиной.
Рис. 9
В заключение отметим, что поскольку на каждой итерации алгоритма только одна новая вершина и соответствующая дуга добавляются к множеству дуг и вершин, образующих кратчайшие пути, то отсюда следует, что множество кратчайших путей в любой сети образует дерево (т.е. не содержит цикла).
КОНТРОЛЬНЫЕ ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
Задание 8. Дана матрица
ЛИТЕРАТУРА
1. Кузнецов А.В., Холод Н.И. Математическое программирование. – Мн., Вышэйшая школа, 1984. 2. Балашевич В.А. Математические методы в управление производством. – Мн., Вышэйшая школа, 1976. 3. Банди Б. Основы линейного программирования. – М., Радио и связь, 1988. 4. Банди Б. Методы оптимизации. Вводный курс. – М., Радио и связь, 1989. 5. Калихман И.Л. Сборник задач по математическому программированию. – М., Высшая школа, 1975. 6. ЕмеличеваЕ.В., Еровенко Л.Д., Корзников А.Д., Ласый П.Г. Сборник задач и методические указания к решению задач по математическому программированию. – Мн., ротапринт БГПА, 1996. 7. Гайков Н.Е., Емеличева Е.В., Корзников А.Д., Павлов В.В., Смирнов М.Б. Математические методы в технико-экономических задачах. – Мн., ротапринт БПИ, 1991.
СОДЕРЖАНИЕ Стр.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-21; просмотров: 560; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.112.111 (0.014 с.) |
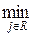 l(j)) = i и вершина i имеет метку (l(i), k). Если l(k) = ¥ и R ¹ V - алгоритм заканчивает работу.
l(j)) = i и вершина i имеет метку (l(i), k). Если l(k) = ¥ и R ¹ V - алгоритм заканчивает работу.
 ) = 1. Метка первой вершины становится постоянной. Полагаем R:= R
) = 1. Метка первой вершины становится постоянной. Полагаем R:= R  {1} = {S, 1}, переходим к шагу 2.
{1} = {S, 1}, переходим к шагу 2. Вершина
итерация
Вершина
итерация

 расстояний между каждой парой вершин сети. Если
расстояний между каждой парой вершин сети. Если  , это означает, что в сети нет дуги, ведущей из вершины i в вершину j. Если
, это означает, что в сети нет дуги, ведущей из вершины i в вершину j. Если 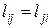 , то вершины i и j соединены неориентированной дугой длины
, то вершины i и j соединены неориентированной дугой длины 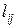 . Требуется по матрице L построить сеть и найти кратчайшие пути из вершины 1 во все остальные вершины сети.
. Требуется по матрице L построить сеть и найти кратчайшие пути из вершины 1 во все остальные вершины сети.