
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Экстремум функции нескольких переменных. 56.Необходимые и достаточные условия существования безусловного экстремума.Содержание книги
Поиск на нашем сайте
Определение. Точка (x 0, y 0) называется точкой локального максимума (минимума) функции, если найдется некоторая окрестность данной точки, для всех точек которой выполняется условие Теорема (необходимое условие экстремума функции). Если точка (x 0, y 0) является точкой локального экстремума функции, то в этой точке частные производные равны нулю или не существуют. Теорема (достаточное условие экстремума функции). Пусть функция z=f(x,y) определена в некоторой окрестности критической точки (x 0, y 0), в которой частные производные равны нулю: Тогда если D= AC-B 2>0, то в точке (x 0, y 0) функция имеет экстремум, причем если А <0 - максимум, если А >0 - минимум. В случае D= AC - B 2<0 функция экстремума не имеет. Если D= AC-B =0, то вопрос о наличии экстремума остается открытым.
Первообразная. Определение. Первообразной функцией F(x) дляфункции f(x) называется функция,производная которой равна исходной функции.(F (x))' = f (x). Теорема (теоремаКоши). Любая непрерывная на некотором множестве функция имеет на этом множестве первообразную. Теорема. Если F 1 (x) и F 2 (x) - две первообразные для функции f(x), то они отличаются на постоянное слагаемое. Неопределенный интеграл и его свойства. Определение. Совокупностьвсех первообразных данной непрерывной функции называется неопределенным интегралом от этой функции и обозначается ò f(x)dx,где f(x) именуется подынтегральной функцией, выражение f(x)dx - подынтегральным выражением.Если F(x) - некоторая первообразная данной функции, тоò f(x)dx = F(x) + C, где C - произвольная постоянная.Процесс нахождения неопределенного интеграла называется интегрированием данной функции, или взятием интеграла от данной функции. Теорема1. Производная от неопределенного интеграла равна подынтегральной функции,дифференциал от неопределенного интеграла равен подынтегральному выражению. (ò f(x)dx) ' = (F(x) + c)' = f(x),d (ò f(x)dx) = (ò f(x)dx) ' dx = f(x)dx. Теорема 2. Интеграл от дифференциала функции равен этой функции с точностью до постоянного слагаемого. Доказательство. ò d f(x) = ò f'(x)dx = f(x) + C. Из теорем 1 и 2 следует, что операции дифференцирования и интегрированияявляются взаимнообратными.
Теорема 3. Постоянный множитель можно выносить за знак интеграла. Теорема 4. Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 301; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.45.228 (0.007 с.) |

 (
(  ).Точки локального максимума и минимума называются точками экстремума.
).Точки локального максимума и минимума называются точками экстремума. ,
,  ;в этой точке функция имеет непрерывные частные производные второго порядка
;в этой точке функция имеет непрерывные частные производные второго порядка  ,
, 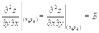 ,
,  .
.


