
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциал функции. Геометрический смысл дифференциала.Содержание книги
Поиск на нашем сайте Определение. Главная линейная относительно D х часть малого приращения функции называется дифференциалом функции и обозначается dy. Если малое приращение функции можно представить в виде Геометрический смысл дифференциала
Y B
f(x 0 +Dx) f(x 0 ) A a D
0 x 0 x 0 +Dx Х
Рассмотрим D ABD: Дифференциал функции в точке равен приращению ординаты касательной, проведенной к графику функции в данной точке.
Возрастание и убывание функций. Точки экстремума. Определение. Числоваяфункция y=f(x) называется монотонно возрастающей (убывающей) на множестве АÌ D(f), если большему значению аргумента соответствует большее (меньшее) значение функции: "x 1, x 2 ÎАÌ D(f): x 1 >x 2 Þf(x 1 )>f(x 2 ) (f(x 1 )<f(x 2 )). Из определения следует, что если функция возрастает (убывает), то
Приращение функции и приращение аргумента возрастающей (убывающей) функции имеют одинаковые (противоположные) знаки. Теорема1. Если дифференцируемая функция возрастает (убывает) на некотором интервале, то в каждой точке этого интервала производная этой функции неотрицательна (неположительна). Теорема2. Если производная функции на некотором интервале неотрицательна (неположительна), то на этом интервале функция возрастает (убывает). Необходимое условие существования экстремума. Если дифференцируемая функция у=ƒ(х) имеет экстремум в точке х0, то ее производная в этой точке равна нулю: ƒ'(х0)=0.Пусть, для определенности, x0 — точка максимума. Значит, в окрестности точки х0 выполняется неравенство ƒ(х0)>ƒ(х0+∆х). Но тогда
Критические точки. Достаточные условия существования экстремума. Непрерывная функция может иметь экстремум лишь в точках, где производная функции равна нулю или не существует. Такие точки называются кри тическими. Достаточные условия существования экстремума. Если непрерывная функция у=ƒ(х) дифференцируема в некоторой d -окрестности критической точки х0 и при переходе через нее (слева направо) производная ƒ'(х) меняет знак с плюса на минус, то х0 есть точка максимума; с минуса на плюс, то х0 — точка минимума.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 438; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.151.52 (0.008 с.) |

 , где
, где 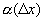 - б.м. функция более высокого порядка, чем D х при
- б.м. функция более высокого порядка, чем D х при 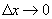 (
( 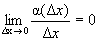 ), тогда
), тогда 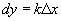 .
. Дана дифференцируемая функция y=f(x). Возьмем произвольную точку x 0 и проведем в этой точке касательную к графику. Дадим аргументу приращение
Дана дифференцируемая функция y=f(x). Возьмем произвольную точку x 0 и проведем в этой точке касательную к графику. Дадим аргументу приращение
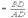 ,
, ,
, ,
, .
. ,если ∆х>0, и ∆у/∆х>0, если ∆х<0.
,если ∆х>0, и ∆у/∆х>0, если ∆х<0. По условию теоремы производная
По условию теоремы производная  существует. Переходя к пределу, при ∆х→0, получим ƒ'(x0)≥0, если ∆х<0, и f'(х0)≤0, если ∆х>0. Поэтому ƒ'(х0)=0. Аналогично доказывается утверждение теоремы, если х0 — точка минимума функции ƒ(х).
существует. Переходя к пределу, при ∆х→0, получим ƒ'(x0)≥0, если ∆х<0, и f'(х0)≤0, если ∆х>0. Поэтому ƒ'(х0)=0. Аналогично доказывается утверждение теоремы, если х0 — точка минимума функции ƒ(х).


