
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Угол между прямыми на плоскости.
Определение. Углом между двумя прямыми I и II называется угол, отсчитываемый в положительном направлении от прямой I к прямой II.
Найдем угол между первой и второй прямыми. Обозначим углы наклона прямых j 1 и j 2. Тогда k 1 = tg j 1 , k 2 = tg j 2.
- формула для вычисления угла между двумя прямыми.
23.Эллипс. Каноническое уравнение. Геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, называется эллипсом. Гипербола. Каноническое уравнение. Геометрическое место точек, разность расстояний от каждой из которых до двух данных точек, называемых фокусами, есть величина постоянная, называется гиперболой. Парабола. Каноническое уравнение. Геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой, именуется параболой. Пределы функций, их свойства. Число A называется пределом функции f (x) при x → x 0 (или в точке x 0), если для любого ε > 0 найдется δ > 0 такое, что для всех x, для которых 0 < | x − x 0| < δ, справедливо неравенство | f (x) − A | < ε, т.е. 1) Предел постоянной величины Предел постоянной величины равен самой постоянной величине: 2) Предел суммы Предел суммы двух функций равен сумме пределов этих функций:
Аналогично предел разности двух функций равен разности пределов этих функций. 3) Предел произведения функции на постоянную величину Постоянный коэффициэнт можно выносить за знак предела: 4) Предел произведения Предел произведения двух функций равен произведению пределов этих функций:
5) Предел частного Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю: Основные теоремы о пределах
Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x), то предел функции f(x) в этой точке не превосходит предела функции g(x). Теорема 3. Предел постоянной равен самой постоянной. Теорема 4. Функция не может иметь двух различных пределов в одной точке. Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при Теорема 7. Если функции f(x) и g(x) имеют предел при Замечательные пределы Теорема 1. Предел отношения синуса малой дуги к самой дуге, выраженной в радианах, при стремлении величины дуги к нулю равен единице.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.127.141 (0.007 с.) |
 Пусть даны две прямые, заданные уравнениями с угловыми коэф. y = k 1 · x + b 1, y = k 2 · x + b 2.
Пусть даны две прямые, заданные уравнениями с угловыми коэф. y = k 1 · x + b 1, y = k 2 · x + b 2.
 - каноническое уравнение эллипса.
- каноническое уравнение эллипса. - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.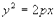 - каноническое уравнениепараболы с вершиной в начале координат, симметричной относительно оси OX.
- каноническое уравнениепараболы с вершиной в начале координат, симметричной относительно оси OX. Свойства пределов функции
Свойства пределов функции




 Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.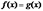 ,
, 
 .
. ,
, 
 .
.
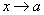 , то и алгебраическая сумма имеет предел при
, то и алгебраическая сумма имеет предел при 
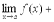
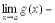
 .
.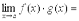

 .
.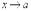 ,причем
,причем  , то и их частное имеет предел при
, то и их частное имеет предел при  ,
,  .
. .
. Теорема 2. Предел последовательности при
Теорема 2. Предел последовательности при  равен.
равен.  ,.
,.


