
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Обратная матрица. Теорема о существовании обратной матрицы.Стр 1 из 7Следующая ⇒
Определители и их свойства
2. Миноры и алгебраические дополнения Пусть дана матрица А размера mxn Определение. Минором порядка k данной матрицы,где k Вычисление определителей порядка n >3 сводится к вычислению определителей второго и третьего порядка с помощью теоремы 1 и свойства 5 определителя.
3. Методы вычисления определителей. Определение 1. Определителем n -го порядка матрицы А называется число, равное алгебраической сумме n! слагаемых, каждое из которых равно произведению n элементов матрицы А
, Системы линейных уравнений Определение 1. Система вида Метод Гаусса. Метод Гаусса - это универсальный метод исследования и решения произвольных систем линейных уравнений. Он состоит в приведении системы к диагональному виду путем последовательного исключения неизвестных с помощью элементарных преобразований, не нарушающих эквивалентности систем. Переменная считается исключенной, если она содержится только в одном уравнении системы с коэффициентом 1. Перейдем теперь к решению систем с различным количеством неизвестных и уравнений. Пусть дана система m линейных уравнений с n неизвестными. Если такая система совместна, то при r<n она имеет бесконечное множество решений, каждое из которых может быть получено из общего решения системы.
Для нахождения общего решения нам необходимо выбрать, какие неизвестные мы будем считать основными (базисными). Это могут быть любые r переменных, коэффициенты при которых составляют определитель, отличный от нуля. Затем выбранные основные переменные нужно выразить через свободные. Для этого с помощью элементарных преобразований необходимо расширенную матрицу системы привести к такому виду, чтобы коэффициенты при базисных переменных образовали так называемые базисные столбцы - столбцы, состоящие из нулей и одной единицы. Решение систем линейных уравнений методом последовательного исключения неизвестных можно оформлять в виде таблицы. Левый столбец таблицы содержит информацию об исключенных (базисных) переменных. Остальные столбцы содержат коэффициенты при неизвестных и свободные члены уравнений. В исходную таблицу записывают расширенную матрицу системы. Далее приступают к выполнению очередной итерации: 1. Выбирают переменную 2. Элементы ключевой строки делят на ключевой элемент. 3. Ключевой столбец заполняют нулями. 4. Остальные элементы вычисляют по правилу прямоугольника: составляют прямоугольник, в противоположных вершинах которого находятся ключевой элемент и пересчитываемый элемент; из произведения элементов, стоящих на диагонали прямоугольника с ключевым элементом, вычитают произведение элементов другой диагонали и полученную разность делят на ключевой элемент. Общее уравнение плоскости. Определение. Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению: Ax + By + Cz + D = 0, где А, В, С – координаты вектора -вектор нормали к плоскости. Основные теоремы о пределах
Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x), то предел функции f(x) в этой точке не превосходит предела функции g(x). Теорема 3. Предел постоянной равен самой постоянной. Теорема 4. Функция не может иметь двух различных пределов в одной точке. Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при Теорема 7. Если функции f(x) и g(x) имеют предел при Замечательные пределы Теорема 1. Предел отношения синуса малой дуги к самой дуге, выраженной в радианах, при стремлении величины дуги к нулю равен единице.
Точки разрыва функции Функция является непрерывной в точке, если Определение. Точки, в которых нарушается условие непрерывности, называют точками разрыва функции. Определение. Точка разрыва х 0 называется точкой разрыва первого рода, если существуют конечные односторонние пределы в этой точке. Определение. Точка х 0 называется точкой разрыва второго рода, если она не является точкой разрыва первого рода (если хотя бы один из односторонних пределов не существует или равен +¥(-¥)). Асимптоты Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.Говорят, что прямая х=а является вертикальной асимптотой графика функции
46. Функции нескольких переменных (Определение, примеры). Пусть даны множества D - Полный дифференциал. Полным дифференциалом функции z=f (x, y) называется главная часть полного приращения функции D z, линейная относительно D х и D у, то есть dz= f’x (x, y) dx + f’y (x, y) dy или dz=
Первообразная. Определение. Первообразной функцией F(x) дляфункции f(x) называется функция,производная которой равна исходной функции.(F (x))' = f (x). Теорема (теоремаКоши). Любая непрерывная на некотором множестве функция имеет на этом множестве первообразную. Теорема. Если F 1 (x) и F 2 (x) - две первообразные для функции f(x), то они отличаются на постоянное слагаемое. Формула Ньютона-Лейбница. Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной. Пусть функция f (x) непрерывна на [ a; b ], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда
Для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a). 73.Приложения определенного интеграла к решению геометрических и механических задач. 1. Вычисление площадей фигур, расположенных под (над) графиком функции на некотором отрезке. Это приложение вытекает из геометрического смысла определенного интеграла S =
Длина дуги кривой. Если плоская кривая задана уравнением y=f(x) её длина равна:
Если дуги пространственной кривой заданы параметрически уравнениями x= x(t), y=y(t), z= z(t) при изменении t от а до b имеем:
Вычисление объема тела. Пусть требуется найти объем V тела, причем известны площади S сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ох: S = S(x), а ≤ х ≤ b.
Объем тела вращения. Вычисление объема тела сводится также к вычислению определенного интеграла. Пусть рассматриваемое тело Е получается от вращения данной кривой y=f(x), заданной на сегменте [a,b], вокруг оси Ох. Обозначим через V объем данного тела. Разобьем тело поперечными сечениями, перпендикулярными к оси Ох, начиная от х=а и кончая х=b.
Очевидно поперечные сечения - круги радиуса у. Рассмотрим один из элементов Е, образованный сечениями с абсциссами х и х + х. Будем считать, что х достаточно мало и заменим объем тела Е объемом прямого цилиндра, высота которого x,а площадь основания S(x) = П f 2(x) и, следовательно, для объема V тела получим приближенное выражение
Теорема. Объем тела, получаемого при вращении вокруг оси Ох кривой y=f(x), заключенный между ординатами х=а и х=b, выражается формулой
Двойной интеграл. Двойным интегралом называют кратный интеграл с d=2.
В прямоугольных координатах: Числовой ряд, сумма ряда. Пусть дана последовательность действительных положительных чисел
Формулы Крамера Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно). Описание метода
с определителем матрицы системы Δ, отличным от нуля, решение записывается в виде (i-ый столбец матрицы системы заменяется столбцом свободных членов).
В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:
В этой форме формула Крамера справедлива без предположения, что Δ отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов).
19. Параметрическое и каноническое уравнение прямой. Пусть прямая проходит через точку M 1 (x 1, y 1, z 1) и параллельна вектору Пусть прямая проходит через две точки M 1 (x 1, y 1, z 1) и M 2(x 2, y 2, z 2).Составим ее уравнение. 26. Функция. Характеристики поведения. Сложная функция. Пусть Х и Y - некоторые множества. Определение. Если каждому элементу x Î Х ставится в соответствие по некоторому правилу единственный элемент y Î Y, то говорят, что на множестве Х задана функция (отображение) со значениями в множестве Y: f: X®Y, y=f(x). Множество Х называется областью определения функции и обозначается Dom (f) или D (f), множество Y называется множеством значений функции и обозначается Im(f) или I(f). Основные характеристики функции 1. Функция у=ƒ(х), определенная на множестве D, называется четной, если " xÎ D выполняются условия -хєD и ƒ(-х)=ƒ(х); нечетной, если " xєD выполняются условия -хєD и ƒ(-х)=-ƒ(х).График четной функции симметричен относительно оси Оу, а нечетной — относительно начала координат.2. Пусть функция у=ƒ(х) определена на множестве D и пусть D 1єD. Если для любых значений х 1;x2єD1 аргументов из неравенства x1<x2 вытекает неравенство: ƒ(x 1)<ƒ(х2), то функция называется возрастающей на множестве D 1; f(x1) ≤ ƒ(х2), то функция называется неубывающей на множестве D1; f(x1)>ƒ(х2), то функция называется убывающей на множестве D1; ƒ(х1)≥ƒ(x2), то функция называется невозрастающей на множестве D1. Пусть функция у=ƒ(u) определена на множестве D, а функция u= φ(х) на множестве D1, причем для " xÎ D1соответствующее значение u=φ(х) є D. Тогда на множестве D 1 определена функция u=ƒ(φ(х)), которая называется сложной функцией от х (или суперпозицией заданных функций, или функцией от функции).Переменную u=φ(х) называют промежуточным аргументом сложной функции.
35. Дифференцирование тригонометрических и обратных им функций.
Формула Тейлора. Пусть функция ƒ(х) есть многочлен Рn(х) степени n:ƒ(х)=Рn(х)=а0+а1х+а2х2+...+аnхn.Преобразуем этот многочлен также в многочлен степени n относительно разности х-х0, где х0 — произвольное число, т. е. представим Рn(х) в видеРn(х)=А0+A1(x-х0)+А2(х-х0)2+...+Аn(х-х0)n (.1)Для нахождения коэффициентов А0, А1,..., Аn продифференцируем n раз равенство (1): Р'n(х)=А1+2А2(х-x0)+3A3(x-x0)2+...+nAn(x-x0)n-1, Рn''(х)=2А2+2•3А3(х-х0)+...+n(n-1)Аn(х-х0)n-2, Рn"'(х)=2•3А3+2•3•4А4(х-х0)+...+n(n-1)(n-2)Аn(х-х0)n-3, - - - - - - - - - - - - - - - - - - Рn(n)(х)=n(n-1)(n-2)...2•1Аn Подставляя х=х0 в полученные равенства и равенство (.1), имеем:
Подставляя найденные значения A0,A1,...,An в равенство (.1), получим разложение многочлена n-й степени Рn(х) по степеням (х-х0):
54. Формула Тейлора для функции нескольких переменных. Пусть функция f(x) задана в области R и имеет в R все частные производные до порядка m+1 включительно. Пусть
При m=1 получается линейное приближение функции f: При m=2 получается квадратичное приближение функции f:
Определители и их свойства
2. Миноры и алгебраические дополнения Пусть дана матрица А размера mxn Определение. Минором порядка k данной матрицы,где k Вычисление определителей порядка n >3 сводится к вычислению определителей второго и третьего порядка с помощью теоремы 1 и свойства 5 определителя. 3. Методы вычисления определителей. Определение 1. Определителем n -го порядка матрицы А называется число, равное алгебраической сумме n! слагаемых, каждое из которых равно произведению n элементов матрицы А
, Обратная матрица. Теорема о существовании обратной матрицы. Определение. Матрица А -1 называется обратной к квадратной матрице А n -го порядка, если А · А -1= А -1· А = Е. Для любой невырожденной квадратной матрицы существует единственная обратная матрица. Доказательство. 1 часть (единственность). Предположим, что обратная матрица существует. Докажем, что она единственная. Предположим противное, т.е. существует две обратные матрицы: А -1 и 2 часть (существование). Дана матрица An*n. Построим обратную матрицу. Для этого совершим ряд действий:1) заменим все элементы матрицы их алгебраическими дополнениями:2) транспонируем полученную матрицу:3) разделим все элементы на число ½ А ½Проверим, будет ли полученная матрица обратной к исходной. Для этого умножим матрицу А на А -1. Элемент, стоящий в i -й строке и j -м столбце матрицы произведения, будет равенЭлементы матрицы-результата совпадают с элементами единичной матрицы Е. Следовательно, А · А -1= Е, т.е. А -1 - обратная матрица к А. 5.Элементарные преобразования матрицы. Определение. Элементарными преобразования-минад матрицей называются: 1) умножение любой строки на число, отличное от нуля; 2) прибавление к элементам одной строки соответствующих элементов другой, умноженных на одно и то же число;3) перестановка строк; 4) отбрасывание строки из нулей. Определение. Две матрицы называются эквивалентными (А ~ В), если от одной можно перейти к другой с помощью конечного числа элементарных преобразований.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.202.187 (0.122 с.) |
 Пусть дана квадратная матрица порядка n Определение. Определителем n -го порядка матрицы А называется число, равное алгебраической сумме n! слагаемых, каждое из которых равно произведению n элементов матрицы А, взятых по одному из каждой строки и каждого столбца, причем каждое слагаемое берется со знаком "+" или "-".
Пусть дана квадратная матрица порядка n Определение. Определителем n -го порядка матрицы А называется число, равное алгебраической сумме n! слагаемых, каждое из которых равно произведению n элементов матрицы А, взятых по одному из каждой строки и каждого столбца, причем каждое слагаемое берется со знаком "+" или "-". . Свойства определителей: 1. При транспонировании величина определителя не меняется.. 2. Если все элементы одной строки определителя умножить на одно и то же число, то и весь определитель умножится на это число. Следствие. Постоянный множитель строки можно выносить за знак определителя. 3. Если в определителе поменять местами две строки, то определитель сменит знак на противоположный. Следствие 1. Определитель, у которого две строки равны, равен нулю. Следствие 2. Если в определителе две строки пропорциональны, то такой определитель равен нулю. 4. Если строка определителя представлена в виде алгебраической суммы нескольких слагаемых, то определитель равен алгебраической сумме определителей, у которых в первом определителе в данной строке стоит первое слагаемое, во втором - второе слагаемое и т.д. Следствие. Если строки определителя линейно зависимы, то такой определитель равен нулю. 5. Если к элементам одной строки определителя прибавить соответствующие элементы другой, умноженные на одно и то же число, то определитель не изменится.
. Свойства определителей: 1. При транспонировании величина определителя не меняется.. 2. Если все элементы одной строки определителя умножить на одно и то же число, то и весь определитель умножится на это число. Следствие. Постоянный множитель строки можно выносить за знак определителя. 3. Если в определителе поменять местами две строки, то определитель сменит знак на противоположный. Следствие 1. Определитель, у которого две строки равны, равен нулю. Следствие 2. Если в определителе две строки пропорциональны, то такой определитель равен нулю. 4. Если строка определителя представлена в виде алгебраической суммы нескольких слагаемых, то определитель равен алгебраической сумме определителей, у которых в первом определителе в данной строке стоит первое слагаемое, во втором - второе слагаемое и т.д. Следствие. Если строки определителя линейно зависимы, то такой определитель равен нулю. 5. Если к элементам одной строки определителя прибавить соответствующие элементы другой, умноженные на одно и то же число, то определитель не изменится. min(m; n),называется определитель k -го порядка, полученный из матрицы А вычеркиванием (m-k) строк и (n-k) столбцов. Определение. Дополнительным минором M ij к элементу a ij квадратной матрицы An*n называется определитель (n -1) порядка, полученный из матрицы А вычеркиванием этого элемента вместе со строкой и столбцом, в которых он расположен. Определение 3. Алгебраическим дополнением A ij к элементу a ij квадратной матрицы An*n называется число A ij =
min(m; n),называется определитель k -го порядка, полученный из матрицы А вычеркиванием (m-k) строк и (n-k) столбцов. Определение. Дополнительным минором M ij к элементу a ij квадратной матрицы An*n называется определитель (n -1) порядка, полученный из матрицы А вычеркиванием этого элемента вместе со строкой и столбцом, в которых он расположен. Определение 3. Алгебраическим дополнением A ij к элементу a ij квадратной матрицы An*n называется число A ij = 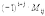 . Теорема 1. Определитель равен сумме попарных произведений элементов любой строки на их алгебраические дополнения.
. Теорема 1. Определитель равен сумме попарных произведений элементов любой строки на их алгебраические дополнения. - разложение определителя по i -й строке.
- разложение определителя по i -й строке. , взятых по одному из каждой строки и каждого столбца, причем каждое слагаемое берется со знаком "+" или "-".Определитель второго порядка. n =2, 2!=1 · 2=2 слагаемых.
, взятых по одному из каждой строки и каждого столбца, причем каждое слагаемое берется со знаком "+" или "-".Определитель второго порядка. n =2, 2!=1 · 2=2 слагаемых. . Определитель третьего порядка. n =3, 3!=1 · 2 · 3=6 слагаемых
. Определитель третьего порядка. n =3, 3!=1 · 2 · 3=6 слагаемых =
= 
 называется системой m линейных уравнений с n неизвестными, где x 1, x 2, …, x n - неизвестные, a ij, i=
называется системой m линейных уравнений с n неизвестными, где x 1, x 2, …, x n - неизвестные, a ij, i= 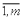 , j=
, j= 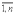 - коэффициенты при неизвестных, b 1, b 2, …, b m - свободные члены. Определение 2. Если все свободные члены равны нулю, то система называется однородной, и неоднородной - в противном случае. Oпределение 3. Решением системы называется совокупность из n чисел с 1, с 2, …, с n, при подстановке которой в систему вместо неизвестных будет получено m числовых тождеств. Определение 4. Система называется совместной, если она имеет хотя бы одно решение, и несовместной в противном случае.При изучении систем исследуют три вопроса:1) совместна система или нет;2) если система совместна, то является ли она определенной или неопределенной;3) нахождение единственного решения в случае определенной системы и всех решений в случае неопределенной.
- коэффициенты при неизвестных, b 1, b 2, …, b m - свободные члены. Определение 2. Если все свободные члены равны нулю, то система называется однородной, и неоднородной - в противном случае. Oпределение 3. Решением системы называется совокупность из n чисел с 1, с 2, …, с n, при подстановке которой в систему вместо неизвестных будет получено m числовых тождеств. Определение 4. Система называется совместной, если она имеет хотя бы одно решение, и несовместной в противном случае.При изучении систем исследуют три вопроса:1) совместна система или нет;2) если система совместна, то является ли она определенной или неопределенной;3) нахождение единственного решения в случае определенной системы и всех решений в случае неопределенной.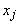 , которая войдет в число базисных, и уравнение, в котором эта переменная останется. Соответствующие столбец и строку таблицы называют ключевыми. Коэффициент
, которая войдет в число базисных, и уравнение, в котором эта переменная останется. Соответствующие столбец и строку таблицы называют ключевыми. Коэффициент  , стоящий на пересечении ключевой строки и ключевого столбца, называют ключевым.
, стоящий на пересечении ключевой строки и ключевого столбца, называют ключевым. Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.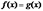 ,
, 
 .
. ,
, 
 .
.
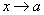 , то и алгебраическая сумма имеет предел при
, то и алгебраическая сумма имеет предел при 
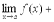
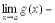
 .
.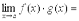

 .
.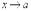 ,причем
,причем  , то и их частное имеет предел при
, то и их частное имеет предел при  ,
,  .
. .
. Теорема 2. Предел последовательности при
Теорема 2. Предел последовательности при  равен.
равен.  ,.
,.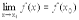 ó
ó 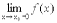 =
= 
 .
. , или
, или  Уравнение наклонной асимптоты будем искать в виде y=kx+b.
Уравнение наклонной асимптоты будем искать в виде y=kx+b.
 Если хотя бы один из пределов или не существует или равен бесконечности, то кривая у=ƒ(х) наклонной асимптоты не имеет. В частности, если k=0, то b=limƒ(х) при х →∞. Поэтому у=b -уравнение горизонтальной асимптоты.
Если хотя бы один из пределов или не существует или равен бесконечности, то кривая у=ƒ(х) наклонной асимптоты не имеет. В частности, если k=0, то b=limƒ(х) при х →∞. Поэтому у=b -уравнение горизонтальной асимптоты. R n и I
R n и I  множества D ставится в соответствие единственное число у из I, то говорят, что задана функция n переменных у=f (x 1, …, x n). Множество D называется областью определения функции D(у)=D, множество I называется множеством значений функции I (у)= I. Пример. -
множества D ставится в соответствие единственное число у из I, то говорят, что задана функция n переменных у=f (x 1, …, x n). Множество D называется областью определения функции D(у)=D, множество I называется множеством значений функции I (у)= I. Пример. - dx+
dx+  dy Для функции трех переменных u=f (x, y, z) полный дифференциал находится по формуле: du=
dy Для функции трех переменных u=f (x, y, z) полный дифференциал находится по формуле: du=  dx+
dx+  dy+
dy+  dz.
dz.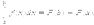
 . 2. Вычисление площади фигур, ограниченных графиками двух функций на некотором
. 2. Вычисление площади фигур, ограниченных графиками двух функций на некотором 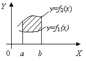 отрезке. S = S 2- S 1=
отрезке. S = S 2- S 1=  =
=  , где S 1 и S 2 - площади криволинейных трапе ций под графиками функций y=f 1(x) и y=f 2 (x). 3. Вычисление объемов тел, полученных от вращения графика функции вокруг оси ОX.
, где S 1 и S 2 - площади криволинейных трапе ций под графиками функций y=f 1(x) и y=f 2 (x). 3. Вычисление объемов тел, полученных от вращения графика функции вокруг оси ОX. 
 . 4. Вычисление объемов тел, полученных от вращения графика функции вокруг оси ОY.
. 4. Вычисление объемов тел, полученных от вращения графика функции вокруг оси ОY. , где x = f -1 (y) - обратная функция к функции y = f(x).
, где x = f -1 (y) - обратная функция к функции y = f(x). В полярных координатах
В полярных координатах 
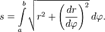



 (суммирование берется по всем элементам, на которые наше тело разбито поперечными сечениями). При переходе к пределу, когда число элементов беспредельно возрастает и наибольшее из
(суммирование берется по всем элементам, на которые наше тело разбито поперечными сечениями). При переходе к пределу, когда число элементов беспредельно возрастает и наибольшее из  , написанная сумма превращается в определенный интеграл, который дает точное значение объема V,
, написанная сумма превращается в определенный интеграл, который дает точное значение объема V,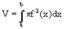

 Здесь
Здесь 
 , где
, где  — элемент площади в прямоугольных координатах.
— элемент площади в прямоугольных координатах. . Определение. Выражение вида
. Определение. Выражение вида  наз-тся числовым рядом с положительными членами. Определение. Сумма первых
наз-тся числовым рядом с положительными членами. Определение. Сумма первых  членов числового ряда называется
членов числового ряда называется  . Определение. Если существует конечный предел частичных сумм
. Определение. Если существует конечный предел частичных сумм  , то числовой ряд называется сходящимся и его сумма равна значению этого предела, иначе ряд называется расходящимся. Свойства числовых рядов: Теорема 1. Если ряд
, то числовой ряд называется сходящимся и его сумма равна значению этого предела, иначе ряд называется расходящимся. Свойства числовых рядов: Теорема 1. Если ряд  сходится и с - некоторое число, то сходится и ряд
сходится и с - некоторое число, то сходится и ряд 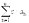 , причем выполняется равенство
, причем выполняется равенство  Теорема 2. Пусть ряды
Теорема 2. Пусть ряды 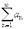 и
и  сходятся, тогда сходится ряд
сходятся, тогда сходится ряд  , причем
, причем  =
= 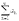 +
+  . Теорема 3. Сходимость ряда не изменится, если в нем отбросить конечное число членов.
. Теорема 3. Сходимость ряда не изменится, если в нем отбросить конечное число членов. Для системы n линейных уравнений с n неизвестными (над произвольным полем)
Для системы n линейных уравнений с n неизвестными (над произвольным полем)
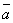 (m,n, l). Составим уравнение этой прямой.
(m,n, l). Составим уравнение этой прямой.  - каноническое уравнение прямой в пространстве.
- каноническое уравнение прямой в пространстве.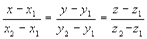 - уравнение прямой, проходящей через две данные точки.
- уравнение прямой, проходящей через две данные точки.
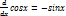








 и
и  -- две точки области, такие что весь отрезок между ними целиком лежит в R. Тогда для некоторой точки
-- две точки области, такие что весь отрезок между ними целиком лежит в R. Тогда для некоторой точки 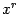 этого отрезка имеет место равенство
этого отрезка имеет место равенство




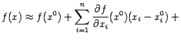
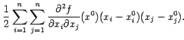
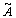 .Тогда А·А -1 =А -1 ·А=Е и А·
.Тогда А·А -1 =А -1 ·А=Е и А·  =
=  .
. 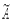 ·А·А -1 =
·А·А -1 =  . Получили противоречие.
. Получили противоречие.


