
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несобственные интегралы первого рода ⇐ ПредыдущаяСтр 7 из 7
Пусть функция y = f(x) определена и непрерывна на [ a,¥).Рассмотрим интеграл Пусть F(x) – одна Обозначим Тогда
75. Несобственные интегралы второго рода Если функция не ограничена на промежутке интегрирования и промежуток интегрирования конечен, то определенный интеграл является несобственным интегралом второго рода. 1. Пусть функция y = f(x) определена и непрерывна на [ a,b) и в точке b функция не ограничена.
Если предел, стоящий справа, существует и конечен, то несобственный интеграл называется сходящимся и равен значению этого предела, в противном случае интеграл называется расходящимся. Если F(x) первообразная функции, то Если оба предела, стоящие в правой части, существуют и конечны, то несобственный интеграл называется сходящимся и он равен сумме этих пределов, в противном случае – расходящимся. Замечание 1. Несобственные интегралы могут быть комбинированного типа: Замечание 2. Если функция на отрезке интегрирования терпит разрыв первого рода в точке с, то определенный интеграл от нее по этому отрезку не является несобственным, т.е. его можно свести к сумме двух обычных определенных интегралов. . Длина дуги кривой. Если плоская кривая задана уравнением y=f(x) её длина равна:
Если дуги пространственной кривой заданы параметрически уравнениями x= x(t), y=y(t), z= z(t) при изменении t от а до b имеем:
Вычисление площадей в прямоугольных координатах.
Отметим,что если криволинейная трапеция расположена «ниже» оси Ох (ƒ(х) < 0), то ее площадь может быть найдена по формуле
Вычисление объема тела. Пусть требуется найти объем V тела, причем известны площади S сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ох: S = S(x), а ≤ х ≤ b.
Объем тела вращения. Вычисление объема тела сводится также к вычислению определенного интеграла. Пусть рассматриваемое тело Е получается от вращения данной кривой y=f(x), заданной на сегменте [a,b], вокруг оси Ох. Обозначим через V объем данного тела. Разобьем тело поперечными сечениями, перпендикулярными к оси Ох, начиная от х=а и кончая х=b.
Очевидно поперечные сечения - круги радиуса у. Рассмотрим один из элементов Е, образованный сечениями с абсциссами х и х + х. Будем считать, что х достаточно мало и заменим объем тела Е объемом прямого цилиндра, высота которого x,а площадь основания S(x) = П f 2(x) и, следовательно, для объема V тела получим приближенное выражение
Теорема. Объем тела, получаемого при вращении вокруг оси Ох кривой y=f(x), заключенный между ординатами х=а и х=b, выражается формулой
Двойной интеграл. Двойным интегралом называют кратный интеграл с d=2.
В прямоугольных координатах:
|
||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 209; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.102.239 (0.008 с.) |
 .Вычисление несобственного интеграла можно свести к вычислению обычного определенного интеграла и нахождению предела (
.Вычисление несобственного интеграла можно свести к вычислению обычного определенного интеграла и нахождению предела (  ).
).  Если предел, стоящий справа, существует и конечен, то несобственный интеграл называется сходящимся и он равен значению этого предела. В противном случае интеграл называется расходящимся.
Если предел, стоящий справа, существует и конечен, то несобственный интеграл называется сходящимся и он равен значению этого предела. В противном случае интеграл называется расходящимся. из первообразных f(x), тогда
из первообразных f(x), тогда  .
. .
. F(¥)-F(a) - обобщенная формула Ньютона - Лейбница (для вычисления несобственного интеграла).
F(¥)-F(a) - обобщенная формула Ньютона - Лейбница (для вычисления несобственного интеграла). .
. 2.Пусть функция y = f(x) определена и непрерывна на [ a,c)È(c,b ], и в точке с функция терпит разрыв второго рода.
2.Пусть функция y = f(x) определена и непрерывна на [ a,c)È(c,b ], и в точке с функция терпит разрыв второго рода.  .
. первого и второго рода; или второго рода с несколькими точками разрыва второго рода.
первого и второго рода; или второго рода с несколькими точками разрыва второго рода.
 В полярных координатах
В полярных координатах 
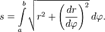


 или
или 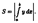 Площадь фигуры, ограниченной кривыми у = = fι(x) и у = ƒг(х), прямыми х = а и х = b (при условии ƒ2(х) ≥ ƒ1(х)) можно найти по формуле
Площадь фигуры, ограниченной кривыми у = = fι(x) и у = ƒг(х), прямыми х = а и х = b (при условии ƒ2(х) ≥ ƒ1(х)) можно найти по формуле 


 (суммирование берется по всем элементам, на которые наше тело разбито поперечными сечениями). При переходе к пределу, когда число элементов беспредельно возрастает и наибольшее из
(суммирование берется по всем элементам, на которые наше тело разбито поперечными сечениями). При переходе к пределу, когда число элементов беспредельно возрастает и наибольшее из  , написанная сумма превращается в определенный интеграл, который дает точное значение объема V,
, написанная сумма превращается в определенный интеграл, который дает точное значение объема V,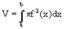

 Здесь
Здесь 
 , где
, где  — элемент площади в прямоугольных координатах.
— элемент площади в прямоугольных координатах.


