
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамика несвободной системы с двумя степенями свободы ⇐ ПредыдущаяСтр 8 из 8
Для изучения движения механических систем со связями, каковыми являются приведенные в расчетной работе №2 динамические модели, используются дифференциальные уравнения движения в обобщенных координатах (уравнения Лагранжа второго рода). Рассмотренные примеры выполнения расчетной работы №2 указывают на особенность расчетно-теоретического исследования практических задач. В частности, объем работ на этапе формулировки задачи и вывода основных уравнений, описывающих рассматриваемые движения системы, может значительно превосходить объем работ по решению полученных уравнений на ПК. На приведенных задачах полезно отрабатывать навыки составления (правильность выбора обобщенных координат, представления кинетической энергии системы и виртуальной работы, определения обобщенных сил, вычисления производных кинетической энергии, составляющих левую часть уравнений Лагранжа); решения задач (выбор алгоритма решения задачи и его реализация на ПК); исследования полученных результатов и влияния параметров системы на ее движение. Схемы конструкций и исходные данные Схемы конструкций представлены на рис. 5.1, исходные данные – в табл.5.1. Последняя цифра зачетной книжки (шифр) является основанием для выбора варианта задачи. По последней цифре шифра (ПЦШ) выбирается номер схемы и номер условий в соответствующей таблице. Конкретно задача сформулирована в соответствии с номером рисунка схемы.
Рис. 5.1. Схемы конструкций к расчетной работе №2 Т а б л и ц а 5.1
Здесь Вариант 0. Ползун 1 массой m 1 может скользить без трения по горизонтальной направляющей. К ползуну подвешен математический маятник 2 длиной l имассой m 2. Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ. Вариант 1. Призма 1, имеющая массу m 1, скользит по гладкой горизонтальной плоскости, удерживаемая горизонтальной пружиной жесткостью С 1. По наклонной грани призмы катится без скольжения однородный цилиндр 2, имеющий массу m 2. К его центру под углом Y к горизонту приложена сила У к а з а н и я. 1. Обобщенная координата 2. При задании величин F, m 2, a следует соблюдать условие Вариант 2. Ползун 1 прикрепленный к основанию горизонтальной пружиной жесткостью С 1 массой m 1 скользит без трения по горизонтальной направляющей. К ползуну подвешен математический маятник 2 длиной l имассой m 2, к точке B маятникаприложена постоянная по величине сила
У к а з а н и е. Обобщенная координата Вариант 3. Призма 1, имеющая массу m 1, скользит по наклонной плоскости без трения. По наклонной грани призмы катится без скольжения однородный цилиндр 2, массой m 2, центр которого прикреплен к призме пружиной жесткостью С 1. К центру диска 2 под углом Y к горизонту приложена сила
У к а з а н и я. 1. Обобщенная координата 2. При задании величин F, m 2, a следует соблюдать условие Вариант 4. Ползун 1 массой m 1 скользит без трения по горизонтальной направляющей. К ползуну подвешен математический маятник 2 длиной l имассой m 2, связанный с ползуном спиральной пружиной с крутильной жесткостью С j. При нижнем положении маятника пружина не деформирована. К точке B маятникаприложена постоянная по величине сила Вариант 5. Груз 1 массой m 1 и пренебрежимо малых размеров может скользить без трения по стержню 2 достаточно большой длины l 2имассой m 2, будучи удерживаемым пружиной жесткостью С1. Длина недеформированной пружины l. К грузуприложена постоянная по величине сила
Вариант 6. Доска 1 массой m 1может передвигаться на роликах 3, 4 с массой m 3 = m 4 , катящихся без скольжения по горизонтальной плоскости. По доске 1 катится без скольжения цилиндр 2 массой m 2. Доска удерживается горизонтальной пружиной жесткостью С 1. К оси цилиндраприложена постоянная по величине сила У к а з а н и я. 1. Обобщенная координата 2. При задании величин F, m 2 следует соблюдать условие Вариант 7. Тележка 1 массой m 1, имеющая два колеса 3, 4 массой m 3 = m 4 , может катиться без сопротивления по горизонтальной плоскости. При этом колеса катятся без скольжения. По тележке 1 катится без скольжения однородный диск 2 массой m 2, центр которого соединен с тележкой горизонтальной пружиной жесткостью С 1. К центру диска 2 приложена постоянная по величине сила У к а з а н и я. 1. Обобщенная координата 2.При задании величин F, m 2следует соблюдать условие Вариант 8. Тележка 1 массой m 1, имеющая два колеса 3, 4 массой m 3 = m 4 , может катиться без сопротивления по горизонтальной плоскости. При этом колеса катятся без скольжения. По тележке 1 катится без скольжения однородный диск 2 массой m 2, центр которого соединен с неподвижным основанием горизонтальной пружиной жесткостью С 1. К центру диска 2 приложена постоянная по величине сила
У к а з а н и я. 1. Обобщенная координата 2. При задании величин F, m 2следует соблюдать условие Вариант 9. Груз 1 массой m 1 и пренебрежимо малых размеров может скользить без трения по стержню 2 достаточно большой длины l 2имассой m 2. Стержень удерживается спиральной пружиной с крутильной жесткостью С j. В нижнем положении стержня пружина не деформирована. К грузуприложена постоянная по величине сила
Пример. Дано. Центры однородных дисков (рис. 5.2), способных катиться по горизонтальной плоскости без скольжения, связаны пружиной, коэффициент жесткости которой равен C. Массы дисков m 1 и m 2. К диску 1 приложен момент сил сопротивления качению M 1 Z = –
Рис. 5.2
В соответствии с разд. 2 составим дифференциальные уравнения, описывающие движение системы (рис. 5.2). 1. Выберем обобщенные координаты. Для этого введем горизонтальные оси O 1 X 1 и O 2 X 2, неизменно связанные с плоскостью, по которой катятся диски. Начала отсчета O 1 и O 2 на этих осях выберем так, чтобы расстояние O 1 O 2 равнялось длине недеформируемой пружины. В качестве обобщенных координат выберем координату центра A диска 1 на оси OX 1 и координату центра B диска 2 на оси OX 2: q 1 = x 1 A, q 2 = x 2 B. 2. Представим кинетическую энергию системы в виде
3. Определим обобщенные силы. Для этого рассмотрим систему сил, приложенных к системе материальных точек, состоящую из сил, не зависящих от ограничивающих тел и сил трения. В эту систему войдут сила F–, силы тяжести P– 1 и P– 2, реакции пружины R– 1, R– 2, моменты сил сопротивления M– 1и M– 2. Введем в рассмотрение оси AZ 1 и BZ 2(рис. 5.2). Алгебраические величины указанных сил и моментов на соответствующих осях могут быть записаны в виде
При записи выражений для сил реакций пружины учтем, что из-за выбора обобщенных координат разница между текущей длиной пружины l и длиной недеформированной пружины l 0 равна разности координат центров дисков: l – l 0 = x 2 B + l 0 – x 1 A – l 0 = x 2 B – x 1 A, поэтому
Рассмотрим виртуальное перемещение системы, при котором обобщенная координата q 1 = x 1 A получает приращение δ q 1 = δ x 1 A, а обобщенная координата q 2 = x 2 B не меняется. Сосчитаем виртуальную работу: δ Aq 1 = R 1 X 1 δ x 1 A + M 1 Z δφ1, где
Отсюда с учетом (5.3), (5.4) получим выражение для первой обобщенной силы:
Рассмотрим виртуальное перемещение системы, при котором обобщенная координата q 1 = x 1 A не меняется, а q 2 = x 2 B получает приращение δ q 2 = δ x 2 B. Аналогично (5.3) … (5.5) сосчитаем виртуальную работу и получим выражение для обобщенной силы:
4. Дифференцируя выражение для кинетической энергии (5.1), составим уравнения Лагранжа II рода:
или
Курсовая работа
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 195; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.185.123 (0.028 с.) |

 , м/c
, м/c
 - массы;
- массы;  - линейная жесткость пружины;
- линейная жесткость пружины;  - крутильная жесткость пружины; l, l2 - длины; R - радиус; F - сила;
- крутильная жесткость пружины; l, l2 - длины; R - радиус; F - сила; 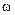 - частота, с-1;
- частота, с-1;  - коэффициент сопротивления качению;
- коэффициент сопротивления качению;  - угол, рад;
- угол, рад;  , все
, все  = 0 с-1, мс-1 - рекомендуемые значения начальных условий обобщенных координат и скоростей.
= 0 с-1, мс-1 - рекомендуемые значения начальных условий обобщенных координат и скоростей. , величина которой постоянна. Угол Y линейно меняется со временем:
, величина которой постоянна. Угол Y линейно меняется со временем:  . Угол наклона призмы к горизонту a. Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ.
. Угол наклона призмы к горизонту a. Составить дифференциальные уравнения движения системы и рассчитать конкретное движение на ЭВМ. отсчитывается от положения призмы, при котором пружина не деформирована.
отсчитывается от положения призмы, при котором пружина не деформирована. , кг.
, кг. отсчитывается от положения центра диска, при котором пружина не деформирована.
отсчитывается от положения центра диска, при котором пружина не деформирована. , кг.
, кг. .
. ω1 Z, а к диску 2M 2 Z = –
ω1 Z, а к диску 2M 2 Z = –  ω2 Z, пропорциональные соответствующим угловым скоростям. К центру диска 2 приложена постоянная по величине сила
ω2 Z, пропорциональные соответствующим угловым скоростям. К центру диска 2 приложена постоянная по величине сила 
 ). Она складывается из кинетических энергий дисков, каждый из которых совершает плоскопараллельное движение. При этом T = T 1 + T 2, где
). Она складывается из кинетических энергий дисков, каждый из которых совершает плоскопараллельное движение. При этом T = T 1 + T 2, где  ,
,  . В итоге, переходя к обозначениям
. В итоге, переходя к обозначениям 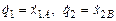 , получаем
, получаем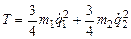 . (5.1)
. (5.1) (5.2)
(5.2)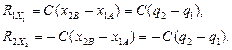 (5.3)
(5.3) – приращение угла поворота, соответствующее приращению δ x 1 A координаты центра диска 1, тогда
– приращение угла поворота, соответствующее приращению δ x 1 A координаты центра диска 1, тогда . (5.4)
. (5.4) . (5.5)
. (5.5)
 (5.6)
(5.6)



