
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Возможные и виртуальные перемещения
Перемещение материальной точки зависит от ее массы, приложенных к точке сил связей и начальных условий. Определение перемещения точки сводится к решению задачи динамики точки. В аналитической механике используются два основных понятия о возможном и виртуальном перемещениях точки. Пусть на материальную точку наложена голономная нестационарная удерживающая связь, уравнение которой
Возможнымперемещением несвободной материальной точки называется такое бесконечно малое перемещение, отвечающее бесконечно малому промежутку времениdt, которое допускается наложенными на систему ограничениями – связями,
Рис. 2.5
Раскладывая функцию (2.5) в ряд Тейлора с точностью до слагаемых выше первого порядка малости и учитывая, что связь имеет вид (2.4), получаем
Выражение (2.6) представляет собой условие, которому должны удовлетворять проекции вектора d Виртуальнымперемещением несвободной материальной точки, отвечающим данному моменту времени t, называется такое воображаемое, бесконечно малое, прямолинейное, соответствующее данному моменту времени t перемещение точки, которое могло бы иметь место, если начиная с этого момента времени связи, наложенные на ее движение, сделались бы неизменяемыми. Виртуальныеперемещения точки обозначаются вариациями: вектор Виртуальныеперемещения не связаны ни с движением точки, ни с изменением наложенных связей. Они представляют собой воображаемые перемещения, которые можно представить совокупностью бесконечно малых векторов
Пример 2.5. Представим теперь (см. рис. 2.5), что перемещение точки из положения, занимаемого ею в данный момент времени, в бесконечно близкое происходит в результате изменения координат точки при фиксированном времени t (т.е. либо вертикально вверх (р =4), либо вертикально вниз (р =1), функция (парабола y = p x 2, p= 2 ) как бы изменяется не за счет аргумента, а за счет параметра р). Координаты точки с учетом их вариации должны удовлетворять уравнению связи
Раскладывая эту функцию в ряд Тейлора с точностью до слагаемых выше первого порядка малости и учитывая, что связь имеет вид (2.4), получаем
Таким образом, при наличии связи вида (2.4) вариации координат точки должны удовлетворять условию (2.8), при выводе которого время полагалось фиксированным. Поэтому данное условие должно выполняться как при стационарных, так и при нестационарных связях, наложенных на точку. Используя понятие вектора-градиента, выражение (2.8) можно рассматривать как скалярное произведение векторов
и
Вектор-градиент расположен вдоль главной нормали к поверхности Так как по определению, виртуальным перемещением несвободной точки, отвечающим фиксированному моменту времени t, называется такое воображаемое, бесконечно малое, прямолинейное, соответствующее данному моменту времени перемещение точки, которое могло бы иметь место, если начиная с этого момента времени связи, наложенные на ее движение, сделались бы неизменяемыми, то в данном случае точка М может переместиться только вертикально либо вверх в положение М в, либо вниз – в положение М н. Это значит, что изменение функции в данный момент времени t произошло не за счет аргумента x, а за счет параметра p, пусть p =4 или p =1. Это и будет виртуальным перемещением точки d y, отвечающим функции y = p·x 2 (рис. 2.5), где p =2.
В дальнейшем условимся применять краткое выражение: С точки зрения математики, виртуальные перемещения – это изохронные вариации координат точек, подчиненные уравнениям связи. Так как слово «перемещение» ассоциируется с «передвижением», то, может быть, для понимания существа метода вместо термина «виртуальные перемещения» следует употреблять термин «изохронные вариации» - ведь когда мы сообщаем виртуальное перемещение, в действительности никакого передвижения не происходит. Поэтому криволинейные перемещения точек заменяют прямолинейными отрезками, отложенными по касательным к траекториям точек. Установим связь между элементарными возможными и виртуальными перемещениями точек. Если наложенная на точку связь стационарная, то При нестационарной связи условие (2.6) для проекций вектора d Пример 2.6. Математический маятник (рис. 2.3). Точка О – цилиндрический шарнир, ОМ= l – невесомый нерастяжимый стержень. Уравнения связей удерживающих (двусторонних), голономных стационарных: 1) z = 0, 2) x 2 + y 2 – l 2 = 0. Координаты точки М: x = l cos (j), y = l sin (j). Их вариации d x = - l sin (j) dj, d y = l cos (j) dj. Виртуальное перемещение Пример 2.7. Если ОМ = l (t), (рис. 2.4), то уравнения связей будут иметь вид: 1) z = 0, 2) x 2 + y 2 – l (t) 2 £ 0. Связи неудерживающие (односторонние), голономные, нестационарные. Координаты точки М: x = l (t) cos (j), y = l (t) sin (j). Их вариации 2.4. Обобщенные координаты. Число степеней свободы Пусть механическая система состоит из n материальных точек. Положение такой системы в пространстве определяется 3 n декартовыми координатами, так как максимальное число степеней свободы для точки в пространстве s = 3. Если на систему наложено h голономных удерживающих связей, то независимыми между собой будут не 3 n, а s = 3 n – h вариаций координат, а остальные h зависимые. Число независимых координат – число независимых виртуальных перемещений – называется числом степеней свободы системы. Выбрав s = 3 n – h декартовых координат системы в качестве независимых, остальные h координат можно найти при помощи уравнений связей. Выбор декартовых координат в качестве независимых для ряда задач механики оказывается нерациональным, так как приводит к громоздким выкладкам. Поэтому целесообразно использовать и другие независимые координаты.
Обобщенными (лагранжевыми) координатами называются независимые между собой параметры, которые однозначно определяют положение несвободной механической системы в пространстве в любой момент времени; обозначаются qi (t), где
Остальные декартовы координаты выражаются через те же обобщенные координаты с помощью h уравнений связей. Таким образом, обобщенные координаты q 1, q 2, …, qi, …, qs обладают следующими свойствами: · вещественны, т.е. не могут принимать комплексных значений; · не зависимы друг от друга; · имеют самостоятельный геометрический смысл. Это значит, что эти переменные определяют положение системы, т.е. значения декартовых координат ее точек до написания (и тем более до интегрирования) уравнений движения. Производные от обобщенных координат по времени На практике при выборе обобщенных координат qi, как правило, нет необходимости в выписывании явных выражений для функций qk (t, Xj). Например, если точка находится на поверхности сферы с радиусом r = r (t), то в качестве обобщенных координат qi (i = 1,2,3) можно принять углы Эйлера: y – угол прецессии, q – угол нутации, j – угол ротации (или собственного вращения) сферической системы координат. Обобщенные координаты могут быть выбраны удачно, поэтому решение конкретной задачи может быть проще и нагляднее. В иных случаях выбор координат qi не будет таким удачным. Общего правила, как выбирать обобщенные координаты, не существует. Можно высказать лишь некоторые наводящие соображения, связанные со структурой системы и с характером силовых полей. Главное здесь – это личный опыт, приобретаемый при решении задач. В качестве обобщенных координат могут приниматься не только линейные (отрезки прямых), но и угловые (дуги, углы) перемещения, а также любые другие параметры, удовлетворяющие определению обобщенных координат. Отметим, что для одной и той же механической системы может быть несколько вариантов обобщенных координат. Конкретный их выбор определяется поставленной задачей. Дальнейшая теория излагается для неизменяемой системы с голономными нестационарными удерживающими связями (2.1). Механическая система, расстояние между точками которой в процессе ее движения не изменяется, называется неизменяемой.
Пример 2.8. Все декартовы координаты точек выразить через обобщенные координаты. Так, положение кривошипно-ползун-ного механизма, показанного на рис. 2.6, определяется двумя точками А и В. Из четырех декартовых координат (xА, yА, xВ, yВ) независимой будет только одна, так как число h голономных удерживающих связей равно трем (h = 3): длина кривошипа
Рис. 2.6 Если за независимую декартову координату принять xА,а за обобщенную - угол j(q = j) поворота кривошипа 1 против часовой стрелки, то xА= l 1·cosj. Другие декартовы координаты Таким образом, все декартовы координаты точек системы выражены через угол j, принятый за обобщенную координату q = j. Пример 2.9. Выразить виртуальные перемещения точек А и В стержня (рис. 2.7) через его обобщенную координату.
Число степеней свободы s = 1, и в качестве обобщенной координаты можно выбрать угол Примеры определения числа степеней свободы в различных случаях: 1. Система, состоящая из двух материальных точек, соединенных между собой стержнем, имеет пять степеней свободы. Как известно, положение двух точек определяется шестью координатами (x 1, y 1, z 1), (x 2, y 2, z 2), между которыми существует одно соотношение – уравнение связи (x 1 - x 2)2 + (y 1 - y 2 )2 + (z 1 - z 2)2 = L 2, выражающее условие постоянства квадрата расстояния между ними. Следовательно, здесь n = 2, h = 1 и число степеней свободы s = 3 n – h = 3 × 2 – 1 = 5. 2. Для материальной точки, движущейся по поверхности, 3. Свободное твердое тело имеет шесть степеней свободы, ибо оно обладает независимыми друг от друга возможными поступательными перемещениями по трем взаимно перпендикулярным осям и тремя независимыми друг от друга возможными поворотами вокруг трех взаимно перпендикулярных осей. Любой другой вид движения твердого тела можно рассматривать как частный случай. Большего числа степеней свободы твердое тело как самостоятельный объект изучения никогда не имеет. 4. Твердое тело, имеющее одну закрепленную точку, обладает тремя степенями свободы.
5. Твердое тело с двумя неподвижными точками имеет одно возможное перемещение – поворот вокруг оси, проходящей через эти точки, т.е. одну степень свободы.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 663; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.186.164 (0.041 с.) |
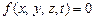 . (2.4)
. (2.4) (dx, dy, dz)(рис. 2.5). Этому уравнению удовлетворяют координаты точки М в момент времени t. Через
(dx, dy, dz)(рис. 2.5). Этому уравнению удовлетворяют координаты точки М в момент времени t. Через  точки также должны удовлетворять уравнению связи:
точки также должны удовлетворять уравнению связи: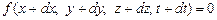 . (2.5)
. (2.5)
 . (2.6)
. (2.6) называют вариацией радиуса-вектора точки,а проекции на оси декартовой системы координат - вариациями координат d x,d y,d z.
называют вариацией радиуса-вектора точки,а проекции на оси декартовой системы координат - вариациями координат d x,d y,d z. и виртуальным
и виртуальным  . (2.7)
. (2.7) . (2.8)
. (2.8) :
:
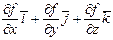 (2.9)
(2.9) . (2.10)
. (2.10) Поэтому условие (2.8) означает что вектор
Поэтому условие (2.8) означает что вектор  ортогонален главной нормали и, следовательно, расположен по касательной. Поэтому при исследовании несвободного движения точки, системы точек или системы тел удобно пользоваться образом касательного пространства. В качестве примера рассмотрим движение материальной точки по гладкой плоской кривой, пусть это будет уравнение параболы y = p x 2 (рис. 2.5), где p =2. Положение материальной точки М определяется ее координатами (x, y). Однако y = ƒ (x) и, следовательно, положение точки М полностью задается только величиной x. Пусть за промежуток времени dt точка М переместится и займет положение М' с координатами (x+dx), (y+dy).
ортогонален главной нормали и, следовательно, расположен по касательной. Поэтому при исследовании несвободного движения точки, системы точек или системы тел удобно пользоваться образом касательного пространства. В качестве примера рассмотрим движение материальной точки по гладкой плоской кривой, пусть это будет уравнение параболы y = p x 2 (рис. 2.5), где p =2. Положение материальной точки М определяется ее координатами (x, y). Однако y = ƒ (x) и, следовательно, положение точки М полностью задается только величиной x. Пусть за промежуток времени dt точка М переместится и займет положение М' с координатами (x+dx), (y+dy). и условие (2.6) аналогично условию (2.8). Следовательно, если связь стационарная, то элементарное возможное перемещение точки совпадает с одним из виртуальных.
и условие (2.6) аналогично условию (2.8). Следовательно, если связь стационарная, то элементарное возможное перемещение точки совпадает с одним из виртуальных. . (2.11)
. (2.11) называются обобщенными скоростями.
называются обобщенными скоростями.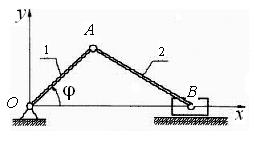
 Решение. Положение стержня в плоскости xOy определяется четырьмя декартовыми координатами точек А и В. Уравне-
Решение. Положение стержня в плоскости xOy определяется четырьмя декартовыми координатами точек А и В. Уравне- . Так как xА = l cosj, то
. Так как xА = l cosj, то  . Аналогично радиус-вектор точки В равен
. Аналогично радиус-вектор точки В равен  , так как yВ = l sinj, то
, так как yВ = l sinj, то 



