
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ж. Н. Андреева, О. Г. Агошков, А. В. БеловСодержание книги
Поиск на нашем сайте Ж.Н. АНДРЕЕВА, О.Г. АГОШКОВ, А.В. БЕЛОВ
ДИНАМИКА КОНСТРУКЦИЙ ВОЕННО-ТЕХНИЧЕСКИХ КОМПЛЕКСОВ
Министерство образования и науки Российской Федерации Балтийский государственный технический университет «Военмех»
Ж.Н. АНДРЕЕВА, О.Г. АГОШКОВ, А.В. БЕЛОВ
ДИНАМИКА КОНСТРУКЦИЙ ВОЕННО-ТЕХНИЧЕСКИХ КОМПЛЕКСОВ
Учебное пособие
Санкт-Петербург УДК 531.36: 623.1/.3(075.8)
А65 УДК 531.36: 623.1/.3(075.8)
Р е ц е н з е н т ы: канд. техн. наук, доц. Е.В. Погудин;
Утверждено редакционно-издательским советом университета
ISBN 5-85546-187-4 © БГТУ, 2006 © Авторы, 2006
Введение
Развитие артиллерийского, стрелково-пушечного и ракетного вооружения с точки зрения динамического воздействия можно охарактеризовать ростом удельных нагрузок в несущих элементах конструкции, обусловленным снижением габаритов и веса проектируемых установок и одновременным повышением их баллистических характеристик. Подобные виброударные воздействия существенно влияют на такие свойства конструкции, как металлоемкость, эффективность, устойчивость, прочность, эргономичность, точность и др. Поэтому необходимо изучать теорию и практику проектирования и экспериментальной отработки указанных образцов вооружения как динамических объектов, при этом существенное влияние оказывают вид носителя и его особенности. Постоянное ужесточение требований по материалоемкости конструкции и расширяющиеся эксплуатационные условия при возрастающей энергонапряженности конструкции делают эту проблему все более актуальной. Главная задача в изучении данной дисциплины состоит в том, чтобы будущий специалист был знаком: – с прикладными возможностями динамического анализа конструкций образцов вооружения; – с существующими программными продуктами для решения динамических задач на ПЭВМ; – а также с экспериментальными методами регистрации динамических процессов. Данная дисциплина в системе подготовки является одной из завершающих, поэтому предполагается, что физические процессы, протекающие в подсистемах конструкций образцов вооружения, студентам известны. Основные разделы дисциплины содержат накопленные в отрасли научно-технические и методические материалы. Использован также опыт смежных отраслей машиностроения. В результате изучения дисциплины студенты должны: – сформировать практические навыки по динамическому анализу конструкций образцов вооружения различных компоновочных схем; – углубить знания по спектральному составу возмущающих факторов, воздействующих на артиллерийское орудие как при движении носителя (например, возмущений от качки корабля), так и при выстреле, а также при различных условиях ведения стрельбы (например, из неподвижного орудия или с ходу, одиночными выстрелами или очередями и т.д.); – уметь корректно ставить задачу, создавать соответствующие математические динамические модели, отражающие процессы нагружения основных элементов конструкции; – уметь составлять алгоритмы проектировочных динамических расчетов с использованием современных программных продуктов и уметь их применять на ПЭВМ; – иметь представление об основных экспериментальных методах исследования, используемых в сложных динамических расчетах; – уметь проводить математические исследования на ПЭВМ, чтобы составить полную картину о динамике конструкции, действующих на нее нагрузках и т.д. Связи и их классификация 1. Связи называются голономными, если они описываются уравнениями вида
Такие связи накладывают ограничения на координаты точек, а значит, на положение системы в пространстве. Это так называемые геометрические связи. Вместе с тем, голономные связи накладывают ограничения и на скорости точек системы. Соответствующие условия получаются в результате дифференцирования уравнений (2.1) по времени:
Голономные связи могут описываться и дифференциальными уравнениями, однако последние обязательно должны быть интегрируемыми. Пример 2.1. Получить уравнения связей для диска радиусом r, который катится без скольжения по плоскости (рис. 2.1).
Неголономными называются связи, которые описываются уравнениями вида
Уравнения (2.3), в отличие от уравнений голономных связей, не могут быть проинтегрированы независимо от дифференциальных уравнений движения системы. Неголономные связи накладывают ограничения (2.3) на скорости точек, поэтому их называют кинематическими. Пример 2.2. Получить уравнения связей для шара радиусом r, который катится без скольжения по плоскости (рис. 2.2).
Рис. 2.2 Решение. Положение шара определяется координатами xc, yc, zc центра масс и тремя углами его поворота вокруг центра масс. Этими углами могут быть углы Эйлера. При любом положении шара расстояние от точки С до плоскости Оxy равно его радиусу. Поэтому одно из уравнений связи имеет вид zc = r. Другие уравнения связи определяются из условия качения без скольжения: Проецируя это векторное уравнение на оси неподвижной системы координат, получаем Кинематические уравнения в проекциях на оси неподвижной системы координат имеют вид
Таким образом, уравнениями связей для шара являются Первые два из них не интегрируются, т.е. являются уравнениями неголономных связей. 2. Связи подразделяются на стационарные и нестационарные в зависимости от того, входит в явном виде время в уравнение связи или нет. Связь, уравнение которой имеет вид
3. Связи называют удерживающими (двусторонними), если они являют- В этом случае говорят, что точка в любой момент времени остается на связи. Неудерживающая (односторонняя) связь описывается неравенством нулю. Например, если математический маятник представляет собой тонкий стержень длиной l, вращающийся вокруг неподвижной оси, к свободному концу которого прикреплен груз (материальная точка), то связь для груза будет удерживающей. Е сли же груз прикреплен к свободному концу нерастяжимой нитью длиной l (t),то связь будет неудерживающей, поскольку груз может находиться как на поверхности сферы радиусом l (t), так и внутри ее x 2 + y 2- l 2(t)£ 0. Обобщенные силы В аналитической механике, наряду с понятием о силе как векторной величине, характеризующей воздействие на данное тело других материальных тел, используют понятие об обобщенной силе. Для определения обобщенной силы рассмотрим виртуальную работу сил, приложенных к точкам системы,
Если механическая система при наложенных на нее голономных удерживающих h связях имеет s = 3 n - h степеней свободы, то ее положение определяется обобщенными координатами
Подставляя
Скалярную величину
называют обобщенной силой, соответствующей i -й обобщенной координате. Подставляя (2.14) в (2.13), получаем формулу для виртуальной работы
Обобщенной силой, соответствующей i - й обобщенной координате, называется множитель при вариации данной обобщенной координаты в выражении виртуальной работы сил, действующих на механическую систему. Виртуальная работа определяется от задаваемых активных сил, независящих от ограничений, и реакций связей (если связи не идеальны, то для решения задачи необходимо дополнительно задать физическую зависимость Tj от Nj (Tj – это, как правило, силы трения или моменты сопротивления трению качения, которые мы умеем определять). В общем случае обобщенная силаявляется функцией обобщенных координат, скоростей точек системы и времени. Из формулировки следует, что обобщенная сила – скалярная величина, которая зависит от выбранных для данной механической системы обобщенных координат. Это значит, что при изменении набора обобщенных координат, определяющих положение данной системы, изменятся и обобщенные силы. Пример 2.10. Для диска радиусом r и массой m, который катится без скольжения по наклонной плоскости (рис. 2.9), за обобщенную координату можно принять: либо q = s - перемещение центра масс диска, либо q = j - угол поворота диска. Если пренебречь сопротивлением качению, то в первом случае обобщенной силой будет Qs = mg sina, а во втором - Q j = mg r sina.
Существуют различные способы вычисления обобщенных сил. 1. Согласно (2.14), обобщенная сила
Принимая во внимание, что
Этот способ определения обобщенных сил называют аналитическим. Пример 2.11. Найти обобщенную силу Qq= j, если в кривошипно-ползунном механизме (рис. 2.10) OA=AB= l, Решение. Так как F 1 x= 0и F 2 y= 0, то обобщенная сила согласно (2.16)
Проекции сил и координаты точек их приложения определяются как F 1 y=- F 1; F 2 x=- F 2; yA = l sinj; xB = 2 l cosj. Следовательно, Qq= j= - F 1 l cosj + 2 F 2 l sinj.
Рис. 2.10
2. Укажем на более простой способ вычисления обобщенной силы. Обобщенные силы для механических систем с числом степеней свободы s=k > 1целесообразно вычислять последовательно, учитывая, что обобщенные координаты, а значит, и их вариации тоже не зависят друг от друга. Системе всегда можно сообщить такое виртуальное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не варьируются. В этом случае из (2.15) получаем
Индекс qi в (2.17) означает, что виртуальная работа сил, действующих на систему, определяется на перемещениях точек приложения этих сил, соответствующих вариации только одной i- йобобщенной координаты. Пример 2.12. Найти обобщенные силы Решение. Для определе-ния обобщенной силы
где P 1 =m 1 g; P 2 =m 2 g. Определяя
3. Если силы, действующие на механическую систему, потенциальные, то для определения обобщенных силможно использовать силовую функцию U или потенциальную энергию П системы. Потенциальная сила
Подставляя проекции силы Так как U = - П,то
Пример 2.13. В системе, показанной на рис. 2.12, массы груза 1 и цилиндра 2 равны m 1и m 2соответственно, радиус цилиндра r, а коэффициент жесткости пружины с 1 .
Рис. 2.12
Полагая, что трение между грузом и наклонной плоскостью отсутствует, а траектория точки С – центра масс цилиндра – вертикаль, найти обобщенные силы Решение. Потенциальная энергия системы
Обобщенные силы, соответствующие обобщенным координатам:
2.7. Уравнения Лагранжа II рода (без вывода) Уравнения Лагранжа второго рода представляют собой дифференциальные уравнения движения несвободной механической системы, составленные в обобщенных координатах. Рассматривается движение системы, состоящей из n материальных точек относительно инерциальной системы отсчета. Наложенные на систему h связей – голономные, удерживающие, нестационарные. Если связи неидеальные, то соответствующие им реакции следует добавить к действующим на систему активным силам. Пусть система имеет s = 3 n – h степеней свободы и ее положение определяется q 1, q 2, …, qi, …, qs обобщенными координатами, а радиус-вектор любой точки этой системы - формулой (2.11): Виртуальноеперемещение k -й точки
Уравнения Лагранжа второго рода формулируются следующим образом:
где T – кинетическаяэнергия механической системы; число уравнений Лагранжа II рода равно i = s числу степеней свободы системы; т.е. полная производная по времени d/dt от частной производной от кинетической энергии системы по обобщенной скорости В уравнения Лагранжа не входят заранее неизвестные реакции идеальных связей. Если силы, действующие на систему, потенциальные, то обобщенные силы находятся по формуле (2.18), а уравнения Лагранжа второго рода в этом случае преобразуются к виду
Функция, равная разности кинетической и потенциальных энергий механической системы, называется функцией Лагранжа L = T – П. Так как потенциальная энергия системы является функцией только обобщенных координат, то
При использовании функции Лагранжа уравнения(2.21) принимают вид
Кинетическая энергия механической системы, состоящей из n материальных точек, как известно, определяется по формуле
Принимая во внимание выражение (2.19), кинетическую энергию системы можно записать в виде
где
Если наложенные на систему связи стационарные, то
Производные от кинетической энергии (2.25) по обобщенной скорости
Так как
Подставляя эти выражения в уравнение Лагранжа (2.20), получаем
Так как обобщенные силы - функции обобщенных координат, времени и, возможно, обобщенных скоростей, то каждое из уравнений (2.26) имеет второй порядок. Порядок уравнений не изменится и при нестационарных связях, так как в этом случае в выражения (2.26) войдут слагаемые, зависящие только от обобщенных координат, обобщенных скоростей и времени. Таким образом, уравнения Лагранжа второго рода для механической системы с голономными связями представляют собой систему обыкновенных дифференциальных уравнений порядка 2 n относительно обобщенных координат. Уравнения Лагранжа второго рода сыграли решающую роль в развитии динамики систем и широко используются для решения многих задач динамики многопараметрических систем. Следует отметить, что для понимания существа и особенностей метода Лагранжа недостаточно изучения одной теории, необходимо рассматривать много примеров и задач. Изучение уравнений Лагранжа должно быть предметным. 2.8. Последовательность действий при использовании
1.Определить число степеней свободы системы и выбрать наиболее удобные обобщенные координаты. 2. Вычислить кинетическую энергию системы в ее абсолютном движении и выразить эту энергию через обобщенные координаты Напомним формулы кинетических энергий в абсолютном движении: · для материальной точки · длясистемы материальных точек · длятвердого тела: – при поступательном движении – при вращении вокруг неподвижной оси l – при плоскопараллельном движении
– при вращении вокруг неподвижной точки – в общем случае движения твердого тела
3. Вычислить производные от кинетической энергии, входящие в левую часть уравнений Лагранжа. 4. Определить обобщенные силы, соответствующие выбранным обобщенным координатам (так как каждой обобщенной координате соответствует обобщенная сила, то число обобщенных сил механической системы равно числу обобщенных координат, причем размерность каждой из обобщенных сил соответствует размерности соответствующей обобщенной координаты). 5. Подставить все вычисленные величины в уравнения Лагранжа. Пример 2.14. Механическая система (рис. 2.13) состоит из однородного круглого цилиндра 1 массой m 1 и радиусом r, однородного стержня 2 длиной l и массой m 2, к которому в точках А и В шарнирно прикреплены ползуны 3 и 4 массами m 3и m 4, а также двух пружин с коэффициентами жесткости С 1 и С 2. Цилиндр без скольжения катится по горизонтальной плоскости. К нему приложена пара сил с моментом М 1(t). Пренебрегая сопротивлением качению цилиндра 1, трением в шарнирах и направляющих, а также массой пружин, составить дифференциальные уравнения движения системы.
Рис. 2.13
Решение. Система имеет две степени свободы. В качестве обобщенных координат выберем перемещение q 1 = s центра масс С цилиндра 1 и угол q 2 = jповорота стержня 2 (против хода часовой стрелки). Полагаем, что при s = 0 иj = 0 пружины не деформированы. Уравнения Лагранжа второго рода для данной системы имеют вид
Кинетическая энергия системы складывается из кинетических энергий: цилиндра 1 и стержня 2, совершающих плоское движение; ползунов 3 и 4, совершающих поступательное движение: Кинетическая энергия цилиндра 1 Кинетическая энергия стержня 2 венный центр скоростей (МЦС) стержня 2. Принимая во внимание, что Ползуны движутся поступательно и, следовательно,
Таким образом, кинетическая энергия системы, выраженная через обобщенные координаты и обобщенные скорости, равна
Вычисляем производные от кинетической энергии системы: – по q 1 = s – по q 2 = j
Для нахождения обобщенных сил
Эта формула позволяет вычислять обобщенные силы последовательно, учитывая, что обобщенные координаты, а значит, и их вариации не зависят друг от друга. Поэтому системе можно сообщить такое виртуальное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не варьируются. 1. При
где
2. При
где
Выражение в квадратных скобках в уравнении виртуальной работы (2.30) перед вариацией
Подставляя значения производных от кинетической энергии и выражения для обобщенных сил (2.29) и (2.31) в (2.27), получаем дифференциальные уравнения движения системы: по q 1 = s Þ по q 2 = jÞ
Углы Эйлера
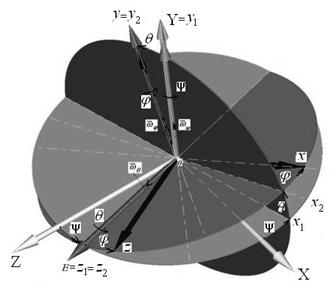
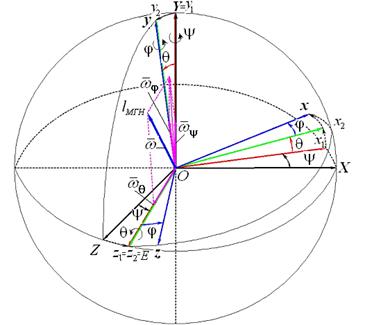
В тех случаях, когда угловая скорость вращения в одном направлении значительно больше, чем в двух других (генераторы, моторы, турбины, гироскопы), для определения положения тела в качестве трех независимых параметров выбирают три угла Эйлера: угол прецессии y (t), угол нутацииq (t) и угол ротации (собственного вращения) j (t). Их названия заимствованы из астрономии. Чтобы задать эти углы, рассмотрим вращение твердого тела вокруг неподвижной точки О. Пусть даны некоторая система отсчета и связанная с ней неподвижная система координат ОXYZ, относительно которой движется твердое тело, и связанная с твердым телом система координат Оxyz, которая движется относительно первой (рис. 3.6 … 3.8). Это означает, что первая и вторая системы координат имеют общее начало O, а углы, образуемые осями Оxyz с осями ОXYZ, изменяются, т.е. система Оxyz
Рис. 3.6
Рис. 3.7 Плоскость ОXZ (заштрихованный овал) пересекает плоскость Оxz (белый овал) по некоторой (рис. 3.8) прямой Оz (1) = Оz (2) = OE, образующей угол y с неподвижной осью ОZ, и угол j с подвижной осью Оz, которая называется «линией узлов» ОЕ с единичным ортом
Рис. 3.8
Неподвижная ось ОY,вокруг которойповорачивается твердое тело на угол прецессииy, называется осью прецессии с единичным ортом Изменение угла нутацииq сопровождается вращением твердого тела вокруг линии узлов Оz 1 = Оz 2 = OE, называемой осью нутации. Наконец, угол ротации (собственного вращения)j характеризует вращение тела вокруг оси Oy = Oy 2, называемой осью ротации (собственного вращения) с единичным ортом На рис 3.6 … 3.8 все углы положительные, т.е. против хода часовой стрелки, если смотреть на поворот тела с положительных направлений осей вращения OY, OE и Oy. Движение твердого тела в любой момент времени полностью определяется положением подвижной связанной с твердым телом системы координат Оxyz относительно неподвижной системы координат ОXYZ, т.е. заданием кинематических уравнений вращения тела вокруг неподвижной точки О: угла прецессии
3.3.Формулы преобразования координат. Поворотные матрицы
Для любой точки М тела с координатами x, y, z в подвижной системе координат Оxyz, жестко связанной с ним, и с ее же координатами X, Y, Z в неподвижной системе координат ОXYZ в соответствии с (3.10), взаимосвязь проекций вектора точки
или где Переход от осей системы[ X ]н к осям системы [ x 1] осуществляется поворотом на угол прецессии ψвокруг неподвижной OY – оси прецессии системы [ X ]н (рис. 3.9 … 3.11). Переход от осей системы[ x 1] к осям системы[ x 2] осуществляется поворотом на уголнутации θ вокруг оси
Рис. 3.9
Переход от осей системы [ x 2] к осям системы[ x ]п– поворотом на уголротации (собственного вращения) φвокруг оси
а б в
Рис. 3.10
Формулы преобразования координат получаем, рассмотрев переход от системы ОXYZ ([ X ]н) к системе Оxyz ([ x ]п), выполненный с помощью трех поворотов: 1. Поворота системы ОXYZ вокруг второй из координатных осей ОY на угол прецессии ψ, т.е. [ X ]н®[ x 1], ОXYZ ® X = x 1 cos y + 0 + z 1 sin y, Y = 0 + y 1 + 0, Z = - x 1 sin y + 0 + z 1 cos y, или в матричной форме [ X ] ={a2y} т [ x 1], (3.16) где поворотная матрица {a2y} т = описывает поворот вокруг второй оси ОY на угол прецессии ψ.
а б
Рис. 3.11
2. Поворота системы Формулы преобразования координат, как видно из рис. 3.11, б, при этом таковы: x 1 = x 2 cos q - y 2 sin q + 0, y 1 = x 2 sin q + y 2 cos q + 0, z 1 = 0 + 0 + z 2, или в матричной форме [ x 1] = {a3q } т [ x 2], (3.18) где матрица {a3q } т = описывает поворот вокруг оси 0z 1 на угол нутации q. 3. Поворота системы
|
|||||||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.012 с.) |



 (2.1)
(2.1)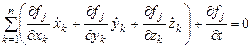 . (2.2)
. (2.2) Решение. Уравнения связей имеют вид
Решение. Уравнения связей имеют вид  где j – угол поворота диска (j=0 при x c = 0). Из первого уравнения связи следует, что
где j – угол поворота диска (j=0 при x c = 0). Из первого уравнения связи следует, что  . Интегрируя второе уравнение, находим связь между координатой xc и углом поворота диска:
. Интегрируя второе уравнение, находим связь между координатой xc и углом поворота диска:  .
. (2.3)
(2.3)
 , где С МЦС– точка соприкосновения шара с плоскостью.
, где С МЦС– точка соприкосновения шара с плоскостью. Интегрирование последнего уравнения дает полученное выше геометрическое условие zс = r.
Интегрирование последнего уравнения дает полученное выше геометрическое условие zс = r.



 , является голономной и стационарной. Для голономной нестационарной связи уравнение имеет вид
, является голономной и стационарной. Для голономной нестационарной связи уравнение имеет вид 


 Пример 2.3. Жесткий стержень длиной l, прикрепленный к неподвижной шарнирной опоре и перемещающийся в плоскости xOy (рис. 2.3), является стационарной связью для материальной точки М, находящейся на его свободном конце. Уравнения связи в декартовой системе координат, начало которой совпадает с точкой закрепления стержня, имеют вид 1) z = 0;2) x 2 + y 2- l 2 = 0.
Пример 2.3. Жесткий стержень длиной l, прикрепленный к неподвижной шарнирной опоре и перемещающийся в плоскости xOy (рис. 2.3), является стационарной связью для материальной точки М, находящейся на его свободном конце. Уравнения связи в декартовой системе координат, начало которой совпадает с точкой закрепления стержня, имеют вид 1) z = 0;2) x 2 + y 2- l 2 = 0. Пример 2.4. Если длина стержня изменяется по заданному закону (рис. 2.4), то связь является нестационарной и уравнения связей имеют вид 1) z = 0; 2) x 2 + y 2- l 2(t)£ 0.
Пример 2.4. Если длина стержня изменяется по заданному закону (рис. 2.4), то связь является нестационарной и уравнения связей имеют вид 1) z = 0; 2) x 2 + y 2- l 2(t)£ 0. . (2.12)
. (2.12) (i = s) и (2.11), а виртуальное перемещение k- й точки
(i = s) и (2.11), а виртуальное перемещение k- й точки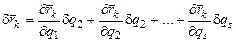 ;
;  .
. в формулу для виртуальной работы сил (2.12), получаем
в формулу для виртуальной работы сил (2.12), получаем . (2.13)
. (2.13) (2.14)
(2.14) . (2.15)
. (2.15) Обобщенная координата определяет и единицу измерения соответствующей обобщенной силы. Из (2.15) следует, что единица измерения обобщенной силыравна единице измерения работы, деленной на единицу измерения обобщенной координаты. Если в качестве обобщенной координаты q принять q = s – перемещение какой-либо точки, то единица измерения обобщенной силы
Обобщенная координата определяет и единицу измерения соответствующей обобщенной силы. Из (2.15) следует, что единица измерения обобщенной силыравна единице измерения работы, деленной на единицу измерения обобщенной координаты. Если в качестве обобщенной координаты q принять q = s – перемещение какой-либо точки, то единица измерения обобщенной силы  =
=  .
.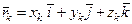 , получаем
, получаем . (2.16)
. (2.16) – вертикальная, а
– вертикальная, а  – горизонтальная силы.
– горизонтальная силы. .
.
 . (2.17)
. (2.17) и
и 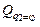 для системы (рис. 2.11). Масса груза 1 равна m 1, массацилиндра 2 равна m 2, а его радиус r. Нить по блоку 3 и цилиндру 2 не скользит. Центр масс цилиндра 2 движется вдоль вертикали.
для системы (рис. 2.11). Масса груза 1 равна m 1, массацилиндра 2 равна m 2, а его радиус r. Нить по блоку 3 и цилиндру 2 не скользит. Центр масс цилиндра 2 движется вдоль вертикали. зададим приращение d s ¹ 0координате груза 1, а для угла jповорота цилиндра 2, будем считать j =const,т.е. dj =0. При этом центр масс цилиндра 2 будет иметь перемещение, равное перемещению груза. Следовательно,
зададим приращение d s ¹ 0координате груза 1, а для угла jповорота цилиндра 2, будем считать j =const,т.е. dj =0. При этом центр масс цилиндра 2 будет иметь перемещение, равное перемещению груза. Следовательно,
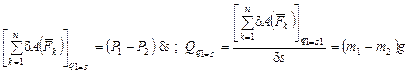 ,
, .
.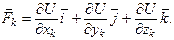
 в (2.17), получаем
в (2.17), получаем

 (2.18)
(2.18)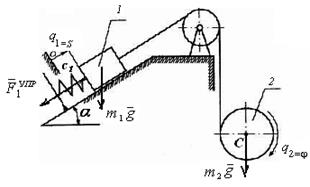
 и
и  .
.
 .
. , ее скорость
, ее скорость . (2.19)
. (2.19) , (2.20)
, (2.20) минус частная производная от кинетической энергии системы по обобщенной координате
минус частная производная от кинетической энергии системы по обобщенной координате  равна обобщенной силе
равна обобщенной силе  , соответствующей обобщенной координате
, соответствующей обобщенной координате  .
. (2.21)
(2.21)
 (2.22)
(2.22) . (2.23)
. (2.23)
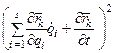 =
= 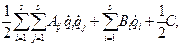 (2.24)
(2.24)
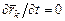 , и тогда Bi = 0, C = 0. В этом случае кинетическая энергия системы является однородной квадратичной формой обобщенных скоростей:
, и тогда Bi = 0, C = 0. В этом случае кинетическая энергия системы является однородной квадратичной формой обобщенных скоростей: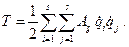 (2.25)
(2.25) и времени, соответствующие левой части уравнений Лагранжа второго рода (2.20), равны
и времени, соответствующие левой части уравнений Лагранжа второго рода (2.20), равны

 то
то
 (2.26)
(2.26) и обобщенные скорости
и обобщенные скорости  .
.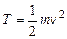 ;
; ;
;  ;
; ;
; ;
; .
.
 . (2.27)
. (2.27) . Так как
. Так как  .
. . Ско-рость центра масс стержня
. Ско-рость центра масс стержня  , где
, где  – мгно-
– мгно- получаем
получаем 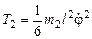 .
.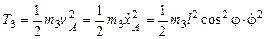 ;
; .
. .
.
 ;
; ;
; .
. и
и  . (2.15 а)
. (2.15 а)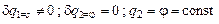
 ,
, , (2.28)
, (2.28) , а выражение в квадратных скобках в (2.28) перед вариацией
, а выражение в квадратных скобках в (2.28) перед вариацией  есть обобщенная сила
есть обобщенная сила . (2.29)
. (2.29)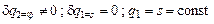
 ,
, (2.30)
(2.30)


 есть обобщенная сила
есть обобщенная сила .(2.31)
.(2.31) ;
;
 .
.
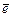 . Кроме того, плоскость Оxz образует с плоскостью ОXZ угол q, равный углу между осями ОY и Оy.
. Кроме того, плоскость Оxz образует с плоскостью ОXZ угол q, равный углу между осями ОY и Оy.
 .
.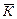 .
. , угланутации
, угланутации  и угларотации (собственного вращении)
и угларотации (собственного вращении)  .
.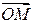 на оси двух систем координат [ X ]н и [ x ]п имеет вид
на оси двух систем координат [ X ]н и [ x ]п имеет вид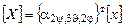 , (3.14)
, (3.14)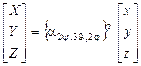 , (3.15)
, (3.15)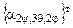 - матрица, транспонированная к матрице направляющих косинусов
- матрица, транспонированная к матрице направляющих косинусов 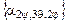 ,задающей преобразование поворота от осей неподвижной системы OXYZ (с базисом [ X ]н)к осям подвижной системы Оxyz (с базисом [ x ]п ), неизменно связанной с телом. Транспонированная матрица
,задающей преобразование поворота от осей неподвижной системы OXYZ (с базисом [ X ]н)к осям подвижной системы Оxyz (с базисом [ x ]п ), неизменно связанной с телом. Транспонированная матрица  системы [ x 1] (рис. 3.5 … 3.11, б).
системы [ x 1] (рис. 3.5 … 3.11, б).
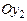 системы[ x 2] .
системы[ x 2] .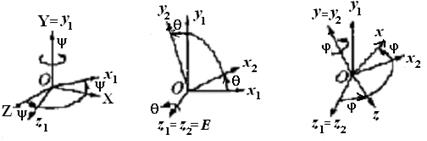
 , причем
, причем 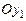
 (рис. 3.9 … 3.11, а). Координаты систем координат ОXYZ и
(рис. 3.9 … 3.11, а). Координаты систем координат ОXYZ и  (3.17)
(3.17)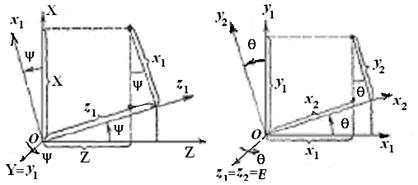
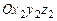 , при этом
, при этом 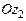 (рис. 3.7,3.9, 3.11, б).
(рис. 3.7,3.9, 3.11, б).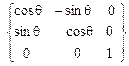 (3.19)
(3.19)


