
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виртуальная работа силы. Идеальные связи
Виртуальной называется работа силы на любом виртуальном перемещении точки ее приложения: d А ( Для вычисления виртуальной работы можно применять известные формулы для элементарной работы силы, подставляя вместо элементарного возможного При использовании декартовых координат d А ( Например,виртуальная работа горизонтальной силы Если к твердому телу, вращающемуся вокруг неподвижной оси l = Oz,приложена сила d А ( где dj - виртуальное угловое перемещение тела вокруг оси l =Oz. d А ( где F t – проекция силы на направление касательной, d s – вариация траекторной координаты точки приложения силы при траекторном способе задания ее движения. d А ( где Fv – проекция силы на направление скорости точки приложения силы, d S – вариация перемещения точки приложения силы. Виртуальная работа потенциальных сил равна вариации силового потенциала d А = d U или вариации со знаком минус потенциальной энергии системы d А = - dП. Установив понятие виртуальной работы силы, можно расширить классификацию связей, разделяя их на идеальные и неидеальные. Связи называются идеальными, если равна нулю сумма виртуальных работ реакций этих связей на любом виртуальном перемещении системы (из занимаемого в данный момент времени положения). Для идеальных связей или Полагая связи идеальными, можно решить задачу динамики несвободной системы, которая состоит в том, что для данной системы с заданными активными силами и начальными условиями нужно найти уравнения движения и реакции связей. Например,если материальная точка движется по гладкой поверхности, уравнение которой f (x, y, z)= 0, то нормальная реакция Уравнения связи совместно с дифференциальными уравнениями движения точки образуют замкнутую систему уравнений, позволяющую определить как уравнения движения точки, так и множитель Лагранжа, а значит, и нормальную реакцию связи
Примеры идеальных связей: 1. Гладкая поверхность (плоскость)для материальной точки. В этом случае d А (
2. Нерастяжимая нить. Реакция нити – сила ее натяжения ортогональна виртуальному перемещению точки ее приложения, поэтому d А (
4. Твердая шероховатая поверхность для цилиндрического катка при качении без скольжения. Контакт катка с поверхностью происходит по линии. Поэтому реакцией связи является система сил, распределенных вдоль линии контакта. Виртуальная работа сил реакции равна нулю, так как они приложены к неподвижным в каждый момент времени точкам СМЦС сечений катка (см. рис. 2.1). Обобщенные силы В аналитической механике, наряду с понятием о силе как векторной величине, характеризующей воздействие на данное тело других материальных тел, используют понятие об обобщенной силе. Для определения обобщенной силы рассмотрим виртуальную работу сил, приложенных к точкам системы,
Если механическая система при наложенных на нее голономных удерживающих h связях имеет s = 3 n - h степеней свободы, то ее положение определяется обобщенными координатами
Подставляя
Скалярную величину
называют обобщенной силой, соответствующей i -й обобщенной координате. Подставляя (2.14) в (2.13), получаем формулу для виртуальной работы
Обобщенной силой, соответствующей i - й обобщенной координате, называется множитель при вариации данной обобщенной координаты в выражении виртуальной работы сил, действующих на механическую систему. Виртуальная работа определяется от задаваемых активных сил, независящих от ограничений, и реакций связей (если связи не идеальны, то для решения задачи необходимо дополнительно задать физическую зависимость Tj от Nj (Tj – это, как правило, силы трения или моменты сопротивления трению качения, которые мы умеем определять).
В общем случае обобщенная силаявляется функцией обобщенных координат, скоростей точек системы и времени. Из формулировки следует, что обобщенная сила – скалярная величина, которая зависит от выбранных для данной механической системы обобщенных координат. Это значит, что при изменении набора обобщенных координат, определяющих положение данной системы, изменятся и обобщенные силы. Пример 2.10. Для диска радиусом r и массой m, который катится без скольжения по наклонной плоскости (рис. 2.9), за обобщенную координату можно принять: либо q = s - перемещение центра масс диска, либо q = j - угол поворота диска. Если пренебречь сопротивлением качению, то в первом случае обобщенной силой будет Qs = mg sina, а во втором - Q j = mg r sina.
Существуют различные способы вычисления обобщенных сил. 1. Согласно (2.14), обобщенная сила
Принимая во внимание, что
Этот способ определения обобщенных сил называют аналитическим. Пример 2.11. Найти обобщенную силу Qq= j, если в кривошипно-ползунном механизме (рис. 2.10) OA=AB= l, Решение. Так как F 1 x= 0и F 2 y= 0, то обобщенная сила согласно (2.16)
Проекции сил и координаты точек их приложения определяются как F 1 y=- F 1; F 2 x=- F 2; yA = l sinj; xB = 2 l cosj. Следовательно, Qq= j= - F 1 l cosj + 2 F 2 l sinj.
Рис. 2.10
2. Укажем на более простой способ вычисления обобщенной силы. Обобщенные силы для механических систем с числом степеней свободы s=k > 1целесообразно вычислять последовательно, учитывая, что обобщенные координаты, а значит, и их вариации тоже не зависят друг от друга. Системе всегда можно сообщить такое виртуальное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не варьируются. В этом случае из (2.15) получаем
Индекс qi в (2.17) означает, что виртуальная работа сил, действующих на систему, определяется на перемещениях точек приложения этих сил, соответствующих вариации только одной i- йобобщенной координаты. Пример 2.12. Найти обобщенные силы Решение. Для определе-ния обобщенной силы
где P 1 =m 1 g; P 2 =m 2 g. Определяя
3. Если силы, действующие на механическую систему, потенциальные, то для определения обобщенных силможно использовать силовую функцию U или потенциальную энергию П системы.
Потенциальная сила
Подставляя проекции силы Так как U = - П,то
Пример 2.13. В системе, показанной на рис. 2.12, массы груза 1 и цилиндра 2 равны m 1и m 2соответственно, радиус цилиндра r, а коэффициент жесткости пружины с 1 .
Рис. 2.12
Полагая, что трение между грузом и наклонной плоскостью отсутствует, а траектория точки С – центра масс цилиндра – вертикаль, найти обобщенные силы Решение. Потенциальная энергия системы
Обобщенные силы, соответствующие обобщенным координатам:
2.7. Уравнения Лагранжа II рода (без вывода) Уравнения Лагранжа второго рода представляют собой дифференциальные уравнения движения несвободной механической системы, составленные в обобщенных координатах. Рассматривается движение системы, состоящей из n материальных точек относительно инерциальной системы отсчета. Наложенные на систему h связей – голономные, удерживающие, нестационарные. Если связи неидеальные, то соответствующие им реакции следует добавить к действующим на систему активным силам. Пусть система имеет s = 3 n – h степеней свободы и ее положение определяется q 1, q 2, …, qi, …, qs обобщенными координатами, а радиус-вектор любой точки этой системы - формулой (2.11): Виртуальноеперемещение k -й точки
Уравнения Лагранжа второго рода формулируются следующим образом:
где T – кинетическаяэнергия механической системы; число уравнений Лагранжа II рода равно i = s числу степеней свободы системы; т.е. полная производная по времени d/dt от частной производной от кинетической энергии системы по обобщенной скорости В уравнения Лагранжа не входят заранее неизвестные реакции идеальных связей. Если силы, действующие на систему, потенциальные, то обобщенные силы находятся по формуле (2.18), а уравнения Лагранжа второго рода в этом случае преобразуются к виду
Функция, равная разности кинетической и потенциальных энергий механической системы, называется функцией Лагранжа L = T – П. Так как потенциальная энергия системы является функцией только обобщенных координат, то
При использовании функции Лагранжа уравнения(2.21) принимают вид
Кинетическая энергия механической системы, состоящей из n материальных точек, как известно, определяется по формуле
Принимая во внимание выражение (2.19), кинетическую энергию системы можно записать в виде
где
Если наложенные на систему связи стационарные, то
Производные от кинетической энергии (2.25) по обобщенной скорости
Так как
Подставляя эти выражения в уравнение Лагранжа (2.20), получаем
Так как обобщенные силы - функции обобщенных координат, времени и, возможно, обобщенных скоростей, то каждое из уравнений (2.26) имеет второй порядок. Порядок уравнений не изменится и при нестационарных связях, так как в этом случае в выражения (2.26) войдут слагаемые, зависящие только от обобщенных координат, обобщенных скоростей и времени. Таким образом, уравнения Лагранжа второго рода для механической системы с голономными связями представляют собой систему обыкновенных дифференциальных уравнений порядка 2 n относительно обобщенных координат. Уравнения Лагранжа второго рода сыграли решающую роль в развитии динамики систем и широко используются для решения многих задач динамики многопараметрических систем. Следует отметить, что для понимания существа и особенностей метода Лагранжа недостаточно изучения одной теории, необходимо рассматривать много примеров и задач. Изучение уравнений Лагранжа должно быть предметным. 2.8. Последовательность действий при использовании
1.Определить число степеней свободы системы и выбрать наиболее удобные обобщенные координаты. 2. Вычислить кинетическую энергию системы в ее абсолютном движении и выразить эту энергию через обобщенные координаты Напомним формулы кинетических энергий в абсолютном движении: · для материальной точки · длясистемы материальных точек · длятвердого тела: – при поступательном движении – при вращении вокруг неподвижной оси l – при плоскопараллельном движении
– при вращении вокруг неподвижной точки – в общем случае движения твердого тела
3. Вычислить производные от кинетической энергии, входящие в левую часть уравнений Лагранжа. 4. Определить обобщенные силы, соответствующие выбранным обобщенным координатам (так как каждой обобщенной координате соответствует обобщенная сила, то число обобщенных сил механической системы равно числу обобщенных координат, причем размерность каждой из обобщенных сил соответствует размерности соответствующей обобщенной координаты). 5. Подставить все вычисленные величины в уравнения Лагранжа. Пример 2.14. Механическая система (рис. 2.13) состоит из однородного круглого цилиндра 1 массой m 1 и радиусом r, однородного стержня 2 длиной l и массой m 2, к которому в точках А и В шарнирно прикреплены ползуны 3 и 4 массами m 3и m 4, а также двух пружин с коэффициентами жесткости С 1 и С 2. Цилиндр без скольжения катится по горизонтальной плоскости. К нему приложена пара сил с моментом М 1(t).
Пренебрегая сопротивлением качению цилиндра 1, трением в шарнирах и направляющих, а также массой пружин, составить дифференциальные уравнения движения системы.
Рис. 2.13
Решение. Система имеет две степени свободы. В качестве обобщенных координат выберем перемещение q 1 = s центра масс С цилиндра 1 и угол q 2 = jповорота стержня 2 (против хода часовой стрелки). Полагаем, что при s = 0 иj = 0 пружины не деформированы. Уравнения Лагранжа второго рода для данной системы имеют вид
Кинетическая энергия системы складывается из кинетических энергий: цилиндра 1 и стержня 2, совершающих плоское движение; ползунов 3 и 4, совершающих поступательное движение: Кинетическая энергия цилиндра 1 Кинетическая энергия стержня 2 венный центр скоростей (МЦС) стержня 2. Принимая во внимание, что Ползуны движутся поступательно и, следовательно,
Таким образом, кинетическая энергия системы, выраженная через обобщенные координаты и обобщенные скорости, равна
Вычисляем производные от кинетической энергии системы: – по q 1 = s – по q 2 = j
Для нахождения обобщенных сил
Эта формула позволяет вычислять обобщенные силы последовательно, учитывая, что обобщенные координаты, а значит, и их вариации не зависят друг от друга. Поэтому системе можно сообщить такое виртуальное перемещение, при котором изменяется только одна обобщенная координата, а другие при этом не варьируются. 1. При
где
2. При
где
Выражение в квадратных скобках в уравнении виртуальной работы (2.30) перед вариацией
Подставляя значения производных от кинетической энергии и выражения для обобщенных сил (2.29) и (2.31) в (2.27), получаем дифференциальные уравнения движения системы: по q 1 = s Þ по q 2 = jÞ
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-19; просмотров: 533; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.97.64 (0.112 с.) |
 ) =
) =  .
. виртуальное
виртуальное  перемещение точки.
перемещение точки. , приложенной к стержню АВ (рис. 2.7) в точке С,равна d А (
, приложенной к стержню АВ (рис. 2.7) в точке С,равна d А (
 .
.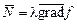 ,гдеl – неопределенный множитель Лагранжа.
,гдеl – неопределенный множитель Лагранжа.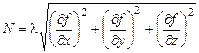 .
. )=
)=  ) = 0, так как вектор
) = 0, так как вектор 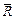 расположен вдоль нормали к поверхности и, следовательно, ортогонален вектору
расположен вдоль нормали к поверхности и, следовательно, ортогонален вектору  3. Цилиндрические и сферические шарниры, если поверхности соприкасающихся тел считаются идеально гладкими. Если твердое тело при помощи шарнира прикреплено к неподвиж-
3. Цилиндрические и сферические шарниры, если поверхности соприкасающихся тел считаются идеально гладкими. Если твердое тело при помощи шарнира прикреплено к неподвиж- = 0 и др.
= 0 и др. . (2.12)
. (2.12) (i = s) и (2.11), а виртуальное перемещение k- й точки
(i = s) и (2.11), а виртуальное перемещение k- й точки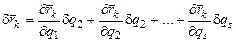 ;
;  .
. в формулу для виртуальной работы сил (2.12), получаем
в формулу для виртуальной работы сил (2.12), получаем . (2.13)
. (2.13) (2.14)
(2.14) . (2.15)
. (2.15) Обобщенная координата определяет и единицу измерения соответствующей обобщенной силы. Из (2.15) следует, что единица измерения обобщенной силыравна единице измерения работы, деленной на единицу измерения обобщенной координаты. Если в качестве обобщенной координаты q принять q = s – перемещение какой-либо точки, то единица измерения обобщенной силы
Обобщенная координата определяет и единицу измерения соответствующей обобщенной силы. Из (2.15) следует, что единица измерения обобщенной силыравна единице измерения работы, деленной на единицу измерения обобщенной координаты. Если в качестве обобщенной координаты q принять q = s – перемещение какой-либо точки, то единица измерения обобщенной силы  =
=  .
.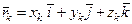 , получаем
, получаем . (2.16)
. (2.16) – вертикальная, а
– вертикальная, а  – горизонтальная силы.
– горизонтальная силы. .
.
 . (2.17)
. (2.17) и
и 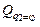 для системы (рис. 2.11). Масса груза 1 равна m 1, массацилиндра 2 равна m 2, а его радиус r. Нить по блоку 3 и цилиндру 2 не скользит. Центр масс цилиндра 2 движется вдоль вертикали.
для системы (рис. 2.11). Масса груза 1 равна m 1, массацилиндра 2 равна m 2, а его радиус r. Нить по блоку 3 и цилиндру 2 не скользит. Центр масс цилиндра 2 движется вдоль вертикали. зададим приращение d s ¹ 0координате груза 1, а для угла jповорота цилиндра 2, будем считать j =const,т.е. dj =0. При этом центр масс цилиндра 2 будет иметь перемещение, равное перемещению груза. Следовательно,
зададим приращение d s ¹ 0координате груза 1, а для угла jповорота цилиндра 2, будем считать j =const,т.е. dj =0. При этом центр масс цилиндра 2 будет иметь перемещение, равное перемещению груза. Следовательно,
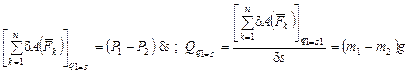 ,
, .
.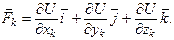
 в (2.17), получаем
в (2.17), получаем

 (2.18)
(2.18)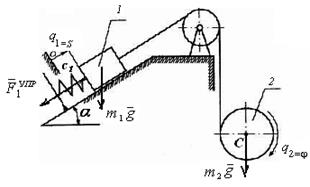
 и
и  .
.
 .
. , ее скорость
, ее скорость . (2.19)
. (2.19) , (2.20)
, (2.20) минус частная производная от кинетической энергии системы по обобщенной координате
минус частная производная от кинетической энергии системы по обобщенной координате  равна обобщенной силе
равна обобщенной силе  , соответствующей обобщенной координате
, соответствующей обобщенной координате  .
. (2.21)
(2.21)
 (2.22)
(2.22) . (2.23)
. (2.23)
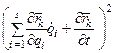 =
= 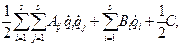 (2.24)
(2.24)
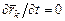 , и тогда Bi = 0, C = 0. В этом случае кинетическая энергия системы является однородной квадратичной формой обобщенных скоростей:
, и тогда Bi = 0, C = 0. В этом случае кинетическая энергия системы является однородной квадратичной формой обобщенных скоростей: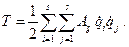 (2.25)
(2.25) и времени, соответствующие левой части уравнений Лагранжа второго рода (2.20), равны
и времени, соответствующие левой части уравнений Лагранжа второго рода (2.20), равны

 то
то
 (2.26)
(2.26) и обобщенные скорости
и обобщенные скорости  .
.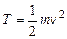 ;
; ;
;  ;
; ;
; ;
; .
.
 . (2.27)
. (2.27) . Так как
. Так как  .
. . Ско-рость центра масс стержня
. Ско-рость центра масс стержня  , где
, где  – мгно-
– мгно- получаем
получаем 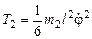 .
.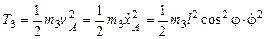 ;
; .
. .
.
 ;
; ;
; .
. и
и  . (2.15 а)
. (2.15 а)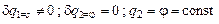
 ,
, , (2.28)
, (2.28) , а выражение в квадратных скобках в (2.28) перед вариацией
, а выражение в квадратных скобках в (2.28) перед вариацией  есть обобщенная сила
есть обобщенная сила . (2.29)
. (2.29)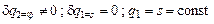
 ,
, (2.30)
(2.30)


 есть обобщенная сила
есть обобщенная сила .(2.31)
.(2.31) ;
;
 .
.


