
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достижение точности замыкающего звена РЦ методами полной и неполной взаимозаменяемостиСодержание книги
Поиск на нашем сайте
Расчет размерных цепей методом максимума-минимума
Для расчета размерных цепей существуют два метода: метод максимума и минимума и метод, основанный на теории вероятностей. Расчет РЦ по методу максимума-минимума основан на предположении, что на сборку изделия поступают детали с предельными размерами и при том в таком сочетании, что в размерной цепи все увеличивающие звенья имеют наибольшие предельные размеры, а все уменьшающие звенья - наименьшие предельные размеры, или наоборот. В результате этого размер замыкающего звена получит либо максимальное, либо минимальное значение. Такой случай, конечно, возможен, но вероятность его существенно мала. В связи с этим этот метод расчёта должен иметь ограниченное применение. В частности им пользуются при числе составляющих звеньевm-1≤ 4, а также приm-1 ≥ 5 для изделий с единичным производством для предварительных решений многозвенных цепей. В курсовой работе этот метод используют для многозвенных цепей в учебных целях. В основе расчёта лежит положение о том, что поле допуска замыкающего звена ТΔ плоской размерной цепи с параллельными звеньями равна сумме значений полей допусков всех составляющих звеньев Ti:
где Ɛ1- передаточное отношение 1-го составляющего звена; для плоских цепей с параллельными звеньями Ɛ1 =1 для увеличивающих звеньев, Ɛ1=1 для уменьшающих составляющих звеньев; i=1,2,3,..., m-1- порядковый номер составляющего звена. При суммировании допусков учитывают абсолютные значения передаточных отношений, т, к. значения полей допусков всегда положительны. Поэтому Ɛ1=1
Таким образом, поле допуска замыкающего звена размерной цепи с параллельными звеньями равно сумме абсолютных значений полейдопусков всех составляющих звеньев. Аналогичная связь существует между полем рассеяния замыкающего звена ѠΔ полем рассеяния значений составляющих звеньев:
Для плоских размерных цепей с параллельными звеньями
Уравнение размерной цепи для номинальных размеров в общем виде можно записать так:
Координата середины поля допуска замыкающего звена плоской размерной цепи с параллельными звеньями равна алгебраической сумме координат середин полей допусков составляющих звеньев с учётом их собственных знаков, т. е
или
Все рассуждения, касающиеся координат середины полей допусков, в полной мере распространяются и на координаты середин полей рассеяния. Поэтому по аналогии будем иметь
или
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-10; просмотров: 190; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.25.222 (0.009 с.) |

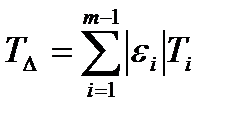 (10.1)
(10.1)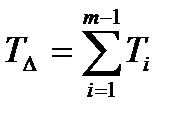 . (10.2)
. (10.2)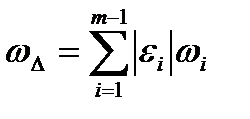 (10.3)
(10.3) (10.4)
(10.4) (10.5)
(10.5) (10.6)
(10.6)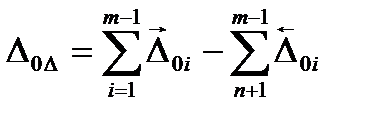 . (10.7)
. (10.7) (10.8)
(10.8) (10.9)
(10.9)


