Практикум по синтезу и минимизации логических функций.

Задача 1.2.

Полностью определённая булева функция от 4-х переменных задана десятичными рабочими наборами: РН(4) = 5, 6, 7, 8, 9, 10, 11.Число в скобках указывает количество переменных. Найти минимальную форму этой функции.

Решение.

Так как функция является полностью определённой, то запрещёнными наборами ЗН(4) являются наборы 0 - 4, 12 - 15. Исходя из этой информации, составляем таблицу истинности и осуществляем минимизацию по карте Карно.

 

Таблица 4.

 

РН(4)	x4 x3 x2 x1	f
	0 1 0 1
	0 1 1 0
	0 1 1 1
	1 0 0 0
	1 0 0 1
	1 0 1 0
	1 0 1 1

 

ЗН(4)	x4 x3 x2 x1	f
	0 0 0 0
	0 0 0 1
	0 0 1 0
	0 0 1 1
	0 1 0 0
	1 1 0 0
	1 1 0 1
	1 1 1 0
	1 1 1 1

 

По карте Карно получаем результат: f = x₄x₃’ + x₄’x₃(x₁ + x₂)

 

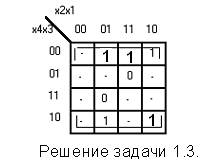
Задача 1.3.

Найти минимальную форму функции y, представленной на рисунке.

Решение.

Функция задана только на 7 наборах. Добавим к пяти рабочим наборам ещё три, а именно: 0000, 1000, 1011. Все оставшиеся наборы доопределим как запрещённые. В результате такого доопределения получим прямоугольник Карно, состоящий из 8 элементарных квадратов Карно. Этому прямоугольнику соответствует функция: y = x₃’

 

 

Задача 1.4.

Построить преобразователь двоичного кода в двоично-десятичный в соответствии с таблицей.

x4x3x2x1	y5y4y3y2y1	x4x3x2x1	y5y4y3y2y1
0 0 0 0	0 0 0 0 0	0 1 1 0	0 0 1 1 0
0 0 0 1	0 0 0 0 1	0 1 1 1	0 0 1 1 1
0 0 1 0	0 0 0 1 0	1 0 0 0	0 1 0 0 0
0 0 1 1	0 0 0 1 1	1 0 0 1	0 1 0 0 1
0 1 0 0	0 0 1 0 0	1 0 1 0	1 0 0 0 0
0 1 0 1	0 0 1 0 1	1 0 1 1	1 0 0 0 1

 

Решение.

Для каждой функции y_i заполняем карту Карно, производим доопределение и осуществляем минимизацию. Весь процесс отражён на рисунке.

В результате минимизации получаем систему функций:

y₁ = x₁ y₂ = x₄’x₂ y₃ = x₃ y₄ = x₄x₂’ y₅ = x₄x₂

Задача 1.5.

Построить один разряд многоразрядного сумматора, заданного таблицей истинности. Здесь a_i и в_i - значения i-ых разрядов слагаемых а и в, P_i и S_i - значения переноса и суммы на выходе i-го разряда, P_i-1 - значение переноса на выходе предыдущего разряда.

 

ai вi Pi-1	Pi	Si
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

 

Решение.

Имеем систему полностью определённых булевых функций. Производим раздельную минимизацию каждой функции (см. рисунок).

Из карт Карно после минимизации получаем следующие результаты.

S_i = a_i’в_i’P_i-1 + a_i’в_iP_{i-1’ + ai}в_i’P_{i-1’ + ai}в_iP_i-1

P_i = в_iP_i-1 + a_iP_i-1 + a_iв_i

Законы логики суждений

Суждение – это повествовательное предложение, которое может быть истинным или ложным. Логика суждений изучает законы правильных рассуждений. Автор не открывает здесь ничего нового, но, излагая данный материал, хочет показать всю простоту выводов данных законов, следовательно, и их никчёмность: незачем заучивать десятки правил, если доказательство столь примитивно. Всё дело в том, что в классической логике доказательство построено на громоздком аппарате таблиц истинности, а мы будем использовать формулу импликации и карту Карно.

Алгоритм «Импульс».

Алгоритм инженерного анализа законов логики суждений чрезвычайно прост:

1)произвести замену всех знаков импликации на символы дизъюнкции в соответствии с известной формулой x ® y = x’ + y;

2)привести полученное выражение к ДНФ;

3)занести ДНФ в карту Карно и убедиться, что она вся покрыта единицами – это свидетельствует об истинности проверяемого закона или суждения.

Воспользуемся перечнем импликативных законов для проверки алгоритма «Импульс».