Русская логика в информатике (букварь математической логики).

Русская логика в информатике (Букварь математической логики).

Аннотация

Данная брошюра в популярной форме знакомит читателей с наиболее значимыми разделами Русской логики, которая опровергает многие постулаты классической логики, являясь на сегодня единственной истинно математической логикой. Автор обвиняет современных матлогиков в невежестве и безграмотности. Брошюра рассчитана на школьных преподавателей математики и информатики, но может быть освоена и школьниками 5-7-ых классов. Брошюра весьма полезна преподавателям и студентам вузов, а также всем профессорам и академикам.

Предисловие

Знает ли хоть кто-нибудь математическую логику? Вы сами ответите на этот вопрос, пройдя тестирование по следующему вопроснику.

Вопросник для математика и логика.

Как работать с картой Карно на 8 и более переменных?

Что такое метод обобщённых кодов Мавренкова?

Что можно вычислить с помощью кванторного исчисления?

Алгебра множеств и алгебра логики. Назовите различия.

Логика предикатов и логика суждений. В чём разница?

Физический смысл и вывод формулы импликации.

Фигуры и модусы Аристотеля. В чём их практическая ценность?

Правильны ли правила посылок в силлогистике?

Как выглядят аналитические представления для Axy, Exy и Ixy?

В чём смысл логики П.С. Порецкого?

В чём главное достижение логики Л. Кэрролла?

Что такое вероятностная логика?

Что такое 4-значная комплементарная логика?

Как решаются логические уравнения?

Что такое логическое вычитание и деление?

Алгебра логики

Синтез логических функций

Под синтезом логических функций будем понимать процесс её получения по словесному описанию, по таблице истинности или любому другому способу задания этой функции. Синтез логических функций можно проиллюстрировать решением простой задачи.

Задача 1.1.

Приёмная комиссия в составе трех членов комиссии и одного председателя решает судьбу абитуриента большинством голосов. В случае равного распределения голосов большинство определяется голосом председателя. Найти краткое определение ситуации, в которой абитуриент будет принят в учебное заведение. Найти решение в виде логической функции, т.е. построить автомат для тайного голосования.

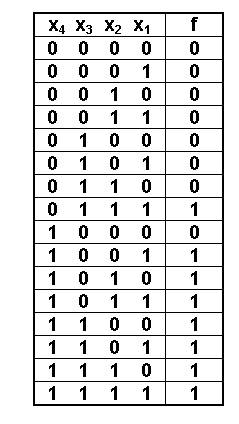
Решение.

Пусть f - функция большинства голосов. f = 1, если большинство членов комиссии проголосовало за приём абитуриента, и f = 0 в противном случае.

Обозначим через x₄ голос председателя комиссии. x₄ = 1, если председатель комиссии проголосовал за приём абитуриента. x₃, x₂, x₁ - голоса членов приёмной комиссии.

С учётом вышеуказанных допущений условие задачи можно однозначно представить в виде таблицы истинности.

Заполнение таблицы осуществляем с учётом того, что функция f является полностью определённой, т.е. она определена на всех возможных наборах переменных x₁ - x₄. Для n входных переменных существует N = 2ⁿ наборов переменных. В нашем примере N = 2⁴ = 16 наборов.

Записывать эти наборы можно в любом порядке, но лучше в порядке возрастания двоичного кода.

Примечание. Здесь и далее под набором будем понимать конъюнкцию, т.е. логическое произведение, всех входных переменных.

Все наборы, на которых функция принимает значение 1, будем называть единичными, или рабочими. Наборы, на которых функция принимает значение 0, будем называть нулевыми, или запрещенными (по Мавренкову Л.Т.).

Для того, чтобы по таблице истинности найти функцию f, достаточно выписать все единичные наборы и соединить их знаком дизъюнкции.

 

Таким образом,

f = 0111+1001+1010+1011+1100+1101+1110+1111

или в символьном виде

f = x₄’x₃x₂x₁+x₄x₃’x₂’x₁+x₄x₃’x₂x₁’+x₄x₃’x₂x₁+x₄x₃x₂’x₁’+x₄x₃x₂’x₁+

+x₄x₃x₂x₁’+x₄x₃x₂x₁

Полученная форма функции называется совершенной дизъюнктивной нормальной формой (СДНФ), здесь каждое логическое слагаемое представляет собой конъюнкцию всех аргументов. В случае, когда не каждое слагаемое представляет собой конъюнкцию всех аргументов, то такая форма представления логической функции называется просто ДНФ. Очевидно, применяя основные законы булевой алгебры, мы могли бы аналитически уменьшить сложность полученного выражения. Но это наихудший способ минимизации булевых функций.

Законы логики суждений

Суждение – это повествовательное предложение, которое может быть истинным или ложным. Логика суждений изучает законы правильных рассуждений. Автор не открывает здесь ничего нового, но, излагая данный материал, хочет показать всю простоту выводов данных законов, следовательно, и их никчёмность: незачем заучивать десятки правил, если доказательство столь примитивно. Всё дело в том, что в классической логике доказательство построено на громоздком аппарате таблиц истинности, а мы будем использовать формулу импликации и карту Карно.

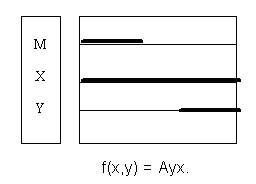
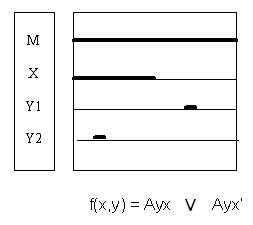
Алгоритм «Импульс».

Алгоритм инженерного анализа законов логики суждений чрезвычайно прост:

1)произвести замену всех знаков импликации на символы дизъюнкции в соответствии с известной формулой x ® y = x’ + y;

2)привести полученное выражение к ДНФ;

3)занести ДНФ в карту Карно и убедиться, что она вся покрыта единицами – это свидетельствует об истинности проверяемого закона или суждения.

Воспользуемся перечнем импликативных законов для проверки алгоритма «Импульс».

Закон Лобановой С.В.

Силлогистика.

Силлогистика – раздел логики, занимающийся анализом и синтезом силлогизмов. Силлогизм – это логическое рассуждение, состоящее из двух посылок, связанных друг с другом общим (средним) термином, и следующего из посылок заключения. В силлогизме обязательно присутствуют 3 термина: один средний и два крайних. Заключение определяет связь крайних терминов друг с другом.

Под анализом мы будем понимать проверку правильности заданного заключения, а под синтезом – нахождение заключения при заданных посылках.

Рассмотрим достаточно очевидный пример силлогизма:

Все люди талантливы.

Все школьники – люди.

Все школьники талантливы.

Здесь общим термином является слово «люди», крайние термины – «талантливые» и «школьники». Это очень простой силлогизм: полученное заключение, связывающее крайние термины, «Все школьники талантливы» не вызывает сомнений. Чуть посложнее задачка – и все «логики» (по саркастическому определению Кэрролла) пасуют. Чтобы ввести математику в силлогистику, пришлось создать скалярные диаграммы (диаграммы Лобанова). На их основе были получены математические соотношения для всех силлогистических функторов (кванторов). Классическая логика различает общеутвердительный (Аху), общеотрицательный (Еху), частноутвердительный (Ixy) и частноотрицательный (Oxy) функторы. Частноотрицательный функтор не имеет смысла, поэтому он нигде не используется. Вышеуказанные обозначения «переводятся на русский язык» следующим образом:

Аху – Все Х суть У. Еху – Ни один Х не есть У.

Ixy – Некоторые Х суть У. Oxy – Некоторые Х не суть У.

Автор в 1995г., создавая Русскую логику, не подозревал (а современные логики и до сих пор не подозревают), что 125 лет тому назад формулы для Axy, Exy очень красиво вывел П.С.Порецкий[11] без всяких диаграмм. На рисунке показаны диаграммы Лобанова, переход к ним от диаграмм Венна и процесс вывода соотношений для Аху, Еху и Ixy.

На диаграммах символ U обозначает универсум. Под универсумом подразумевается мир вещей, понятий и т.п., в среде которых и находятся термины (множества) силлогизма. В вышеприведённом силлогизме в качестве универсума можно выбрать либо млекопитающих, либо всех животных, либо весь животный и растительный мир. Поэтому, задавая силлогизм, нужно обязательно оговаривать универсум.

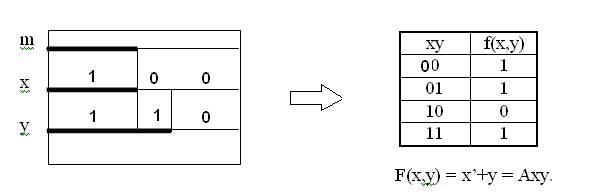
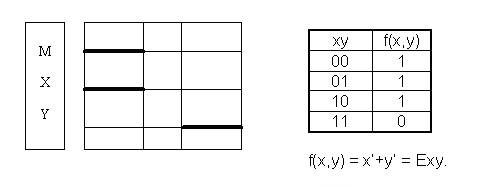
Рассмотрим, как выполняется переход от скалярных диаграмм Лобанова к таблицам истинности на примере синтеза Axy. Из скалярной диаграммы для Axy видно, что аргументы х и y образуют следующие наборы: 00, 01 и 11. Поэтому против них в таблице истинности в графе Axy записаны единицы. Набора 10 не существует, поэтому против него в графе Axy записан нуль. После занесения таблицы истинности в карту Карно и минимизации была получена формула

Axy = x’+y.

Аналогично были получены формулы для Exy, Ixy.

Решение этой же задачи Порецким на основе формулы равнозначности выглядит так: Axy = (x = xy) = x(xy)+x’(xy)’ = xy+x’(x’+y’) = xy+x’ = x’+y.

Здесь (x = xy) означает, что множество Х является пересечением множеств Х и Y. Аналогично по Порецкому Exy = (x = xy’) = xy’+x’(xy’)’ = xy’+x’ = x’+y’. Кстати, отсюда видно, что общеотрицательный функтор не нужен, т.к. Exy = Axy’ = Ayx’, т.е. вполне можно обойтись одним общеутвердительным функтором.

Этих формул до сих пор нет ни в одном учебнике логики.

Из анализа полученных соотношений следует весьма жёсткий вывод.

Логика суждений и логика предикатов (силлогистика) – это одно и то же. Дело в том, что общеутвердительный силлогистический функтор описывается по Порецкому и по Лобанову формулой: Axy = x’ + y.

Импликация имеет тот же математический вид: x→ y = x’ + y.

Да и общеразговорные значения этих операторов одинаковы. Мы говорим: «Все люди талантливы». Этот же смысл сохранится в суждении: «Если ты человек, то ты талантлив». «Во всяком равнобедренном треугольнике углы при основании равны» или «Если треугольник равнобедренный, то углы при основании равны».

Часто задают вопрос:«Почему x→ y = x’ + y?».Именно потому,что x→ y ≡ Axy. Но Порецкий П.С. доказал, что Axy = x’ + y, поэтому и x→ y = x’ + y.

Следовательно, разделение на логику суждений и логику предикатов бессмысленно и свидетельствует о бестолковости современных матлогиков. Ну а математик, не знающий логики – по меньшей мере невежда и, вполне вероятно, что бестолочь. Во всяком случае, ни один математик не возмутился алгеброй множеств, логикой предикатов, кванторным исчислением и другими «находками» матлогиков. Дело в том, что алгебра множеств – это и есть алгебра логики, поскольку логика оперирует и множествами. Кванторное исчисление ничего не исчисляет, т.к. является обыкновенной мнемоникой. А логика предикатов, как мы только что сейчас доказали, и логика суждений – синонимы.

Для решения задач силлогистики автором были разработаны различные алгоритмы. Самый прозрачный и эффективный из них алгоритм «ТВАТ» (Тушинский вечерний авиационный техникум).

Алгоритм «ТВАТ» (графический синтез силлогизмов)

1.Изобразить все возможные ситуации для исходных посылок с помощью скалярных диаграмм.

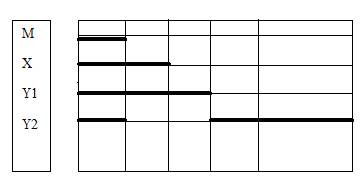
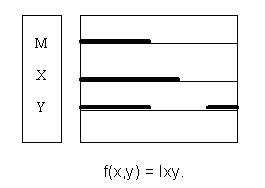
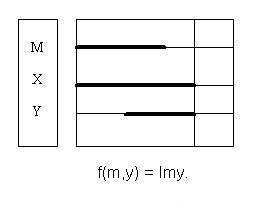
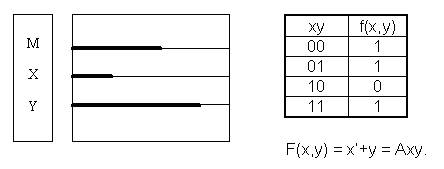
2.Занести в таблицу истинности все значения f(x,y) для входных наборов xy: 00,01,10,11.

3.Выполнить минимизацию логической функции заключения f(x,y).

4.Полученный результат представить в виде силлогистического функтора.

В случае получения многовариантного заключения можно ограничиться выполнением лишь п.1 алгоритма «ТВАТ».

Проиллюстрируем возможности Русской логики на конкретном примере. Бертран Рассел в своей работе «История западной философии» (М.:2000 –768с.) на стр.194 приводит силлогизм:

Все люди разумны.

Некоторые животные – люди.

Некоторые животные – разумны.

Покажем на этом примере недостатки мышления Б.Рассела. Во-первых, отсутствие дисциплины мышления проявляется в отсутствии универсума, хотя даже 100 лет назад Льюис Кэрролл не позволял себе такого невежества. Определим, например, в качестве универсума для силлогизма Рассела весь животный и растительный мир. Во-вторых, последняя посылка с позиции русской логики просто бестолкова. Дело в том, что частноутвердительный функтор обладает симметрией. Мы можем высказать четыре равноценных суждения:

1. Некоторые студенты - молодые люди.

2. Некоторые студенты – немолодые люди.

3. Некоторые молодые люди – студенты.

4. Некоторые немолодые люди – студенты.

В силу симметрии частноутвердительного функтора мы должны при выбранном нами универсуме считать, что некоторые люди – животные, а остальные - деревья, кусты, грибы, цветы или другие растения. В соответствии с Русской логикой и здравым смыслом вторую посылку необходимо заменить суждением «Все люди – животные», поскольку именно это утверждение соответствует истине. В-третьих, по теории великого русского физиолога И.П. Павлова, а Рассел придерживался именно этой господствующей до сих пор теории, разумными могут быть люди и только люди, т.е. «люди» и «разумные существа» – равнозначные понятия. Следовательно, и первая посылка некорректна. Устранив ошибки невежества и бестолковости Б.Рассела, получим следующие посылки.

Все люди(m) и только люди разумны(x).

Все люди(m) – животные(y).

F(x,y) =?

Решение.

Пусть x – разумные существа, m – люди, y – животные. Универсум – животный и растительный мир. Представим полную единицу системы М в виде произведения исходных посылок:

M = (x~m)Amy = (xm+x’m’)(m’+y) = m’x’+xmy+x’m’y = m’x’+xmy

F(x,y) = M(x,y) = x’+y = Axy.

Этот результат получен аналитически простым удалением аргумента m из М. Более надёжным является графическое решение.

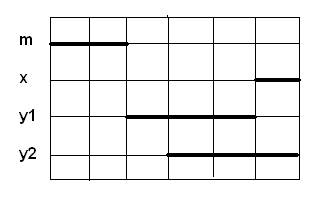
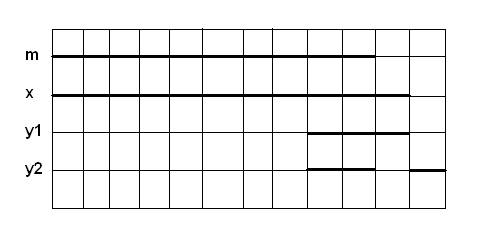
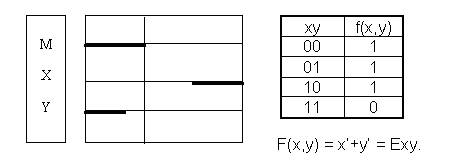
Из диаграмм Лобанова видно, что для аргументов х и y существуют следующие наборы: 00, 01 и 11. Поэтому против них в таблице истинности в графе f(x,y) записаны единицы. Набора 10 не существует, поэтому против него в графе f(x,y) записан нуль.

Таким образом мы получили правильное заключение «Все разумные – животные», что вполне согласуется со здравым смыслом и математикой. Б.Рассел в монографии «Искусство мыслить» (М.:1999) на с. 38 приводит такой силлогизм: «Если А находится вне В и В находится вне С, то А находится вне С». Данный силлогизм – образец безграмотности и глупости. По алгоритму ТВАТ построим диаграммы.

В результате мы получили трёхвариантное заключение: Aca, Iac, Eac. Кстати, если мы зададим количественные характеристики терминов: U=10, A=4, B=4, C=3, то получим двухвариантное заключение. Здесь не будет места для Eac: будут лишь Aca и Iac. Рассмотренные примеры демонстрируют не только дремучее невежество и вопиющую безграмотность Б.Рассела, но и его бестолковость.

При решении второй задачи Б.Рассела в классической логике мы получили бы так называемое интегрированное (обобщённое) заключение Iac. В настоящее время такие заключения никого не интересуют. Нам нужно знать абсолютно точно все варианты полученного решения и вероятности этих вариантов. В данном примере получены 3 варианта решения силлогизма: Eac, Aca, Iac. Это самое важное: найти все варианты заключений. Поиск вероятностей – дело техники, т.е. для средней школы дело второстепенное и необязательное. Кроме того, для определения вероятностей нужно иметь количественные характеристики всех терминов. Если в силлогизме получается лишь единственный вариант заключения, количественные характеристики терминов не нужны.

Приведём пример задачи на поиск заключения в силлогизме с заданными количественными характеристиками.

 

Задача 3.1.

В кафе оказались вместе 5 юношей. Один из них спортсмен, два отличника, два школьника и 3 студента. Известно, что спортсмен является студентом отличником и что все спортсмены - студенты.

Найти все варианты заключения.

 

Решение.

Пусть U=5 – кол-во юношей, M=1 – кол-во спортсменов, X=2 – кол-во отличников, Y=3 – кол-во студентов.

Краткая запись условия задачи выглядит так: AmxAmy.

 

 

Из скалярных диаграмм видно, что либо все отличники – студенты, либо один школьник и один студент оказались отличниками.

Более основательную информацию по силлогистике и Русской вероятностной логике можно получить из [5 - 10].

 

Практикум по силлогистике.

Большинство задач позаимствовано из книги Кэрролла (Кэрролл Л. История с узелками. - М.:Мир,1973). Для английского логика характерен дурной тон в постановке исходных посылок: иногда весьма трудно понять, что подразумевает автор под той или иной фразой. Поэтому учащийся имеет право на подсказку-перевод с невразумительного языка логика-сказочника на чёткий математический язык.

 

Задача 3.1.1.

Проверить корректность 1-го правила посылок классической силлогистики. Решение.

Это правило формулируется так: «Хотя бы одна из посылок должна быть утвердительным суждением. Из двух отрицательных посылок заключение с необходимостью не следует». Подберём контр-пример на 1-е правило посылок.

Ни один человек(m) не является бессмертным(x).

Ни один человек(m) не является счастливым(y).

F(x,y) =?

В данном силлогизме универсумом(U=5) является множество существ: смертных и бессмертных богов (х). Пусть х=1. Количество счастливых (у) в нашем случае равно 3. Пусть множество смертных состоит из людей (m=2) и 3-х медведей.

Запись условия задачи: M = EmxEmy

По алгоритму ТВАТ получим графическое решение.

Мы получили двухвариантное заключение:

Бог несчастлив (счастливы только 3 медведя).

Бог счастлив (счастливы и какие-то 2 медведя из 3-х).

Мы доказали, что первое правило посылок некорректно.

 

Задача 3.1.2.

Проверить корректность 2-го правила посылок классической силлогистики.

Решение.

Это правило формулируется так: «Если одна из посылок – отрицательное суждение, то и заключение должно быть отрицательным». Контр-пример для этого случая может быть таким.

Все люди(m) – животные(x).

Ни один человек(m) не имеет хвоста(y).

F(x,y) =?

В качестве универсума(U) примем множество животных. Наиболее наглядным является графическое решение по алгоритму ТВАТ. В этом случае можно не задавать количественные характеристики.

Аналитическая запись условия задачи выглядит так:

M = AmxEmy.

Из скалярных диаграмм видно, что заключение является общеутвердительным: «Все хвостатые существа – животные», что опровергает 2-е правило посылок.

 

Задача 3.1.3.

Проверить корректность 3-го правила посылок классической силлогистики.

Решение.

Это правило формулируется так: «Хотя бы одна из посылок должна быть общим суждением. Из двух частных посылок заключение с необходимостью не следует». Рассмотрим контр-пример:

Некоторые люди (m) неграмотны (x).

Некоторые люди (m) бескультурны (y).

F(x,y) =?

Пусть (U=6) – множество животных, люди (m=3) – часть животного мира. Предположим, что бескультурным (у=3) может быть как неграмотный (х=2), так и грамотный. Животные, кроме людей, по определению не могут быть культурными.

Вновь воспользуемся алгоритмом ТВАТ.

Краткая запись условия задачи: M = ImxImy.

Получено трёхвариантное заключение:

1. Все неграмотные культурны.

2. Все неграмотные бескультурны.

3. Некоторые неграмотные культурны.

Такое заключение перечёркивает 3-е правило посылок.

 

Задача 3.1.4.

Проверим 4-е правило посылок: если одна из посылок – частное суждение, то и заключение должно быть частным. Проведём синтез силлогизма:

Все люди (m) смертны (x)

Некоторые люди (m) неграмотны (y)

------------------------------------------------

f(x,y) =?

Решение.

Пусть в универсум входят люди, животные и боги. В этой задаче не требуются количественные характеристики. Богов будем считать грамотными.

Краткая запись условия задачи: M = AmxImy.

 

Полученный результат «Все неграмотные смертны» опровергает 4-е правило посылок.

Задача 3.1.5.

Все люди(x) смертны(m)

Сократ(y) – смертен(m)

f(x,y) =?

Решение.

Если в силлогизме в качестве универсума примем множество животных, т. е. только смертных, то, не зная, что Сократ – человек, получим следующее решение. В данном случае задание количественных характеристик не обязательно.

Краткая запись условия задачи: M = AxmAym.

Расшифровывается эта формула так: «Сократ либо человек, либо животное».

Задача 3.1.6.

Все квадраты(m) суть прямоугольники(x)

Все квадраты(m) суть ромбы(y)

f(x,y) =?

Решение.

Краткая запись условия задачи: M = AmxAmy.

Если в качестве универсума используем понятие “параллелограммы”, то получим по алгоритму ТВАТ следующий результат:

Заключение в этом случае звучит так: «Некоторые прямоугольники суть ромбы».

Задача 3.1.7.

Найти недостающую посылку:

Все люди (m) смертны (x)

f(m,y) =?

------------------------------------------------

Все неграмотные (y) смертны (х)

Решение.

Пусть в универсум входят люди, животные и боги, т.е. существа. Богов будем считать грамотными. Поскольку под грамотностью мы понимаем умение читать и писать, то всех животных необходимо признать неграмотными по определению. А поскольку нам известно, что и не все люди грамотные, то количественные параметры терминов нам не нужны. Однако за счёт подбора параметров можно получить искомую посылку в виде Emy.

Краткая запись условия задачи выглядит так:

Amx & f(m,y) → Ayx.

Изобразив на диаграммах Лобанова исходную посылку и заключение, легко найдём недостающую посылку:

Полученная посылка «Некоторые люди неграмотны» в очередной раз опровергает одно из классических правил посылок.

Задача 3.1.9.

Только философы (x) эгоисты (m).

Нет циника (y), который не был бы эгоистом (m).

-----------------------------------------------------------

Следовательно, все циники – философы.

Решение.

Пусть x – философы, y – циники, m – эгоисты. Универсум – люди. Краткая запись условия задачи выглядит так: Amx & Aym → f(x,y). Количественные характеристики не требуются.

Тогда по алгоритму ТВАТ получим:

Заключение: «Все циники – философы».

Задача 3.1.10.

Каждого, кто верит в себя, можно считать Человеком.

Никто, ни один Человек не верит политикам.

----------------------------------------------------------------------------

Все, кто верит политикам, не верит в себя.

Решение.

Пусть х – кто верит в себя, m – Человек, у – кто верит политикам. Универсум – люди. Условие задачи: (x ~ m) & Eym → f(x,y).

Задача 3.1.11.

Нет таких членов парламента, которые не участвуют в законотворчестве.

Только 20% членов парламента составляют юристы.

-----------------------------------------------------------------------------------------------

Не все, кто создают законы, являются юристами.

Решение.

В этом силлогизме Кэрролла следует задать количественные характеристики. Пусть m=10 – к-во членов парламента (тогда число парламентариев-юристов равно 2), x=11 – число законотворцев, y=3 - число юристов, U=12 – кол-во людей в зале заседаний.

Условие задачи: Amx & Iym → f(x,y).

Получено 2-вариантное заключение:

1. Все юристы – законотворцы (Ayx).

2. Все неюристы – законотворцы и все незаконотворцы – юристы (Ay’xAx’y).

Задача 3.1.12.

Среди юристов имеются профессиональные бизнесмены.

Настоящий бизнесмен не боится инфляции.

__________________________________________

Некоторые юристы не опасаются инфляции.

Решение.

Здесь Кэрролл, как всегда, некорректен: он не задал количественные характеристики. Пусть x=4 – юристы, m=4 – бизнесмены, y=6 – не боящиеся инфляции предприниматели. Универсум U=8 – группа людей.

Условие задачи: Imx & Amy → f(x,y).

Получено 2-вариантное заключение:

1. Все юристы не боятся инфляции (Aхy).

2. Все неюристы не боятся инфляции и все не боящиеся инфляции предприниматели – юристы (Ax’yAy’x).

Задача 3.1.13.

Не всякий любитель насилия любит собственных детей.

Только политики верят в пользу насилия.

----------------------------------------------------------------------------------

Некоторые политики не любят своих детей.

Решение.

Пусть x=4 – политики, m=4 – любители насилия, y=6 – не любящие своих детей родители. Универсум U=8 – группа людей. Условие задачи: Imx & Amy → f(x,y).

 

Получено 3-вариантное заключение:

1. Все политики не любят своих детей (Aхy).

2. Все неполитики не любят своих детей и все любящие своих детей родители – политики (Ax’yAy’x).

3. Некоторые политики не любят своих детей (Iхy).

 

Задача 3.1.14.

Только в споре рождается истина.

Никто не станет спорить, кроме глупца или мошенника.

-------------------------------------------------------------------------------

Лишь глупец или мошенник могут достичь истины.

Решение.

Пусть x – “родители истины”, m – спорщики, y – глупец или мошенник. Универсум – люди.

Условие задачи: Axm & Amy → f(x,y).

Полученное заключение: «Родители истины» - глупцы или мошенники.

Задача 3.1.15.

Боязливый к прекрасному полу – боязлив и в жизни.

Тот, кто знает логику, не боится женщин.

----------------------------------------------------------

Трус не разбирается в логике.

Решение.

Пусть x=6 – боязливый в жизни, m=4 – боящийся женщин, y=2 – знающий логику. Универсум U=8 – группа мужчин.

Условие задачи: Amх & Еmy → f(x,y).

Получено 3-вариантное заключение:

1. Ни один трус не знает логику (Exy).

2. Все логики – трусы (Ayx).

3. Некоторые логики – трусы (Ixy).

В данном случае исходное заключение Кэрролла кардинально ошибочно.

 

Задача 3.1.16.

Среди болтунов нет логиков.

Все политики - болтуны.

-------------------------------------------------------

Ни один логик не станет политиком.

Решение.

Пусть x – логик, m – болтун, y – политик. Универсум – люди.

Условие задачи: Emх & Aym → f(x,y).

Ни один политик не является логиком.

 

Задача 3.1.17.

Иногда проходимец может оказаться ясновидцем.

Если ты ясновидец, то не должен лгать.

--------------------------------------------------------------------------------------

Существуют проходимцы, которые обязаны говорить правду.

 

Решение.

Пусть x=4 – проходимец, m=4 – ясновидец, y=6 – честный. Универсум U=8 – люди. Условие задачи: Imx & Amy → f(x,y).

 

Получено 3-вариантное заключение:

1. Все проходимцы – честные (Aхy).

2. Все непроходимцы – честные и все нечестные – проходимцы (Ax’yAy’x).

3. Некоторые проходимцы – честные (Iхy).

 

Задача 3.1.18.

Все лентяи – двоечники.

Ни один студент не любит получать двойки.

---------------------------------------------------------------

Значит, среди студентов нет лентяев.

Решение.

Пусть x – лентяй, m – двоечник, y – студент.Универсум – учащиеся.

Условие задачи: Axm & Emy → f(x,y).

Заключение: «Ни один студент не является лентяем.

 

ЛОБАНОВ ВЛАДИМИР ИВАНОВИЧ

 

 

АВТОБИОГРАФИЯ.

Родился 1 марта 1940г. в г. Осташкове Калининской обл. на берегу оз. Селигер. Отец, Лобанов Иван Ефимович, инженер, нач. Осташковского радиоузла, погиб на фронте в мае 1942г. Мать, Лобанова Ольга Сергеевна, до войны сотрудница оборонного института, после войны няня в детских яслях. После эвакуации с 1941г. по 1946г. проживал в г.Суздаль.

В 1947г поступил в среднюю школу №63 г. Осташкова. Был отличником, пионером, комсомольцем. В 1957г. поступил в Осташковский механический техникум (ОМТ).

В 1960г. окончил теплотехническое отделение ОМТ. Диплом с отличием. Работал теплотехником (г. Сталинабад). 1960 – 1963 гг. – служба в Советской Армии (группа глубинной разведки, спецназ, в/ч 77701, г. Ош, ТуркВО). Был отличником Советской Армии, старшим разведчиком. Горжусь службой в спецназе. В армии был принят кандидатом в члены КПСС.

В 1963г. поступил в Ивановский энергетический институт (ИЭИ). В 1964г. принят в члены КПСС. Занимался спортом – имел разряды по лыжам, лёгкой атлетике, волейболу, ручному мячу, военному троеборью, фигурному катанию (парное и спортивные танцы на льду). Был солистом танцевальных ансамблей ИДНТ и ИЭИ. Окончил ИЭИ в 1968г по специальности инженер по автоматизации теплоэнергетических процессов. Ленинский стипендиат, диплом с отличием. Работал старшим инженером-наладчиком в тресте ОРГРЭС (г. Горловка). Налаживал автоматику горения энергоблоков 300МВт на Новочеркасской ГРЭС. Возглавлял бригаду специалистов по наладке автоматики ТЭЦ ВАЗ (г. Тольятти).

С 1972 по 1973 гг. обучение в аспирантуре ВТИ им. Дзержинского(г. Москва). Сдал все экзамены кандидатского минимума, но работа над диссертацией показалась бесперспективной.

1973 - 1979 гг. работал ведущим инженером НИИРТА (НПО «Импульс») по созданию систем управления оборонного назначения.

С 1979г. по 1995г. возглавлял отдел 450 ЦНИИ "Циклон", головной институт МЭП СССР. Внедрение микроэлектроники и вычислительной техники в народное хозяйство. Защитил кандидатскую диссертацию. Имею более 90 научных публикаций. В 2001г. издал книгу "Азбука разработчика цифровых устройств", в которой значительно расширил методологию цифровых разработок, а также решил проблему создания логики здравого смысла, т.е. Русской логики. В 2002г. издал книги «Русская логика против классической» и «Решебник по Русской логике». Впервые в мире решены проблемы Лейбница и при этом были доказаны некорректность и неполнота силлогистики Аристотеля, а также подвергнуто критике кванторное исчисление, т.е. дана отрицательная оценка мировой математической науки в области теории множеств и предложены пути преодоления указанных недостатков. Результаты по Русской логике были доложены на общероссийских и международных конференциях в Москве и Санкт-Петербурге (СпбГУ) в 1998-2000гг, а также в ИЕН РАН и на конференции «Эволюция и иносферы» в Президиуме РАН(28.03.2001). Мною прочитаны курсы лекций по русской логике во Всероссийском обществе «Знание»(1999-2000гг.), а также в ТВАТ(1995-2001гг.) и других лицеях, колледжах и вузах. Все мои работы по Русской логике, т.е. фактически по алгебре множеств, за 1998 – 1999гг. переведены в США. В течение 2004 - 2009 гг. издал книги «Русская логика для школьников (и академиков), «Русская логика для «физиков» и «лириков», «Русская логика для школьников и умных академиков», «Русская вероятностная логика». Было доказано, что не существует кванторного исчисления, что алгебра множеств и алгебра логики – синонимы, что нет логики предикатов, что вся логика вероятностна. Были обнаружены и устранены ошибки П.С.Порецкого в методике решения логических уравнений. Лекции по Русской логике транслировались по спутниковому телевидению на канале СГУ-ТВ.

С 1995 по 1998гг. возглавлял (по конкурсу) отдел автоматики в фирме "РоссЭко". За время работы в НИИРТА создал в рамках ОКР несколько приборов для систем бортового управления, доведя их до выпуска опытных партий (в их числе пр.20 изделия 83В6 и др.). Проводил обучение ведущих специалистов НИИРТА инженерным методам разработки цифровых устройств.

В ЦНИИ "Циклон" мною лично или под моим руководством были разработаны в результате проведения НИОКР следующие устройства и системы: УУ УКВ-тюнером, УУ всеволновым тюнером (на КР 580ИК80),система автоконтроля таксофонов(на КР1801ВЕ1), микроконтроллерный регулятор(на i8048)-прообраз ПРОТАРа МЗТА, отладочное устройство "Техника" для TMS270, оригинальные запатентованные адаптируемые отладочные системы АОС-6502, АОС-1814, АОС-1868, АОС-1801; автоматизированная система централизованной охраны и обороны ОНХ и квартир граждан, диагностический процессор, инструментальные системы контроля и диагностики цифровых устройств.

Работал на нескольких десятках микропроцессоров и микро-ЭВМ. Владею несколькими языками программирования высокого уровня(ALGOL,FORTRAN,FORTH,PASCAL,MODULA,C,РАЯ) и многими ассемблерами. Программист высокой квалификации. Работал на нескольких типах ЭВМ и ПК.

С 13.10.1998г. по 31.01.2000г. работал в НПО «Химавтоматика» в должности главного специалиста по микроэлектронике. Разрабатывал микроконтроллеры для газовых анализаторов. С 7.02.2000г. по 12.05.2001 работал в ОАО «Импульс» над созданием систем управления оборонного назначения (КПА-БАНКОР, БСК-Контейнер, КПА-БСК). С 22.05.2001 по 12.12.2003 работал главным специалистом на НПП «Редан» (ГНПП «Регион», Каширское ш., 13а) по разработке цифровых систем управления оборонного назначения. С 15.01.2004 по 31.12.2006 работал гл.специалистом на НПП «НИИДАР». Разрабатывал схемы цифрового телевидения. С 9.03.2007 по настоящее время работаю ведущим научным сотрудником в ФГУП «ЦНИИ «Комета» по разработке электронных устройств оборонного назначения.

Являюсь изобретателем, трижды лауреатом премии ВДНХ, награжден медалью "Ветеран труда".

 

Литература.

1. Сайты в Internet: http://logicrus.ru, http://ruslogic.narod.ru, http://matema.narod.ru/newpage113.htm, http://www.mirit.narod.ru/zerkalo.htm, http://ito.edu.ru/, http://www.trinitas.ru, http://lord-n.narod.ru/walla.html/Книги и софт с Walla.com, http://naztech.org/lobanov, http://www.rsl.ru и др.

2. Лобанов В.И.. Инженерные методы разработки цифровых устройств. - М:НИИРТА, 1977(шифр Центр. Политехн. Библиотеки - W145 4/231)(шифр библ. НИИРТА –-507/Л68).

3. Лобанов В.И. Азбука разработчика цифровых устройств. – М.: Горячая линия – Телеком, 2001 – 192с.

4. Лобанов В.И. Русская логика против классической (азбука математический логики). – М.: Компания Спутник+, 2002 – 126с.

5. Лобанов В.И. Решебник по Русской логике. – М.: Компания Спутник+, 2002 – 133с.

6. Лобанов В.И. Русская логика для школьников (и академиков). – М.: Издательство «Эндемик», 2004 – 110с.

7. Лобанов В.И. Русская логика для «физиков» и «лириков». – М.: Спутник+, 2005 – 427с.

8. Лобанов В.И. Курс лекций «Математика в логике» для спутникового образовательного телевидения. – М.: СГА, Спутниковое телевидение, канал СГУ-ТВ – телестудия Современной Гуманитарной Академии, 2007.

9. Лобанов В.И. Русская вероятностная логика для школьников и умных академиков. – М.: 2008 – 33с.

10. Лобанов В.И. Русская вероятностная логика. – М.: «Русская Правда», 2009 – 320с.

11. Порецкий П.С. О способах решения логических равенств и об одном обратном способе математической логики. - Казань:1884.

12. Смаллиан Р.М. Как же называется эта книга? – М.: 2008 – 272 с.

 

Оглавление.

Русская логика в информатике (Букварь математической логики). 1

Предисловие. 1

1. Алгебра логики. 4

1.1 Основные положения алгебры логики. 4

1.2 Основные законы алгебры Буля. 5

1.3. Синтез логических функций. 8

1.4.Минимизация полностью определённых булевых функций. 9

1.5. Минимизация недоопределённых булевых функций. 13

1.6. Практикум по синтезу и минимизации логических функций. 15

2. Законы логики суждений. 18

2.1. Практикум по логике суждений. 21

3. Силлогистика. 25

Алгоритм «ТВАТ» (графический синтез силлогизмов) 27

3.1. Практикум по силлогистике. 31

ЛОБАНОВ ВЛАДИМИР ИВАНОВИЧ.. 42

Литература. 45

Оглавление. 46

 

 

Русская логика в информатике (Букварь математической логики).

Аннотация

Данная брошюра в популярной форме знакомит читателей с наиболее значимыми разделами Русской логики, которая опровергает многие постулаты классической логики, являясь на сегодня единственной истинно математической логикой. Автор обвиняет современных матлогиков в невежестве и безграмотности. Брошюра рассчитана на школьных преподавателей мат