Основные законы алгебры Буля.

 

Прежде, чем приступить к изложению основных законов алгебры логики, зафиксируем некоторые очевидные её положения.

1 + a = 1; 0 + a = a; a & 1 = a; a & 0 = 0; a + a’ = 1.

Эти соотношения легко проверяются по таблице истинности для логической функции ИЛИ подстановкой 0 или 1 вместо аргумента a.

 

 

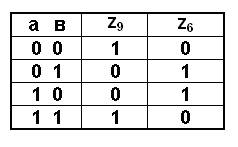
В булевой алгебре все операции осуществляются с логическими переменными и подчиняются законам алгебры логики. Опишем и докажем некоторые из них.

а) Переместительный закон

а + в = в + а; ав = ва

б) Сочетательный закон

(а + в) + с = а + (в + с); (ав)с = а(вс)

в) Распределительный закон

а(в + с) = ав + ас; а + вс = (а + в)(а+с)

г) Закон поглощения

а + ав = а(1 + в) = а; а(а + в) = а + ав = а

д) Закон склеивания

ав + ав’ = а(в + в’) = a & 1 = a; (а + в)(а + в’) = а

е) Идемпотентный закон

a + a = a; a & a = a

Вышеприведённые законы легко проверяются подстановкой 0 и 1 вместо аргументов a, b, c.

ё) Правила де Моргана

Эти правила справедливы для любого числа аргументов.

а + в + с +.... + z = (а’в’с’...z’)’

авс... = (а’ + в’ + с’ +... + z’)’

Правила можно описать таким алгоритмом.

Для перехода от логической суммы к логическому произведению необходимо проделать следующие операции:

1) проинвертировать все слагаемые в отдельности;

2) заменить знаки сложения знаками умножения;

3) проинвертировать получившееся выражение.

Аналогично выполняется переход от логического произведения к логической сумме. В инженерной практике используются лишь правила де Моргана и закон склеивания.

Кроме основных функций И(f₁), ИЛИ(f₂), НЕ(f₃), в алгебре логики часто используются функции равнозначности (эквивалентности) и неравнозначности (сумма по модулю 2). Для обозначения этих функций применяют следующие символы: равнозначность - ~ и =, сумма по модулю 2 - Å и ≠. Содержание этих функций отражено в таблице.

Смысл этой таблицы прост: если a = b, то функция равнозначности z₉ = 1. Если же a ¹ b, то z₉ = 0, а функция неравнозначности z₆ = 1. Для того, чтобы по таблице истинности построить булеву функцию, достаточно выписать все наборы входных переменных и представить их в виде логической суммы. Если какая-либо переменная входит в набор нулём, то она в символьном виде отображается своей инверсией.

Из таблицы получаем:

z₉ = а ~ в = 00 + 11 = а’в’ + ав – равнозначность;

z₆ = a Å в = 01 + 10 = а’в + ав’ – сумма по модулю 2, или неравнозначность.

Из таблицы видно, что

z₉ = z₆’ или z₉’ = z₆.

Таким образом,

а’в’ + ав = (ав’ + а’в)’, или

а~в = (а Å в)’, а Å в = (а~в)’.

 

Особое место в алгебре логики занимает функция импликации: a→b = a’+b. Переводится приведённая формула импликации на русский язык так: если истинно a, то b тоже истинно. Например, пусть a – я выучу все энциклопедии, а b – обыграю всех телезнатоков. Тогда запись a→b будет означать следующее суждение: если я выучу все энциклопедии, то обыграю всех телезнатоков.

Все вышеприведённые правила и законы даны не для запоминания-зубрёжки, а в качестве справочного материала. Нужно никогда не забывать, что главным инструментом является Ваша светлая голова, Ваше мышление.

 

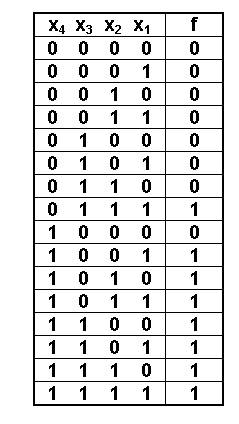
Синтез логических функций

Под синтезом логических функций будем понимать процесс её получения по словесному описанию, по таблице истинности или любому другому способу задания этой функции. Синтез логических функций можно проиллюстрировать решением простой задачи.

Задача 1.1.

Приёмная комиссия в составе трех членов комиссии и одного председателя решает судьбу абитуриента большинством голосов. В случае равного распределения голосов большинство определяется голосом председателя. Найти краткое определение ситуации, в которой абитуриент будет принят в учебное заведение. Найти решение в виде логической функции, т.е. построить автомат для тайного голосования.

Решение.

Пусть f - функция большинства голосов. f = 1, если большинство членов комиссии проголосовало за приём абитуриента, и f = 0 в противном случае.

Обозначим через x₄ голос председателя комиссии. x₄ = 1, если председатель комиссии проголосовал за приём абитуриента. x₃, x₂, x₁ - голоса членов приёмной комиссии.

С учётом вышеуказанных допущений условие задачи можно однозначно представить в виде таблицы истинности.

Заполнение таблицы осуществляем с учётом того, что функция f является полностью определённой, т.е. она определена на всех возможных наборах переменных x₁ - x₄. Для n входных переменных существует N = 2ⁿ наборов переменных. В нашем примере N = 2⁴ = 16 наборов.

Записывать эти наборы можно в любом порядке, но лучше в порядке возрастания двоичного кода.

Примечание. Здесь и далее под набором будем понимать конъюнкцию, т.е. логическое произведение, всех входных переменных.

Все наборы, на которых функция принимает значение 1, будем называть единичными, или рабочими. Наборы, на которых функция принимает значение 0, будем называть нулевыми, или запрещенными (по Мавренкову Л.Т.).

Для того, чтобы по таблице истинности найти функцию f, достаточно выписать все единичные наборы и соединить их знаком дизъюнкции.

 

Таким образом,

f = 0111+1001+1010+1011+1100+1101+1110+1111

или в символьном виде

f = x₄’x₃x₂x₁+x₄x₃’x₂’x₁+x₄x₃’x₂x₁’+x₄x₃’x₂x₁+x₄x₃x₂’x₁’+x₄x₃x₂’x₁+

+x₄x₃x₂x₁’+x₄x₃x₂x₁

Полученная форма функции называется совершенной дизъюнктивной нормальной формой (СДНФ), здесь каждое логическое слагаемое представляет собой конъюнкцию всех аргументов. В случае, когда не каждое слагаемое представляет собой конъюнкцию всех аргументов, то такая форма представления логической функции называется просто ДНФ. Очевидно, применяя основные законы булевой алгебры, мы могли бы аналитически уменьшить сложность полученного выражения. Но это наихудший способ минимизации булевых функций.