
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Суммы Дарбу и интегрируемость функции по Риману.
Теорема: Функция Доказательство:
Докажем необходимость условия: Функция Пусть
т.е. Далее имеем: Необходимость доказана.
Докажем достаточность условия:
Докажем, что
Достаточность доказана. Билет 41 Основная теорема о существовании определенного интеграла Римана. Теорема (Основная) Ограниченная функция f интегрируема на отрезке [a,b] тогда и только тогда, когда Доказательство:
Σ1: Σ2: разобъем Σ2 на повторные суммы, т.е. Σ2=Σ(Σ i). Σ i≤
Следствие 1: Функция f – интегрируема на [a,b], если Следствие 2: Функция f – интегрируема на [a,b], если
Билет 42 Равномерная непрерывность функции. Модуль непрерывности. Определение 1: Определение 2(Критерий Коши): Теорема 1 (Эквивалентность определений 1 и 2) Доказательство: Так как Теорема 2 Функция непрерывная на отрезке, равномерно непрерывна на нем ( Доказательство: Допустим что теорема неверна. Построим отрицание к определению 2.
Необходимость условия: Если Пример Билет 43
|
|||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 397; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.147.53 (0.008 с.) |
 интегрируема на отрезке
интегрируема на отрезке  тогда и только тогда, когда
тогда и только тогда, когда  .
.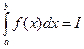 , тогда
, тогда 

 , т.е.
, т.е.  .
.
 и
и  .
.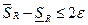 , т.е.
, т.е.  .
. .
. .
.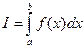 .
.
 ,
,
 ,
, , тогда
, тогда  , т.е.
, т.е.  ,
, .
. .
. По теореме об интегрируемости (f интегрируема Û
По теореме об интегрируемости (f интегрируема Û  ) функция интегрируема тогда и только тогда, когда
) функция интегрируема тогда и только тогда, когда 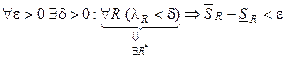 (1). Надо доказать, что если
(1). Надо доказать, что если  . Т.е. если найдется одно R*, удовлетворяющее неравенству (1), то оно (неравенство) будет выполняться для всех R. Возьмем произвольное
. Т.е. если найдется одно R*, удовлетворяющее неравенству (1), то оно (неравенство) будет выполняться для всех R. Возьмем произвольное  . Нужно найти δ, такое чтобы выполнялось неравенство
. Нужно найти δ, такое чтобы выполнялось неравенство 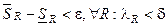 . По условию теоремы
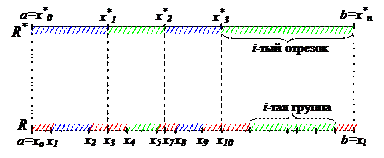
. По условию теоремы  . Рассмотрим наше разбиение R* и произвольное R, как показано на рисунке. Составим разность верхней и нижней сумм Дарбý для нового разбиения R:
. Рассмотрим наше разбиение R* и произвольное R, как показано на рисунке. Составим разность верхней и нижней сумм Дарбý для нового разбиения R:  . Нужно сделать его меньше
. Нужно сделать его меньше  . Обозначим через Σ первую сумму и разобъем ее: Σ=Σ1+Σ2. Σ1 – такие слагаемые, что элемент нового разбиения R содержит в себе хотя бы одну точку границы старого раазбиения R*. Все остальное войдет в Σ2. Рассмотрим отдельно Σ1 и Σ2:
. Обозначим через Σ первую сумму и разобъем ее: Σ=Σ1+Σ2. Σ1 – такие слагаемые, что элемент нового разбиения R содержит в себе хотя бы одну точку границы старого раазбиения R*. Все остальное войдет в Σ2. Рассмотрим отдельно Σ1 и Σ2: т.к. функция f – ограничена (k - константа). Тогда
т.к. функция f – ограничена (k - константа). Тогда  (M и m – максимум и минимум на [a,b]). Получим Σ1
(M и m – максимум и минимум на [a,b]). Получим Σ1  , где λR<δ, а количество красных отрезков не превосходит 2n. Для того чтобы это неравенство выполнялось, достаточно взять δ<
, где λR<δ, а количество красных отрезков не превосходит 2n. Для того чтобы это неравенство выполнялось, достаточно взять δ<  ≤
≤  (Mi*-mi*) ΣΔ xi*, где Mj и mj – максимум и минимум на j -том участке. Σ i – группировка тех новых j -тых участков, которые попали в один и тот же старый. Получим Σ2
(Mi*-mi*) ΣΔ xi*, где Mj и mj – максимум и минимум на j -том участке. Σ i – группировка тех новых j -тых участков, которые попали в один и тот же старый. Получим Σ2  ÞΣ1+Σ2 <ε, т.е. Σ <
ÞΣ1+Σ2 <ε, т.е. Σ <  . Теорема доказана.
. Теорема доказана. с
с  :
:  (если существует такая последовательность разбиений с мелкостью, стремящейся к нулю, что модуль разности последовательности интегральных сумм и интеграла стремится к нулю).
(если существует такая последовательность разбиений с мелкостью, стремящейся к нулю, что модуль разности последовательности интегральных сумм и интеграла стремится к нулю). (если верхний интеграл равен нижнему).
(если верхний интеграл равен нижнему). ограниченная
ограниченная  и
и  при выполнении условия
при выполнении условия  ,
,  называется равномерно непрерывной.
называется равномерно непрерывной. при
при  ).
). . Зададим стремящуюся к нулю последовательность положительных чисел
. Зададим стремящуюся к нулю последовательность положительных чисел  , тогда
, тогда  . Так как точки последовательности
. Так как точки последовательности  принадлежат к отрезку
принадлежат к отрезку  , сходящуюся к некоторой точке
, сходящуюся к некоторой точке  . Значит, из нее можно выделить также подпоследовательность
. Значит, из нее можно выделить также подпоследовательность 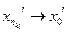 . Аналогично выделим подпоследовательность
. Аналогично выделим подпоследовательность 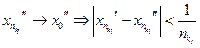 и
и 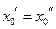
 . Получили противоречие – теорема доказана.
. Получили противоречие – теорема доказана. , то теорема 2 не выполняется.
, то теорема 2 не выполняется. Пусть
Пусть  при
при  .
.


