
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неравенства для определенного интеграла Римана и теорема о среднем. ⇐ ПредыдущаяСтр 6 из 6
Теорема 1: Если функции Доказательство:
Следствие: Если Доказательство: Известно неравенство:
Теорема 2: (о среднем) Пусть
и Замечание: sup и inf существуют, т.к. функция на данном промежутке интегрируема, а значит ограничена. Доказательство: Запишем неравенство:
Если Если
Следствие: Если Доказательство: Т.к. Следствие к следствию: Если Доказательство: Возьмем
Если считать площадь криволинейной трапеции, то найдется такая точка
Билет 47 Интеграл как функция верхнего предела. Непрерывность и дифференцируемость. Теорема Ньютона-Лейбница.
Рассмотрим функцию
Теорема: Если функция
Доказательство: Рассмотрим функцию
Теорема доказана.
Теорема: Пусть функция
Доказательство:
Теорема доказана.
Следствие: Если функция
Функция Т.е. любая непрерывная функция имеет первообразную. Теорема доказана.
Формула Ньютона-Лейбница: Функция Доказательство: Функция
Билет 48
|
|||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 203; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.196.27 (0.008 с.) |
 интегрируемы на
интегрируемы на  и
и 

 выполняется неравенство
выполняется неравенство  , тогда
, тогда  . Так как интегралы по условию существуют, по теореме о предельном переходе под знаком неравенства,
. Так как интегралы по условию существуют, по теореме о предельном переходе под знаком неравенства,  . Теорема доказана.
. Теорема доказана. - интегрируема на
- интегрируема на  - интегрируем на данном отрезке; тогда
- интегрируем на данном отрезке; тогда 
 ; по данной теореме
; по данной теореме ; из самого правого интеграла минус можно вынести; получим:
; из самого правого интеграла минус можно вынести; получим: интегрируемы на
интегрируемы на  на данном промежутке, тогда
на данном промежутке, тогда , где
, где  ,
, 

 и домножим его на
и домножим его на 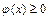 :
: ; тогда по теореме о неравенствах это неравенство сохранится и в интегралах:
; тогда по теореме о неравенствах это неравенство сохранится и в интегралах: )
) , то и интеграл
, то и интеграл  и неравенство (
и неравенство ( , тогда по теореме о неравенствах
, тогда по теореме о неравенствах  , значит можно неравенство (
, значит можно неравенство ( и принимаем за
и принимаем за  . Теорема доказана.
. Теорема доказана. непрерывна на
непрерывна на 
 - по теореме о промежуточных значениях непрерывной функции. Следствие доказано.
- по теореме о промежуточных значениях непрерывной функции. Следствие доказано.
 , тогда
, тогда  (по следствию)
(по следствию)  . Следствие доказано.
. Следствие доказано. Геометрический смысл этого следствия:
Геометрический смысл этого следствия: , что площадь этой криволинейной трапеции будет равна площади прямоугольника с высотой
, что площадь этой криволинейной трапеции будет равна площади прямоугольника с высотой  .
. , интегрируемую на отрезке
, интегрируемую на отрезке  . По аддитивному свойству интеграла:
. По аддитивному свойству интеграла: , можно найти отрезок
, можно найти отрезок  на котором представляется возможным рассмотреть функцию
на котором представляется возможным рассмотреть функцию  .
. непрерывна на отрезке
непрерывна на отрезке  ,
, , где
, где  ,
,  ,
,  , где
, где 
 , тогда функция
, тогда функция  и
и 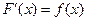 .
.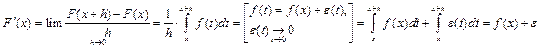 ,
, ,
, 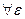

 , т.е.
, т.е. .
. , т.е.
, т.е.  - первообразная
- первообразная  ,
, .
. - её произвольная первообразная. Тогда
- её произвольная первообразная. Тогда  .
. ,
,  ,
,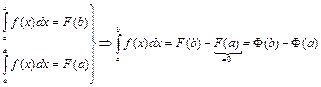 . Теорема доказана.
. Теорема доказана.


