
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегрирование тригонометрических выражений.
Пусть 1) Если один из многочленов 2) Если один из многочленов 3) Если оба многочлена четные по 3’) Выражения вида 4) Универсальная подстановка. Рационализация
5) Выражения вида
Билет 36 Тригонометрические подстановки. Следующие интегралы превращаются в тригонометрические выражения при помощи тригонометрических подстановок:
Пример:
Билет 37 Определенный интеграл Римана. Эквивалентные определения. Условие Коши. Пусть задана функция f(x) на отрезке
Это интегральная сумма, соответствующая разбиению R и выбору точек Если существует предел при
Определение по Коши:
По Гейне:
Критерий Коши:
Билет 38 Ограниченность интегрируемой функции. Теорема: Если функция f(x) интегрируема на [a,b] и существует Доказательство: От противного: пусть f(x) неограниченна на [a,b]. Введем произвольное разбиение R:
Теорема доказана.
Билет 39 Суммы Дарбу. Их Свойства. Определение:
Пусть R: Тогда можем составить выражения:
Пусть R: Тогда можем составить выражения:
Свойства сумм Дарбу: 1) 2) Рассмотрим два разбиения в случае, когда одно разбиение является продолжением другого. Т.е.
Заметим, что если
3)
=>
Билет 40
|
|||||
|
Последнее изменение этой страницы: 2017-02-09; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.114.38 (0.012 с.) |

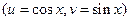 , где
, где  и
и  - многочлены от
- многочлены от  и
и 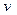 .
.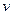 , а другой – нечетный по
, а другой – нечетный по  рационализирует интеграл.
рационализирует интеграл. , а другой – нечетный по
, а другой – нечетный по  рационализирует интеграл.
рационализирует интеграл. рационализирует интеграл.
рационализирует интеграл. , где
, где  и
и  - четные. Они сходны с 3 случаем, где
- четные. Они сходны с 3 случаем, где 
 также достигается с помощью подстановки
также достигается с помощью подстановки  , которая называется универсальной. В самом деле,
, которая называется универсальной. В самом деле, ;
;  ;
; 
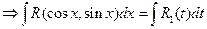 .
. ;
;  ;
;  . Они рационализируются с помощью перевода в тригонометрические суммы.
. Они рационализируются с помощью перевода в тригонометрические суммы.

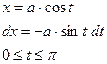

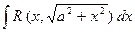
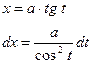





 . Составим разбиение R:
. Составим разбиение R:  .
.
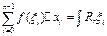
 .
. интегральных сумм
интегральных сумм  , и он не зависит от R и
, и он не зависит от R и 

 , где
, где  - последовательность разбиений.
- последовательность разбиений.

 , то функция ограничена на этом отрезке.
, то функция ограничена на этом отрезке. . Т.к. функция неограниченна на [a,b], то она неограниченна хотя бы на одном из отрезков
. Т.к. функция неограниченна на [a,b], то она неограниченна хотя бы на одном из отрезков  . Пусть
. Пусть 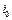 - номер того отрезка, на котором функция неограниченна. Тогда рассмотрим интегральную сумму:
- номер того отрезка, на котором функция неограниченна. Тогда рассмотрим интегральную сумму: - т.е. выделили суммы одно слагаемое. Обозначим
- т.е. выделили суммы одно слагаемое. Обозначим  , тогда получим:
, тогда получим: (следует из неравенства о модулях). Тогда возьмем произвольное N и сделаем разность
(следует из неравенства о модулях). Тогда возьмем произвольное N и сделаем разность 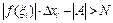 . Для этого у нас должно быть
. Для этого у нас должно быть 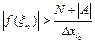 . У нас функция неограниченна на отрезке
. У нас функция неограниченна на отрезке  . Тогда интегральная сумма будет
. Тогда интегральная сумма будет  , т.е. будет являться величиной неограниченной, т.е. не будет существовать ее предела, а значит и
, т.е. будет являться величиной неограниченной, т.е. не будет существовать ее предела, а значит и  ограничена на отрезке
ограничена на отрезке  . Введём разбиение R этого отрезка.
. Введём разбиение R этого отрезка. ,
,  .
. - нижняя сумма Дарбу,
- нижняя сумма Дарбу,  - верхняя сумма Дарбу.
- верхняя сумма Дарбу. ,
,  .
. , для одного и того же разбиения.
, для одного и того же разбиения. - продолжение
- продолжение  , если все точки
, если все точки 
 Добавление точек не увеличивает
Добавление точек не увеличивает  и не уменьшает
и не уменьшает  . Пусть
. Пусть  ,
,  ,
, ,
, ,
, , то
, то  и
и  . Отсюда заключаем:
. Отсюда заключаем: ,
,  ,
,  ,
,  .
.
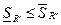 ,
,  ,
, ,
, , т.е.
, т.е.  .
.
 - нижний интеграл (нижняя точная сумма Дарбу).
- нижний интеграл (нижняя точная сумма Дарбу).  .
. - верхний интеграл (верхняя точная сумма Дарбу).
- верхний интеграл (верхняя точная сумма Дарбу).  .
. .
.


