Диаграмма Парето по причинам

Эта диаграмма отражает причины проблем, возникающих в ходе производства, и используется для выявления главной из них:

· исполнитель работы: смена, бригада, возраст, опыт работы, квалификация, индивидуальные характеристики;

· оборудование: станки, агрегаты, инструменты, оснастка, организация использования, модели, штампы;

· сырье: изготовитель, вид сырья, завод-поставщик, партия;

· метод работы: условия производства, заказы-наряды, приемы работы, последовательность операций;

· измерения: точность (указаний, чтения, приборная), верность и повторяемость (умение дать одинаковое указание в последующих измерениях одного и того же значения), стабильность (повторяемость в течение длительного периода), совместная точность, т. е. вместе с приборной точностью и тарированием прибора, тип измерительного прибора (аналоговый или цифровой).

 

Построение диаграммы Парето состоит из следующих шагов [15]:

Предполагается, что на данном этапе мы уже имеем результаты всех предыдущих шагов по решению проблем: формулировка и постановка проблемы, анализ ее, сбор необходимых данных и фиксация их в контрольных листках.

Для построения диаграммы необходимо разработать бланк таблицы, в которую заносят:

· типы (признаки) случаев, фактов (данные лучше всего располагать в убывающем порядке – в начале таблицы тип события, имеющий наибольшее количество повторений, в конце таблицы - наименьший);

· количество появлений (повторений) каждого типа;

· накопленная сумма числа каждого типа (с нарастающим итогом: к числу предыдущего типа прибавляется следующее);

· процент числа по каждому признаку в общей сумме;

· накопленный процент (с нарастающим итогом).

В таблице следует подсчитать общую сумму количества случаев по всем типам (признакам).

Далее необходимо начертить одну горизонтальную и две вертикальные оси.

1. Вертикальные оси:

· левая ось с интервалами от 0 до общей суммы количества выявленных случаев;

· правая ось с интервалами от 0 до 100.

1. Горизонтальная ось. Интервалы на ней должны быть одинаковыми и соответствовать числу типов (признаков), указанных в таблице.

Затем строится столбиковая диаграмма по значениям типов (признаков) случаев и кумулятивная кривая (кривая Парето). На вертикалях, соответствующих правым концам каждого интервала на горизонтальной оси, наносятся точки накопленных сумм (результатов или процентов) и соединяются между собой отрезками прямых.

На диаграмме располагаются все обозначения и надписи.

1. Надписи, касающиеся диаграммы (название, разметка числовых значений на осях, наименование контролируемого изделия (события), имя составителя диаграммы).
2. Надписи, касающиеся данных (период сбора информации, объект исследования и место его проведения, общее число объектов контроля).

Советы по построению диаграммы Парето:

1. Следует использовать разные классификации и составить как можно больше диаграмм Парето. Суть проблемы можно уловить, наблюдая явление с разных точек зрения, поэтому важно опробовать различные пути классификации данных, пока не выявятся немногочисленные важные факторы, что и служит целью анализа Парето.
2. Нежелательно, чтобы группа «прочие» факторы (или «другие») составляла большой процент. Если такое происходит, значит, объекты наблюдения расклассифицированы неправильно и слишком много объектов попало в одну группу. В этом случае надо использовать другой принцип классификации.
3. Если данные можно представить в денежном выражении, лучше всего показать это на вертикальных осях диаграммы Парето. Если нельзя оценить существующую проблему в денежном выражении, само исследование может оказаться неэффективным. Затраты – важный критерий изменений в управлении.

Практический пример построения диаграммы Парето

Диаграмма Парето – это способ графического изображения данных, для того, чтобы выявить, какое количество причин, оказывающих наиболее сильное влияние на появление данного следствия, в действительности существует.

В построении диаграммы Парето выделяют четыре шага (этапа). Для облегчения понимания того, как следует работать над диаграммой, рассмотрим простой пример [9]. Он взят из практики работы небольшой типографии, которая пыталась установить, какие из стоящих перед ней проблем являются наиболее серьезными и требуют рассмотрения в первую очередь.

В результате предварительной работы группы были определены типы проблем, по причине которых типография терпела убытки, затем в течение определенного времени были собраны соответствующие данные. Все собранные данные расположили в таблице, в порядке убывания их значений (таблица 7).

Затем на основании данных таблицы построили столбиковую диаграмму, наглядно иллюстрирующую количество случаев, возникающих по различным причинам. Для этого по горизонтальной оси были отложены сами проблемы, по вертикальной оси – количество случаев, соответствующих каждой проблеме. Отдельно выделили множество незначительных проблем (неправильный выбор бумаги, проблемы с типографской краской, повреждения при перевозке и др.).

Таблица 7

№	Проблема	Количество случаев	Доля в общем количестве случаев, %
	Дефекты печати
	Нарушение сроков
	Ошибки при верстке
	Повреждения при упаковке
	Другие:	(15)
	- неправильный выбор бумаги
	- проблемы с типографской краской
	- повреждения при перевозке
	- повреждения на конвейере
	- наклейки
	- балансировка печатных станков
	Всего

 

Рис. 25. Столбиковая диаграмма количества случав различных проблем типографии.

Для построения диаграммы Парето (а строится она по накопленным значениям причин) добавим колонки в таблицу 7 – накопленную сумма значений (нарастающий итог количества случаев) и накопленный процент (таблица 8).

Таблица 8

№	Проблема	Количество случаев	Накопленная сумма	Накопленный процент
	Дефекты печати
	Нарушение сроков
	Ошибки при верстке
	Повреждения при упаковке
	Другие
	Всего

На данном шаге по данным таблицы 8 построили кумулятивную кривую – диаграмму Парето. Для этого начертили 3 основные оси для построения графика. Горизонтальная ось – для самих проблем, вертикальная ось слева предназначена для количества случаев каждого типа проблем, вертикальная ось справа – для обозначения процентов, показывающих долю в общей сумме накопленных значений. Данная ось послужит для обеспечения интерпретации диаграммы с помощью процентных соотношений. Верхний предел вертикальной оси слева определяется общей суммой собранных данных, в нашем примере это 85.

Провели пунктирную прямую от 80 % процентной оси на линию накопленных значений. Там, где эта прямая пересекает диаграмму, на горизонтальной оси определили, какая часть соответствует данному значению. В идеале она должна соответствовать 20 %.

Деления на горизонтальной оси наносятся с учетом общего числа категорий рассматриваемых проблем, при этом следует помнить, что проблемы под заголовком «Другие» объединены в одну категорию. В этом примере отличили 5 категорий проблем: четыре главные плюс еще одна под заголовком «Другие».

 

 

Рис. 26. Диаграмма Парето накопленных случаев различных проблем типографии

Как видно из законченной диаграммы, первые три проблемы (число которых соответствует 30 % первоначального списка из 10 категорий случаев) возникли примерно в 75 % случаях. Диаграмма Парето в данном формате высвечивает ключевые области и помогает группам установить приоритеты в своей деятельности.

На данном этапе важно подчеркнуть, что группы по решению проблем должны тщательно исследовать собранную информацию, а не считать наиболее вескими самые очевидные факты. О таких данных и пойдет речь далее. На первый взгляд, проблема «Дефекты печати» кажется ключевой и подлежит рассмотрению в первую очередь. Нас, конечно, интересует, какие проблемы наиболее часто встречаются, но еще больше нас волнует, какие затраты они привносят.

К счастью, группа не пошла по пути наименьшего сопротивления и решила на данном этапе продолжить исследование информации. Группа выяснила, какие затраты связаны с возникновением каждой проблемы, и построила на основе этих данных новую диаграмму Парето. Получив информацию по издержкам, группа расположила данные по-новому: по убыванию величины расходов, а не количества случаев. Результаты разительно отличались от полученных ранее, и это ясно показывает приведенная ниже таблица 9.

Проблемы с незначительными расходами были также объединены под заголовком «Другие» и добавлена графа «Нарастающий итог», в которой суммировались расходы, вызванные каждой проблемой. Таблица 9

№	Проблема	Количество случаев	Расходы руб.	Доля в общем количестве случаев, %	Нарастающий итог руб.	Доля, %
	Нарушение сроков		66 300		66 300
	Дефекты печати		21 400		87 700
	Повреждения при упаковке		10 500		98 200
	Ошибки при верстке		5 900		104 100
	Повреждения при перевозке		3 400		107 500
	Другие:		4 200		111 700
	Наклейки		1 900
	Неправильный выбор бумаги		1 080	0,9
	Проблемы с типографской краской			0,5
	Балансировка печатных станков			0,5
	Повреждения на конвейере			0,1
	Всего:		111 700

 

 

 

 

 

Рис. 27. Столбиковая диаграмма накопленных расходов при возникновении различных проблем типографии

 

Затем на основании новых данных построили кумулятивную кривую (диаграмму Парето).

 

 

Рис. 28. Диаграмма Парето расходов по различным проблемам типографии.

Вторая диаграмма Парето ясно показывает, какие проблемы являются приоритетными, если брать за основу расходы, связанные с ними.

В данном случае две категории расходов (20% от первоначального списка из 10 категорий) составляли приблизительно 80 % суммарных расходов по всем проблемам, причем около 60 % всех расходов приходится на категорию «Нарушение сроков».

Приведенный приме еще раз подтверждает необходимость тщательного исследования всех полученных данных. Диаграмма Парето – это простой и наглядный способ выполнения таких работ, который имеется в арсенале методов решения проблем.

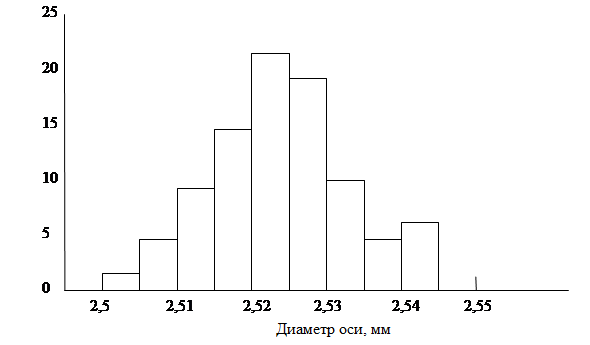
Построение диаграммы Парето состоит из следующих шагов:

1. Расположить данные в порядке убывания значений и просуммировать их.

2. Выделить часть данных, не имеющих приоритетного значения, под заголовком «Другие» и добавить графу «Нарастающий итог».

3. Подготовить оси для построения диаграммы и добавить справа дополнительную вертикальную ось для процентов.

4. Построить столбцы диаграммы и итоговую кривую.

Можно исследовать другие возможные варианты диаграммы Парето, построенные на тех же самых данных.

Гистограммы

Одним из наиболее распространенных методов, помогающих интерпретировать данные по исследуемой проблеме, является гистограмма. Гистограммы позволяют исследовать различные статистические данные, такие как, например, заработная плата в фирме различных категорий работников, изменение роста людей, количество пенсионеров разного возраста и другие. В производстве – это распределение измеряемого параметра, определение размеров классов, причины дефектов, отказов и т. д.

Большая часть всех совокупностей данных подчиняется так называемому «нормальному» распределению [15]. Если собрать все данные о процессе, в котором все факторы (человек, машина, материал, метод и т. д.) строго постоянны, то они оказались бы одинаковыми. Однако в действительности невозможно сохранять постоянство всех факторов. Несмотря на стремление удержать на постоянном уровне условия, подлежащие изменениям, в показателях все-таки наблюдается рассеивание значений. Даже те несколько факторов, которые считаются постоянными, на самом деле будут изменяться. Такого рода рассеивания можно разделить на две категории:

· неизбежное рассеивание значений,

· устранимое рассеивание значений.

Неизбежное рассеивание представляет собой случайные погрешности производства, которые возникают либо из-за колебаний в качестве сырья и материалов (в пределах допустимых отклонений), либо из-за изменений в условиях производства (также в пределах допустимых отклонений), устранять эту категорию рассеивания неэкономично.

Устранимое рассеивание представляет собой систематическую погрешность производства, которая возникает либо в результате использования нестандартного сырья и материалов, либо из-за нарушений технологического режима при выполнении операций, либо вследствие осуществления их по технологической документации, которая недоработана, либо в результате неожиданной разладки оборудования. Таким образом, это происходит по определенной причине и представляет собой устранимое явление, которое непременно следует устранять.

Построение диаграммы производится в несколько шагов. Рассмотрим построение гистограммы на конкретном примере [15].

Для исследования распределения диаметров стальных осей, изготовленных на токарном станке, были измерены диаметры 90 осей.

Необходимо по собранным данным вычислить величину выборочного размаха. Для этого следует выбрать наименьшее и наибольшее значения измеряемых величин. Исходные данные представлены в таблице 10.

Таблица 10

Номер выборки	Результаты измерений, см
1 – 10	2,510	2,517	2,522	2,510	2,511	2,519	2,532	2,543	2,525	2,522
11 – 20	2,527	2,536	2,506	2,541	2,512	2,515	2,521	2,536	2,529	2,524
21 – 30	2,529	2,523	2,523	2,523	2,519	2,528	2,543	2,538	2,518	2,534
31 – 40	2,520	2,514	2,512	2,534	2,526	2,530	2,532	2,526	2,523	2,520
41 – 50	2,535	2,523	2,526	2,525	2,532	2,522	2,501	2,530	2,522	2,514
51 – 60	2,533	2,510	2,542	2,524	2,530	2,521	2,522	2,535	2,540	2,528
61 – 70	2,525	2,515	2,520	2,519	2,526	2,527	2,522	2,542	2,540	2,528
71 – 80	2,531	2,545	2,524	2,522	2,520	2,519	2,519	2,529	2,522	2,513
81 – 90	2,518	2,527	2,511	2,519	2,531	2,527	2,529	2,528	2,519	2,521

 

Наибольшие и наименьшие значения можно получить следующим образом: сначала надо найти наибольшее и наименьшее значения в каждой строке таблицы исходных данных, а затем взять самое большое из максимумов и самое маленькое из минимумов. Это и будет максимум и минимум всех наблюдаемых значений (табл. 11): 2,545 и 2,502, соответственно. Выборочный размах равен разности между максимальным и минимальным значениями.

 

Таблица 11

Номер образца	Результаты измерения, см	Макс. в строке	Миним. в строке
1 – 10	2,510	2,517	2,522	2,510	2,511	2,519	2,532	2,543	2,525	2,522	2,543	2,510
11 – 20	2,527	2,536	2,506	2,541	2,512	2,515	2,521	2,536	2,529	2,524	2,541	2,506
21 – 30	2,529	2,523	2,523	2,523	2,519	2,528	2,543	2,538	2,518	2,534	2,543	2,518
31 – 40	2,520	2,514	2,512	2,534	2,526	2,530	2,532	2,526	2,523	2,520	2,534	2,512
41 – 50	2,535	2,523	2,526	2,525	2,532	2,522	2,501	2,530	2,522	2,514	2,535	2,502
51 – 60	2,533	2,510	2,542	2,524	2,530	2,521	2,522	2,535	2,540	2,528	2,542	2,510
61 – 70	2,525	2,515	2,520	2,519	2,526	2,527	2,522	2,542	2,540	2,528	2,542	2,515
71 – 80	2,531	2,545	2,524	2,522	2,520	2,519	2,519	2,529	2,522	2,513	2,545	2,513
81 - 90	2,518	2,527	2,511	2,519	2,531	2,527	2,529	2,528	2,519	2,521	2,531	2,511

Далее необходимо разделить выборочный размах на интервалы равной ширины: обычно делят от 5 до 20 интервалов. При числе наблюдений 11 и более используют более узкий интервал, при 99 наблюдениях и меньше – более широкий.

Теперь требуется по иному распределить данные, для этого готовят новую таблицу, куда заносят диапазон значений каждого интервала, среднюю точку, подсчет количества (частот) и саму частоту попаданий данных в соответствующий интервал.

Далее следует определить границы интервалов таким образом, чтобы они включали в себя наименьшее и наибольшее значения. Кроме того, важно, чтобы никакие значения наблюдений не попадали на границу интервала, для этого, если значения данных, например, имеют 2 знака после запятой, то нижняя граница будет иметь 3 знака после запятой (- 0,005) от соответствующего значения.

После этого следует убедиться в том, что первый интервал включает в себя наименьшее значение и что его граничное значение приходится на середину принятой единицы измерения (т. е. число 5 в следующем десятичном разряде). Далее, продолжая прибавлять выбранный интервал к предыдущему значению для получения второй границы, затем третьей и т. д., необходимо удостовериться, что последний интервал включает в себя максимальное значение.

Для получения частот надо подсчитать, какое количество значений из табл. попадает внутрь каждого из интервалов, и записать частоты, приходящиеся на каждый интервал, используя наклонные черточки, сгруппированные по пять, и записать в таблицу.

На данном шаге строится диаграмма. На листе в клеточку необходимо нанести горизонтальную ось, выбрать масштаб и нанести соответствующие интервалы (табл. 12). Далее строится вертикальная ось, на которой также выбирается масштаб в соответствии с максимальным значением частот.

 

Таблица 12

Номер класса	Класс	Середина класса, х	Подсчет частот	Частота, f
	2,5005 – 2,5055	2,503	/
	2,5055 – 2,5105	2,508	////
	2,5105 – 2,5155	2,513	//// ////
	2,5155 – 2,5205	2,518	//// //// ////
	2,5205 – 2,5255	2,523	//// //// //// //// //
	2,5255 – 2,5305	2,528	//// //// //// ////
	2,5305 – 2,5355	2,533	//// ////
	2,5355 – 2,5405	2,538	////
	2,5405 – 2,455	2,543	//// /
	Итого:

 

Количество измерений: n = 90

Наибольшее значение – 2,545

Наименьшее значение – 2,502

 

Рис. 29. Гистограмма распределения измерений

Шаг 5

Теперь необходимо проанализировать полученную гистограмму. Данная гистограмма (рис. 29) подчиняется нормальному распределению. То есть, предварительно можно сказать, что такой процесс встречается чаще всего.

Анализ гистограммы можно провести по трем направлениям.

1. Чтение гистограмм

Не все данные подчиняются закону нормального распределения [15]. Есть и другие типичные варианты распределения, по которым мы можем судить о ходе процесса.

 

 

Рис. 30. Варианты распределения данных

Несимметричное распределение. Такая форма встречается, когда верхняя (нижняя) граница регулируется либо теоретически, либо по значению допуска или когда левое (правое) значение недостижимо.

Бимодальное распределение. Такая форма встречается, когда смешиваются два распределения с далеко отстоящими средними значениями.

Равномерное распределение. Такая форма встречается в смеси нескольких распределений, имеющих различные средние.

Мультомодальное распределение. Такая форма встречается, когда число единичных наблюдений, попадающих в класс, колеблется от класса к классу или когда действует определенное правило округления данных.

Распределение с обрывом слева (или справа). Это одна из тех форм, которые часто встречаются при 100%-ном контроле изделий из-за плохой воспроизводимости процесса, а также когда проявляется резко выраженная положительная (отрицательная) симметрия.

Распределение с обрывом слева. Это форма, которая появляется при наличии малых включений данных из другого распределения, как, скажем, в случае нарушения нормальности процесса, появления погрешности измерения или просто включения данных из другого процесса.

1. Вариабельность процесса

Вариабельность (или изменчивость) присуща всем природным явлениям, всем техническим и технологическим процессам, а также всем организационным структурам. На выходе любого процесса мы всегда получаем не строго одно и то же значение, а набор значений, группирующихся вокруг некоторого значения (при условии, что с процессом все в порядке, это значение будет совпадать с номиналом). Эти отклонения называют вариациями, а общее название, описывающее эту ситуацию – вариабельность.

Гистограмма распределения данных всегда имеет верхнюю и нижнюю границы допуска. Если даже все столбики данных укладываются внутри этих границ, то можно судить о степени вариабельности. Чем число столбиков меньше и оно приближается к номинальному значению, тем лучше для процесса, значит он стабилен. Если столбики гистограммы присутствуют на всем интервале между верхней и нижней границами допуска – процесс необходимо улучшать.

Кому и когда необходимо вмешиваться в процесс?

Когда все столбики укладываются в пределах границ допуска – это значит, что имеют место общие причины вариаций. Они связаны с неабсолютной точностью поддержания параметров и условий осуществления процесса, а также условий на входе и выходе и т. д. Другими словами, это результат совместного воздействия большого числа случайных факторов, каждый из которых вносит небольшой вклад в результирующую вариацию и влияние которых почти невозможно отделить друг от друга. В этом случае для уменьшения вариабельности необходимо совершенствовать сам процесс, т. е. это могут осуществить только высшие руководители.

В случае, когда какие-то столбики выходят за границы верхнего и нижнего допуска следует искать специальные причины вариаций, которые возникают из-за внешних воздействий по отношению к процессу и которые не являются его неотъемлемой частью. Другими словами, это те причины, которые возникают в результате конкретных случайных воздействий на процесс, причем именно данная конкретная причина и приводит к данному конкретному отклонению параметров или характеристик процесса от заданных значений. В этом случае причину необходимо определить и устранить непосредственно на рабочем месте. Такие причины отклонений не требуют вмешательства в систему.

1. Анализ нормального распределения

Если предварительного анализа недостаточно, то можно дальше исследовать гистограмму математическими средствами. Характеристики нормального распределения могут сильно измениться, если наращивать число данных исследования. Определить это можно расчетным способом. По среднему арифметическому и стандартному отклонению полученной гистограммы можно рассчитать нормальное распределение для большого числа данных (а не для выборки, по которой гистограмма строится обычно) и представить его графически. А далее рассчитать индексы воспроизводимости и долю брака (или нарушений процесса).

Алгоритм данного исследования достаточно сложен, поэтому осуществлять данный вид анализа лучше специалисту, хорошо владеющему математическим аппаратом.

С учетом всех данных, группа должна ответить на следующий вопрос: «Почему данные имеют именно такое распределение, и что полезного мы можем извлечь из этого для решения рассматриваемой проблемы?»

Построение гистограммы включает в себя 6 шагов:

1. Записать данные, выявите максимальное и минимальное значения, распределите в порядке убывания.

1. Разделить диапазон значений на несколько равных частей и соотнесите имеющиеся данные с той или иной частью диапазона.
2. Определить границы интервалов.
3. Построить гистограмму.
4. Проанализировать гистограмму.
5. Задать вопрос: «Почему распределение именно такое, и о чем это нам говорит?»

 

Диаграммы Парето и гистограммы — два метода, которые очень часто применяют группы для интерпретации собранных данных. Иногда бывает достаточно построить простой линейный график, круговую диаграмму или использовать другие наглядные способы, чтобы значительно ускорить решение проблемы, так как визуальная форма подачи информации помогает лучше понять данные и ускоряет процесс решения проблемы.

 

Глава 9. ПОИСК РЕШЕНИЙ

Пути решения

После того как группа провела анализ проблем и собрала дополнительную информацию, уточняющую причины проблемы, необходимо определить пути ее решения. В этом случае необходимо применить самые разнообразные методы, побуждающие и к аналитическому, и к творческому мышлению, так как разные группы рассматривают разные проблемы, требующие соответственно различного подхода к их решению.

Группы, решающие проблемы, должны отдавать себе отчет в том, что они хотят решить. Многие возможные решения проблем не будут реалистичными, поскольку либо у сотрудников, либо у организации недостаточно ресурсов для реализации принятых решений. Кроме того, причиной проблемы могут быть находящиеся внутри организации силы, – например законы, которые руководство или специалисты не властны изменить.

Ограничения корректирующих действий сужают возможности в принятии решений. Перед тем как переходить к следующему этапу процесса, группы должны беспристрастно определить суть ограничений и только потом выявлять альтернативы. Если этого не сделать, то, как минимум, будет впустую потеряна масса времени. Еще хуже, если будет выбрано нереалистичное направление действий. Естественно, это усугубит, а не разрешит существующую проблему.

Ограничения варьируются и во многом зависят от ситуации и конкретных условий функционирования данной организации. Рассмотрим наиболее общие ограничения для различных организаций:

· неадекватность имеющихся средств,

· недостаточное число работников, имеющих требуемую квалификацию и опыт,

· неспособность закупить ресурсы по приемлемым ценам,

· потребность в технологии, еще не разработанной или чересчур дорогой,

· наличие острой конкуренции,

· законы и этические соображения.

Как правило, для крупной организации, обладающей достаточными средствами, существует меньше ограничений, чем для мелкой или организации, одолеваемой множеством трудностей.

В дополнение к идентификации ограничений группам необходимо определить стандарты, по которым предстоит оценивать альтернативные варианты выбора. Эти стандарты принято называть критериями принятия решения. Они выступают в качестве рекомендаций по оценке решений. Например, принимая решение о покупке автомобиля, вы можете ориентироваться на критерии стоимости, экономичности (расход бензина на определенное количество километров), вместимости, привлекательности и на хорошие сервисные характеристики.

После того необходимо сформулировать набор альтернативных решений проблемы. Это, собственно, и есть основная цель данного этапа. В идеале, группам желательно выявить все возможные действия, которые могли бы устранить причины проблемы и, тем самым, дать возможность организации достичь своих целей. Но нельзя забывать, что большое число альтернатив, даже если все они реалистичны, часто ведет к путанице. Поэтому участники группы должны ограничить число вариантов выбора для серьезного рассмотрения всего несколькими альтернативами, которые представляются наиболее значительными.

Часто вместо поиска наилучшего возможного решения, устраняющего корни проблемы, люди продолжают перебирать альтернативы до тех пор, пока не выявится такая, которая удовлетворяет определенному минимальному стандарту. Группы не могут себе позволить ограничиваться подобным вариантом – они призваны искать именно корни проблемы, поэтому критерий времени не играет решающей роли в поиске.

Группам следует позаботиться о том, чтобы был учтен достаточно широкий спектр возможных решений. Отобрав достаточное количество альтернатив, необходимо оценить их.

При выявлении возможных альтернатив необходима определенная предварительная оценка. Исследования в этой области показали, что как количество, так и качество альтернативных идей растет, когда начальная генерация идей отделена от оценки окончательной цели.

Это означает, что только после составления группами списка всех идей, следует переходить к оценке каждой альтернативы. При оценке решений участниками определяются достоинства и недостатки каждого из них и возможные общие последствия. Для сопоставления решений необходимо искать наиболее важные стандарты (или критерии), относительно которых можно измерить вероятные результаты реализации каждой возможной проблемы.

Описанные ниже методы позволяют учитывать самые разные возможности и являются полезным дополнением к набору уже имеющихся в арсенале отдельных исследователей и групп. Не все они взаимозаменяемы; некоторые из них разработаны для применения в специфических обстоятельствах, связанных с характером работы группы или рассматриваемой проблемы.

В данной главе рассматриваются методы (например, метод Дельфи и обмен мнениями), при помощи которых можно выбрать альтернативные варианты решений. Но сначала необходимо провести мозговой штурм по выдвижению этих идей. Сделать это можно при помощи уже рассмотренных ранее методов:

· метод «бритва Оккама»,

· диаграмма сродства,

· древовидная диаграмма,

· а также методы, предложенные для рассмотрения в данной главе – анализ силового поля, коллажи и фантазии и матричная диаграмма.

Также при решении производственных задач целесообразно использовать методику построения диаграммы «рыбьи кости». Только в данном случае в левой части листа располагают формулировку желаемого результата, от нее проводится линия (хребет рыбы), затем определяются главные заголовки областей, которые будут неизбежно затронуты при реализации данного решения, далее – детализировать по уровням 2-го, 3-го и т. д. порядка.

Рассмотрим методы более подробно.

Анализ силового поля

Анализ силового поля был разработан Куртом Левиным для того, чтобы проблемы могли быть представлены наглядно [9]. Этот метод опирается главным образом на аналитическое мышление. Он применяется при рассмотрении множества ситуаций и должен находиться в арсенале всех групп, решающих проблемы.

Данный метод представляет каждую проблему как баланс двух противоположно направленных систем сил. Силы одной из этих систем пытаются изменить текущую ситуацию в лучшую сторону и называются движущими. Противостоящие им силы стремятся изменить ситуацию в худшую сторону и называются сдерживающими. На диаграмме это выглядит следующим образом (рис. 31):

 

 

 

Рис. 31. Диаграмма сил и факторов, содействующих и препятствующих решению проблемы

Анализ силового поля состоит из шести шагов.

Группа должна определить наихудшую и идеальную из возможных ситуаций, касающихся данной проблемы. После анализа решаемой проблемы, сбора и интерпретации данных текущее состояние дел должно стать более понятным. Для этого следует записать на отдельных больших листах наилучший и наихудший сценарии развития ситуации и поместить их на левом и правом краях поля из трех больших листов, разлинованного как показано ниже в таблице 13:

Таблица 13

СИТУАЦИЯ
Наихудшая	текущая	Идеальная
Важность силы	Легкость изменения силы	Важность силы	Легкость изменения силы
группой	другими людьми	группой	другими людьми
Движущие силы							Сдерживающие силы
Лист 1	Лист 2	Лист 3

Далее группа обсуждает и согласовывает сдержив