
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенциал поля точечного заряда (1.6)Содержание книги Поиск на нашем сайте
Электростатика 1.1 Закон сохранения заряда. Закон Кулона. Напряженность электрического поля. Напряженность поля точечного заряда. Принцип суперпозиции.
А. закон сохранения заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы ни происходили внутри этой системы Б. Закон Кулона: сила взаимодействия между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам и обратно пропорциональна квадрату расстояния между нимиF=
В. Напряженность электростатического поля – 1)отношение силы действующей на заряд к величине этого заряда. E= 2) Если g=1 то Е=F, напряженность- сила действующая на единичный положительный заряд Г.Е=К Д. Напряженность результирующего поля есть алгебраическая сумма всех полей Е=
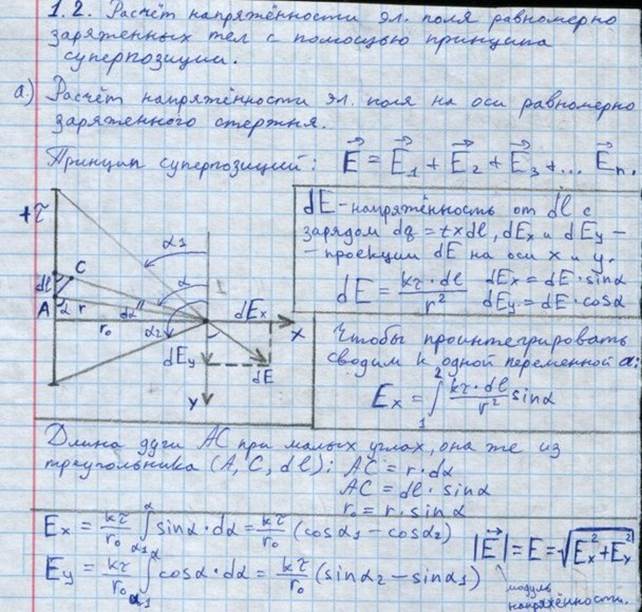
1.2 Расчет напряженности электрического поля равномерно заряженных тел с помощью принципа суперпозиции: а) расчет напряженности электрического поля на оси равномерно заряженного стержня;
б) расчет напряженности электрического поля на оси равномерно заряженного тонкого кольца;
1.3 Поток вектора напряженности электрического поля. Теорема Гаусса.
1.4 Расчет напряженности электрического поля равномерно заряженных тел с помощью теоремы Гаусса: а) плоскости; б) нити; в) шара. а) плоскости; 1. Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис. 126) заряжена с постоянной поверхностной плотностью +s(s = d Q/ d S — заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (соsa=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равенсумме потоков сквозь его основания (площади оснований равны и для основания Еn совпадает с Е), т. е. равен 2 ES. Заряд, заключенный внутри построенной цилиндрической поверхности, равен s S. Согласно теореме Гаусса (81.2), 2 ES= s S/ e0, откуда
Из формулы (82.1) вытекает, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно. 2. Поле двух бесконечных параллельных разноименно заряженных плоскостей (рис. 127). Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями + sи –s. Поле таких плоскостей найдемкак суперпозицию полей, создаваемых каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние — от отрицательной плоскости. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля E =0. В области между плоскостями E = E + + E – (E + и E – определяются по формуле (82.1)), поэтому результирующая напряженность
Таким образом, результирующая напряженность поля в области между плоскостями описывается формулой (82.2), а вне объема, ограниченного плоскостями, равна нулю.
б) нити; 5. Поле равномерно заряженного бесконечного цилиндра (нити). Бесконечный цилиндр радиуса R (рис. 131) заряжен равномерно с линейной плотностью t (t =
Если r<R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области E=0. Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра определяется выражением (82.5), внутри же его поле отсутствует. в) шара. 3. Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью +s. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально (рис. 128). Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r>R,ro внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса (81.2),
При r>R поле убывает с расстоянием r по такому же закону,как у точечного заряда. График зависимости Е от r приведен на рис. 129. Если r'<R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (E =0). 4. Поле объемно заряженного шара. Шар радиуса R с общим зарядом Q заряжен равномерно собъемной плотностью r(r = симметрии (см. п. 3), можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае (см. (82.3)). Внутри же шара напряженность поля будет другая. Сфера радиуса r'<R охватывает заряд Q'= 4/3
Таким образом, напряженность поля вне равномерно заряженного шара описывается формулой (82.3), а внутри его изменяется линейно с расстоянием r' согласно выражению (82.4). График зависимости Е от r для рассмотренного случая приведен на рис. 130.
е отсутствует (E =0).
1.5 Работа перемещения заряда в электрическом поле. Циркуляция вектора напряженности электростатического поля.
Работа перемещения заряда. На положительный точечный заряд q в электрическом поле с напряжённостью E действует сила d A = F d l =q E d l cos (E, d l ). При перемещении заряда q силами электрического поля на произвольном конечном отрезке из точки 1 в точку 2 эта работа равна Рассмотрим перемещение точечного заряда q в поле точечного заряда Q, напряженность поля которого Проекция отрезка d l на направление вектора E (рис. 1.5) есть d r = d l cos (E, d l). Работа, совершаемая электрическим полем при перемещении заряда q из точки 1 в точку 2, определяется следующим образом:
Отсюда следует, что работа сил электрического поля не зависит от формы пути, а определяется только начальным и конечным положениями заряда q. Если оба заряда, q и Q, положительны, то работа сил поля положительна при удалении зарядов и отрицательна при их взаимном сближении. Для электрического поля, созданного системой зарядов Q 1, Q 2,¼, Qn, работа перемещения заряда q равна алгебраической сумме работ составляющих сил: Таким же образом, как и каждая из составляющих работ, суммарная работа зависит только от начального и конечного положений заряда q. Циркуляция вектора напряженности электрического поля. Работа, совершаемая силами электрического поля при перемещении единичногоположительного заряда по замкнутому контуру длиной l, определяется как циркуляция вектора напряженности электрического поля: Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т.е. Равенство нулю означает, что силы электрического поля являются силами консервативными, а само поле - потенциальным.
1.6 Потенциал. Потенциал поля точечного заряда. Принцип суперпозиции для потенциала поля системы зарядов Электростатический потенциал — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда.
Электрический ток 2.1. Электрический ток; сила и плотность тока. Электрическим током называется направленное (упорядоченное) движение заряженных частиц. СИЛА ТОКА – скалярная физическая велична, равная количеству электрического заряда, переносимосму за единицу времени через поперечное сечение проводника S.
Ток, сила и направление которого не изменяются со временем, называется постоянным. ПЛОТНОСТЬ ТОКА
2.2 Условия существования электрического тока. Сторонние силы, ЭДС, падение напряжения.
2.3 Закон Ома в интегральной и дифференциальной формах. Сопротивление проводников и его зависимость от температуры. Соединения проводников. 2.4 Работа и мощность электрического тока. Закон Джоуля - Ленца в интегральной и дифференциальной формах.
РАБОТА ЭЛЕКТРИЧЕСКОГО ТОКА Работа электрического тока показывает, какая работа была совершена электрическим полем при перемещении зарядов по проводнику. Зная две формулы:
Работа электрического тока равна произведению силы тока на напряжение Единица измерения работы электрического тока в системе СИ: Электромагнетизм 3.1. Магнитное поле (м.п.) в вакууме. Сила Ампера. Магнитная индукция (В). Принцип суперпозиции для В. Закон Био - Савара – Лапласа (Б-С-Л). 3.2. Применение закона Б-С-Л для расчета: a. Индукции магнитного поля прямого тока
Магнитное поле в центре кругового проводника с током(рис. 166). Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитное поле одинакового направления — вдоль нормали от витка.
Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sina=1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то,
Тогда
Следовательно, магнитная индукция поля в центре кругового проводника с током
b. Индукции магнитного поля в центре кругового витка
c. Индукции магнитного поля на оси кругового витка
d. Индукции магнитного поля проводника конечных размеров
3.3. Закон Ампера.
Закон Ампера устанавливает, что на проводник с током, помещенный в однородное магнитное поле, индукция которого В, действует сила, пропорциональная силе тока и индукции магнитного поля: F = BI l sina (a - угол между направлением тока и индукцией магнитного поля). Закон Ампера принимает вид: dF = I*B*dlsina Закон Ампера в векторной форме: dF = I [dl B] Сила Ампера направлена перпендикулярно плоскости, в которой лежат векторы dl и B.
3.4. Линии индукции магнитного поля (вектора В). Магнитный поток. Теорема Гаусса для В. 3.5. Теорема о циркуляции вектора В.
Правило Ленца Ток, индуцируемый при изменении магнитного поля проходящего через контур, своим магнитным полем препятствует этому изменению.
3.15. Расчет ЭДС индукции:
a. при движении проводника в магнитном поле.
b. в замкнутом контуре, при изменении магнитного поля.
3.16. Явление самоиндукции. Индуктивность. Индуктивность соленоида.
3.17. Энергия магнитного поля. Объемная плотность энергии магнитного поля.
1.Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре.
2.Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I: Φ = LI. 2 вопрос Объемная плотность энергии магнитного поля вычисляется по формуле: w м= B 22 μμ 0, где B − магнитная индукция, μ − магнитная проницаемость, μ 0=4 π ⋅10−7 Гн/м − магнитная постоянная.
3.18. Явление взаимной индукции. Коэффициент взаимной индукции. Трансформаторы.
3.19. Магнитное поле в веществе. Намагниченность (вектор I). Токи намагничивания. Теорема о циркуляции I. Магнитноеполе в веществе складывается из двухполей: внешнего поля, создаваемоготоком, и поля, создаваемого намагни-ченным веществом. Тогда можем записать, что вектор магнитной индукциирезультирующего магнитного поля вмагнетике равен векторной сумме магнитных индукций внешнего поля В (создаваемого намагничивающим током в вакууме) и поля микротоков В' (создаваемого молекулярными токами):
Намагниченность:
Токи намагничивания I'. Намагничивание вещества связано с преимущественной ориентацией магнитных моментов отдельных молекул в одном направлении. Элементарные круговые токи, связанные с каждой молекулой, называются молекулярными. Молекулярные токи оказываются ориентированными, т.е. возникают токи намагничивания -
Циркуляция вектора намагниченности Дифференциальная форма записи теоремы о циркуляции вектора
Дифференциальная форма записи теоремы о циркуляции - формула (54.7) – ротор вектора
3.20. Вектор напряженности магнитного поля (вектор Н). Теорема о циркуляции вектора Н.
3.21. Связь между I и Н, В и Н. Магнитная восприимчивость, магнитная проницаемость. Классификация магнетиков.
3.22. Намагничивание диамагнетиков. Как мы уже говорили, магнетики можно разделить на три основные группы: диамагнетики, парамагнетики и ферромагнетики. Диамагнетизм (от греч. dia – расхождение и магнетизм) - свойство веществ намагничиваться навстречу приложенному магнитному полю. Диамагнетиками называются вещества, магнитные моменты атомов которых в отсутствии внешнего поля равны нулю, т.к. магнитные моменты всех электронов атома взаимно скомпенсированы (например инертные газы, водород, азот, NaCl и др.). При внесении диамагнитного вещества в магнитное поле его атомы приобретают наведенные магнитные моменты. В пределах малого объема Δ V изотропного диамагнетика наведенные магнитные моменты Вектор намагниченности диамагнетика равен:
где n 0 – концентрация атомов, Для всех диамагнетиков У диамагнетиков
3.23. Намагничивание парамагнетиков. Закон Кюри.
Закон Кюри — физический закон, описывает магнитную восприимчивость парамагнетиков, которая при постоянной температуре для этого вида материалов приблизительно прямо пропорциональна приложенному магнитному полю. Закон Кюри постулирует, что при изменении температуры и постоянном внешнем поле, степень намагниченности парамагнетиков обратно пропорциональна температуре:
где: Простые модели парамагнетиков основываются на предположении, что эти материалы состоят из частей или областей (парамагнетонов), которые не взаимодействуют друг с другом. Каждая область имеет собственный магнитный момент, который можно обозначить векторной величиной Энергия моментамагнитного поля может быть записана следующим образом:
Для того, чтобы упростить вывод, предположим, что каждая из областей рассматриваемого парамагнетикаимеет два состояния момента, направление которого может совпадать с направлением магнитного поля или быть направленным в противоположную сторону. В данном случае возможны только два значения магнитного момента
Магнитная восприимчивость парамагнетика как функция температуры.
3.24. Ферромагнетизм. Свойства ферромагнетиков. Гистерезис. Природа ферромагнетизма.
3.25. Положения теории Максвелла для электромагнитного поля. Вихревое электрическое поле.
Основные положения теории Максвелла: 1) Переменное магнитное поле порождает в окружающем пространстве вихревое электрическое поле. 2) Переменное электрическое поле порождает в окружающем пространстве магнитное поле. Вихревое магнитное поле
3.26. Ток смещения. Полный ток. 3.27. Система уравнений Максвелла в интегральной и дифференциальной формах.
Содержание этих уравнений заключается в следующем: 1. Циркуляция вектора 2. Поток вектора 3. Циркуляция вектора 4. Поток вектора
В то же время в случае стационарных полей (
4. Электромагнитные колебания и волны. 4.1. Электромагнитные колебания. Колебательный контур. Аналогия механических и электромагнитных колебаний.
4.2. Гармонические электромагнитные колебания. Колебательный контур. Дифференциальное уравнение, его решение, график. 4.3. Затухающие электромагнитные колебания. Колебательный контур. Дифференциальное уравнение, его решение, график. 4.4. Характеристики затухающих электромагнитных колебаний. Коэффициент затухания, логарифмический декремент, добротность.
1) время релаксации t -время, в течении которого амплитуда колебаний уменьшается в е раз. 2) логарифмический декремент затухания, представляющий логарифм отношения двух соседних амплитуд, т.е.
где N - число колебаний, совершаемых за время уменьшения амплитуды в e раз. 3) добротность колебательной системы
где E - энергия системы в момент времени t; 4) коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз.;
4.5. Вынужденные электромагнитные колебания. Дифференциальное уравнение, его решение.
Уравнение: Решение: q=qmcos(ωt+ψ)
4.6. Вынужденные электромагнитные колебания. Законы изменения напряжения на R, L, C. Векторная диаграмма. 4.7. Переменный электрический ток. Закон Ома, импеданс. Явление резонанса. Резонанс напряжений. Резонансные кривые. Добротность. 4.8. Электромагнитные волны.
Переменные электрические и магнитные поля не могут существовать независимо друг от друга. Нельзя создать переменное магнитное поле без того, чтобы одновременно не возникло и переменное электрическое поле, и наоборот. Электромагнитное поле представляет собой взаимосвязанные колебания электрического (Е) и магнитного (В) полей. Распространение единого электромагнитного поля в пространстве осуществляется посредством электромагнитных волн. Электростатика 1.1 Закон сохранения заряда. Закон Кулона. Напряженность электрического поля. Напряженность поля точечного заряда. Принцип суперпозиции.
А. закон сохранения заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы ни происходили внутри этой системы Б. Закон Кулона: сила взаимодействия между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам и обратно пропорциональна квадрату расстояния между нимиF=
В. Напряженность электростатического поля – 1)отношение силы действующей на заряд к величине этого заряда. E= 2) Если g=1 то Е=F, напряженность- сила действующая на единичный положительный заряд Г.Е=К Д. Напряженность результирующего поля есть алгебраическая сумма всех полей Е=
1.2 Расчет напряженности электрического поля равномерно заряженных тел с помощью принципа суперпозиции: а) расчет напряженности электрического поля на оси равномерно заряженного стержня;
б) расчет напряженности электрического поля на оси равномерно заряженного тонкого кольца;
1.3 Поток вектора напряженности электрического поля. Теорема Гаусса.
1.4 Расчет напряженности электрического поля равномерно заряженных тел с помощью теоремы Гаусса: а) плоскости; б) нити; в) шара. а) плоскости; 1. Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис. 126) заряжена с постоянной поверхностной плотностью +s(s = d Q/ d S — заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (соsa=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равенсумме потоков сквозь его основания (площади оснований равны и для основания Еn совпадает с Е), т. е. равен 2 ES. Заряд, заключенный внутри построенной цилиндрической поверхности, равен s S. Согласно теореме Гаусса (81.2), 2 ES= s S/ e0, откуда
Из формулы (82.1) вытекает, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно. 2. Поле двух бесконечных параллельных разноименно заряженных плоскостей (рис. 127). Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями + sи –s. Поле таких плоскостей найдемкак суперпозицию полей, создаваемых каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние — от отрицательной плоскости. Слева и справа от плоскостей поля вычитаются (линии напряженности направлены навстречу друг другу), поэтому здесь напряженность поля E =0. В области между плоскостями E = E + + E – (E + и E – определяются по формуле (82.1)), поэтому результирующая напряженность
Таким образом, результирующая напряженность поля в области между плоскостями описывается формулой (82.2), а вне объема, ограниченного плоскостями, равна нулю.
б) нити; 5. Поле равномерно заряженного бесконечного цилиндра (нити). Бесконечный цилиндр радиуса R (рис. 131) заряжен равномерно с линейной плотностью t (t =
Если r<R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области E=0. Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра определяется выражением (82.5), внутри же его поле отсутствует. в) шара. 3. Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью +s. Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально (рис. 128). Построим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r>R,ro внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса (81.2),
При r>R поле убывает с расстоянием r по такому же закону,как у точечного заряда. График зависимости Е от r приведен на рис. 129. Если r'<R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (E =0). 4. Поле объемно заряженного шара. Шар радиуса R с общим зарядом Q заряжен равномерно собъемной плотностью r(r = симметрии (см. п. 3), можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае (см. (82.3)). Внутри же шара напряженность поля будет другая. Сфера радиуса r'<R охватывает заряд Q'= 4/3
Таким образом, напряженность поля вне равномерно заряженного шара описывается формулой (82.3), а внутри его изменяется линейно с расстоянием r' согласно выражению (82.4). График зависимости Е от r для рассмотренного случая приведен на рис. 130.
е отсутствует (E =0).
1.5 Работа перемещения заряда в электрическом поле. Циркуляция вектора напряженности электростатического поля.
Работа перемещения заряда. На положительный точечный заряд q в электрическом поле с напряжённостью E действует сила
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 338; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.103.70 (0.015 с.) |









 (82.1)
(82.1) (82.2)
(82.2)
 – заряд, приходящийся на единицу длины). Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиуса r и высотой l. Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность равен 2p rlЕ. По теореме Гаусса (81.2), при r>R 2prlЕ = tl/e0, откуда
– заряд, приходящийся на единицу длины). Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиуса r и высотой l. Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность равен 2p rlЕ. По теореме Гаусса (81.2), при r>R 2prlЕ = tl/e0, откуда (82.5)
(82.5) , откуда
, откуда (82.3)
(82.3) . Поэтому, согласно теореме Гаусса (81.2),
. Поэтому, согласно теореме Гаусса (81.2),  . Учитывая, что
. Учитывая, что  , получаем
, получаем (82.4)
(82.4)
 .
. .
.

 .
.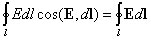
 .
. (Дж/Кл=В)
(Дж/Кл=В) - для постоянного тока, и
- для постоянного тока, и 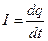 - для переменного тока.
- для переменного тока. - векторная физическая величина, численно равная силе тока, проходящего через единицу площади, перпендикулярной к току.
- векторная физическая величина, численно равная силе тока, проходящего через единицу площади, перпендикулярной к току. - для постоянного тока, и
- для постоянного тока, и  - для переменного тока.
- для переменного тока.


















 где
где 


 .
. по произвольному замкнутому контуру равна алгебраической сумме токов намагничивания, охватываемых контуром Г.
по произвольному замкнутому контуру равна алгебраической сумме токов намагничивания, охватываемых контуром Г.




 всех атомов одинаковы и направлены противоположно вектору
всех атомов одинаковы и направлены противоположно вектору  .
. ,
,
 – магнитная постоянная,
– магнитная постоянная,  –магнитная восприимчивость среды.
–магнитная восприимчивость среды. Таким образом, вектор
Таким образом, вектор  магнитной индукции собственного магнитного поля, создаваемого диамагнетиком при его намагничивании во внешнем поле
магнитной индукции собственного магнитного поля, создаваемого диамагнетиком при его намагничивании во внешнем поле  направлен в сторону, противоположную
направлен в сторону, противоположную 

 — получаемая намагниченность материала;
— получаемая намагниченность материала; 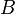 — магнитное поле, измеренное в теслах;
— магнитное поле, измеренное в теслах;  — абсолютная температура в кельвинах;
— абсолютная температура в кельвинах;  — постоянная кюри данного материала.
— постоянная кюри данного материала. .
.
 ,
,  и два значения энергии:
и два значения энергии:  и
и  .
.
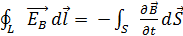 ,
, 




 по любому замкнутому контуру равна со знаком минус производной по времени от магнитного потока через любую поверхность, ограниченную данным контуром. При этом под
по любому замкнутому контуру равна со знаком минус производной по времени от магнитного потока через любую поверхность, ограниченную данным контуром. При этом под  сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью. (Фактически это теорема Гаусса для поля заряда, распределенного внутри замкнутой поверхности с объемной плотностью
сквозь любую замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью. (Фактически это теорема Гаусса для поля заряда, распределенного внутри замкнутой поверхности с объемной плотностью  )
) по любому замкнутому контуру равна полному току (току проводимости и току смещения) через произвольную поверхность, ограниченную данным контуром.
по любому замкнутому контуру равна полному току (току проводимости и току смещения) через произвольную поверхность, ограниченную данным контуром.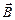 сквозь произвольную замкнутую поверхность всегда равна нулю. Данное уравнение постулирует отсутствие в природе «магнитных» зарядов. (Это теорема Гаусса для магнитного поля)
сквозь произвольную замкнутую поверхность всегда равна нулю. Данное уравнение постулирует отсутствие в природе «магнитных» зарядов. (Это теорема Гаусса для магнитного поля) и
и  ) система уравнений Максвелла распадается на две группы независимых уравнений:
) система уравнений Максвелла распадается на две группы независимых уравнений: ;
;  ;
; ;
;  .
.
 , (4.42)
, (4.42)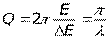 , (4.43)
, (4.43) -убыль энергии за один период колебаний.
-убыль энергии за один период колебаний.




