
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Величина под касательной вс равна сумме постоянных времениСодержание книги
Поиск на нашем сайте
Величину Т2 можно определить из выражения:
Это выражение трансцендентно, поэтому прямо определить Т2 нельзя. Оно может быть найдено как абсцисса точки пересечения двух функций:
В более сложных случаях, когда объект описывается уравнением выше второго порядка, используют один из перечисленных выше методов определения передаточных функций по кривой разгона. Достаточно прост и позволяет получить удобные для последующих расчетов выражения, метод последовательного логарифмирования [21].
3.2.4. Определение передаточной функции методом последовательного логарифмирования
В общем случае исследуемый объект описывается линейным дифференциальным уравнением с постоянными коэффициентами:
Если корни характеристического уравнения имеют действительные отрицательные значения, то его решение
Для определения коэффициентов Нк и Тк применим метод последовательного логарифмирования, который заключается в последовательном приближении функции h(t) решением уравнения первого порядка, т.е. функции
Если такая аппроксимация не удовлетворяет на каком-то отрезке времени, то рассматривается вторая составляющая
Итак, полагаем, что
Прологарифмируем это выражение
Вычисляем
Проводим асимптоту к полученной кривой (рис.15). На оси ординат она отсекает отрезок, равный lgH1 - при t = 0. Отсюда определим H1. Величина 1/T1 равна тангенсу наклона асимптоты к оси абсцисс
где t1 – точка пересечения с осью времени.
Рис.15 Если проведенная асимптота не совпадает со всеми значениями lg|h1(t)|, повышаем порядок дифференциального уравнения
Логарифмируем h2(t) и строим график lg|h2(t)|. Аналогично определяем Н2 и T2. Процесс прекращается, когда hn(t) = 0. При правильно определенных параметрах должны выполняться условия:
Продифференцируем уравнение переходной функции.
Преобразуем функцию по Лапласу
Отсюда,
Если объект обладает запаздыванием, то коэффициенты Нк, Тк определяются по переходной функции, из которой выделено чистое запаздывание.
При расчете удобно пользоваться таблицей по форме:
3.2.5. Определение передаточной функции объекта методом площадей
Одним из наиболее удобных методов расчета передаточных функций по кривой разгона с использованием ЭВМ является метод "площадей". Рассмотрим функцию h(t), которая получена из экспериментальной Обычно выражение для передаточной функции ищут в виде одной из трех математических моделей:
Выражение
Очевидно, что для модели (47) a1 = S1, a2 = S2, а3 = S3; для модели (48) a1 = S1, a2 = S2; для модели (49) коэффициенты bi, ai, i = 1,2,3... связаны с коэффициентами Si системой уравнений
Коэффициенты Si связаны с переходной функцией h(t) соотношениями:
Моментом i - го порядка функции (1 - h(t)) называется несобственный интеграл
Тогда формулы для S можно переписать:
Таким образом, определив по графику h(t) значение моментов Mi методом численного интегрирования и вычислив величины Si, можно найти значения коэффициентов передаточной функции. Выбор вида передаточной функции производится из следующих соображений: если коэффициенты S1, S2, S3 положительны, то задаются моделью (47) или (48). Если хотя бы один из них отрицателен - моделью (49). Ниже приведен пример программы расчета значений коэффициентов Si, i = 1...4, составленной на алгоритмическом языке Бейсик [9]. В программе N - число координат передаточной функции; X -шаг Δt во времени; P(I) - значение ординат функции h(t). Вычисление моментов Mi, i = 0....3 производятся по дискретным значениям переходной функции по формулам трапеций.
010 READ N,X 020 DIM P[30] 030 DIM Z[30] 040 LET M0 = M1 = M2 = M3 = M4 = 0 050 FOR I = I TO N 060 READ P[I] 070 LET Z [I] = (1 - P[I]) ∙ X 080 LET M1 = M0 + Z[I] 090 LET T = (I-1)∙X 100 LET M1 =M1 + Z[I]∙T 110 LET M2 = M2 + Z[I] ∙ Т – 2 120 LETM3 = M3 + Z[I]∙T-3 130 NEXT I 140 LET S1 = M0-Z[I]/2 150 LET S2 = S1 - 2 - M1 160 LET S3 = S2 ∙ M0 - S1 ∙ M1 + M2 / 2 170 LET S4 = S3∙M0 - S2∙M1 + S1∙M2/2 - M3/6 180 PRINT " S1 = ", S1," S2 = ", S2 185 GOTO 190 190 PRINT " S3 = ", S3," S4 = ",S4 200 DATA 23,1 210 DATA 0,2.00000E - 02,.12,.24,.35,.45,.55,.62,.69,.76,.79 220 DATA.83,.87,.89,.92,.94,.95,.96,.97,.98,.99,.99, 1 230 END
READY Перед обращением к программе из экспериментальной кривой В заключение проверяется точность аппроксимации. Обычно принимают, что модель адекватна объекту, если разность между ординатами нормированных передаточных функций модели и объекта не превышает 0.05…0.07.
4. Выбор регулятора
4.1. Выбор типа регулирования
Тип регулирования выбирается с учетом свойств объекта и заданных параметров переходного процесса. К параметрам переходного процесса могут предъявляться различные требования. В одних случаях оптимальным является процесс с минимальным значением динамической ошибки, в других - с минимальным значением времени регулирования и т.д. Обычно выбирают один из трех типовых переходных процессов: граничный апериодический, с 20% перерегулированием, с минимальной квадратичной площадью отклонения. Граничный апериодический процесс характеризуется отсутствием перерегулирования, минимальным общим временем регулирования и наименьшим воздействием регулятора на объект (что вызывает наибольшее отклонение регулируемой величины от заданного значения). Такой переходный процесс используется в качестве оптимального при значительном влиянии регулирующего воздействия на другие технологические величины объекта, чтобы свести их отклонение к минимуму. Процесс с 20% перерегулированием характерен большей величиной воздействия регулятора и меньшим отклонением, при этом время регулирования несколько возрастает. Этот процесс выбирают в качестве оптимального, когда допустимо небольшое перерегулирование. Процесс с минимальной квадратичной площадью отклонения обладает значительным перерегулированием (до 40%), большим временем регулирования и наименьшей величиной динамической ошибки. Ориентировочно характер действия регулятора определяется по отношению запаздывания τ к постоянной времени объекта Т. При При При Более подробно вопрос выбора типа регулятора рассмотрен в [21], где приведены необходимые алгоритмы и таблицы.
4.2. Выбор закона регулирования
В зависимости от типа уравнения связывающего величину отклонения регулирующей величины ε(t) и перемещение регулирующего органа Y(t) различают следующие законы регулирования.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 149; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.101.7 (0.006 с.) |

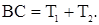



 .
.

 .
.
 .
.
 ,
,
 .
.
 .
.
 . Логарифмируем и строим график в десятичных логарифмах функции In | hi(t) | в зависимости от t
. Логарифмируем и строим график в десятичных логарифмах функции In | hi(t) | в зависимости от t .
.
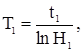


 ,
,
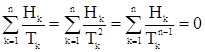 .
.
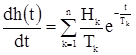 .
.
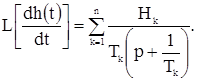

 .
.



 , обратное передаточной функции модели, можно разложить в ряд по степени р
, обратное передаточной функции модели, можно разложить в ряд по степени р

 ,
,
 ,
,
 ,
,
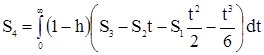 .
.
 .
.
 ,
,
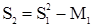 ,
,
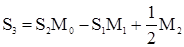 ,
,
 .
.
 выбирается позиционное регулирование.
выбирается позиционное регулирование. выбирается непрерывное регулирование, либо импульсное.
выбирается непрерывное регулирование, либо импульсное. применяют многоконтурные системы регулирования и принимают меры по компенсации влияния запаздывания.
применяют многоконтурные системы регулирования и принимают меры по компенсации влияния запаздывания.


