
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Подставляя относительные величиныСодержание книги Поиск на нашем сайте
Подставляя относительные величины
Получим:
Разделив все на F0Q0, получим:
где
Используя прямое преобразование Лапласа, запишем уравнение в операторной форме:
Передаточные функции по каналам:
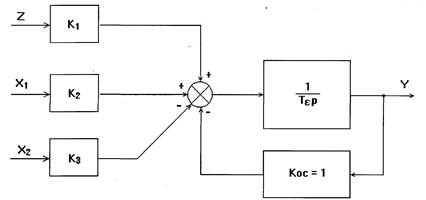
Уравнению (3) соответствует структурная схема:
Рис.7
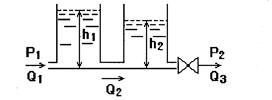
Пример 2. [18] Составить дифференциальное уравнение системы, образованной двумя баками (рис.8), приняв в качестве входной величины изменение расхода жидкости на притоке Q1, а выходной - изменение уровня h2 во втором по ходу жидкости баке.
Рис.8
Площади поперечного сечения баков S1 и S2. Допустим, что при малых отклонениях от исходного состояния равновесия расход Q2 между баками пропорционален разности уровней h1 и h2, а расход О3 не зависит от уровня h2. Из условия материального баланса для баков получим:
Учитывая, что
Продифференцируем по времени второе уравнение, учитывая, что Q3 = const
Определив из (13)
и подставив в (14), получим:
или
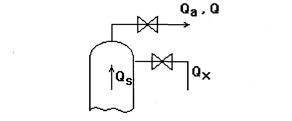
Пример З. Теплообменник смешения (рис. 9).
Рис.9
В теплообменнике регулируется температура паров продукта изменением количества холодной жидкости, подаваемой в теплообменник. Обозначим: Qs – количество тепла, поступающего в теплообменник с парами, ккал/мин; Qx – количество тепла, поступающего в теплообменник с холодной жидкостью, ккал/мин; Qa – количество тепла, уходящего из теплообменника с парами, ккал/мин; Θ – температура паров на выходе из теплообменника в °С; Gп – весовое количество паров, проходящих через теплообменник в кг/мин; G – весовое количество паров, содержащихся в теплообменнике в кг. В стационарном состоянии приток и расход тепла равны и температура остается постоянной. В случае изменения какого - либо количества тепла или одновременно всех количеств температура будет изменяться
где А - тепловая емкость объекта в ккал /°С. Положим, количество паров Gп, поступающих в теплообменник, и их температура остаются постоянными, т.е. Qs = 0, изменяется лишь количество тепла Qx, поступающего в теплообменник с холодной жидкостью. Тогда
Количество тепла, уходящего из теплообменника с парами, пропорционально количеству и их температуре, т.е.
где С – удельная теплоемкость в ккал/кг∙°С, ΔΘ – отклонение температуры. Тогда
Умножим и разделим члены левой части уравнения на заданное значение температуры Θн, и все уравнение разделим на номинальное значение теплоты qхн.
или
где
Пример 4. Резервуар для газа. В аппарат V м подается газ под давлением Рн (Па) (рис.10). Из аппарата газ выходит в количестве Fp (кг/с) под давлением Р (Па). На линиях притока и расхода устанавливают вентили, площади переходных сечений которых равны Апр и Ар, м2. Выходной величиной аппарата являются изменения давления Р, а входными переменными - изменение площадей А1, А2, и давления Рн.
Рис.10 Передаточные функции по каналам Z→Y, Xпр→Y, Xp→Y получаются в виде:
где R – газовая постоянная, Тг – абсолютная температура газа.
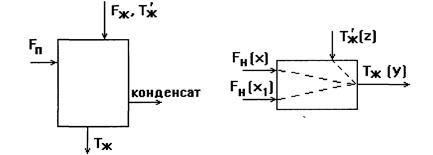
Пример 5. Теплообменник. Жидкий продукт нагревается насыщенным паром (расход - Fп, кг/с) до температуры Тж, °С. Расход продукта через теплообменник равен Fж, его температура на входе Т'ж, удельная теплоемкость Сж, Дж/(кг∙град). Выходной величиной теплообменника является изменение Тж, входные величины - изменение расхода пара Fп, расход жидкого продукта Рж, и его температура Тж. (рис. 11).
Рис.11
Передаточные функции теплообменника находятся в виде: по каналу X →Y
по каналу X1 → Y
по каналу Z → Y
где
Wж – масса жидкости в теплообменнике, кг, Wcт – масса теплопроводящих стенок, кг, А – суммарная поверхность стенок, м 2, Сст – теплоемкость стенок. Отсюда,
Если объект обладает запаздыванием, то коэффициенты Нк, Тк определяются по переходной функции, из которой выделено чистое запаздывание.
При расчете удобно пользоваться таблицей по форме:
3.2.5. Определение передаточной функции объекта методом площадей
Одним из наиболее удобных методов расчета передаточных функций по кривой разгона с использованием ЭВМ является метод "площадей". Рассмотрим функцию h(t), которая получена из экспериментальной Обычно выражение для передаточной функции ищут в виде одной из трех математических моделей:
Выражение
Очевидно, что для модели (47) a1 = S1, a2 = S2, а3 = S3; для модели (48) a1 = S1, a2 = S2; для модели (49) коэффициенты bi, ai, i = 1,2,3... связаны с коэффициентами Si системой уравнений
Коэффициенты Si связаны с переходной функцией h(t) соотношениями:
Моментом i - го порядка функции (1 - h(t)) называется несобственный интеграл
Тогда формулы для S можно переписать:
Таким образом, определив по графику h(t) значение моментов Mi методом численного интегрирования и вычислив величины Si, можно найти значения коэффициентов передаточной функции. Выбор вида передаточной функции производится из следующих соображений: если коэффициенты S1, S2, S3 положительны, то задаются моделью (47) или (48). Если хотя бы один из них отрицателен - моделью (49). Ниже приведен пример программы расчета значений коэффициентов Si, i = 1...4, составленной на алгоритмическом языке Бейсик [9]. В программе N - число координат передаточной функции; X -шаг Δt во времени; P(I) - значение ординат функции h(t). Вычисление моментов Mi, i = 0....3 производятся по дискретным значениям переходной функции по формулам трапеций.
010 READ N,X 020 DIM P[30] 030 DIM Z[30] 040 LET M0 = M1 = M2 = M3 = M4 = 0 050 FOR I = I TO N 060 READ P[I] 070 LET Z [I] = (1 - P[I]) ∙ X 080 LET M1 = M0 + Z[I] 090 LET T = (I-1)∙X 100 LET M1 =M1 + Z[I]∙T 110 LET M2 = M2 + Z[I] ∙ Т – 2 120 LETM3 = M3 + Z[I]∙T-3 130 NEXT I 140 LET S1 = M0-Z[I]/2 150 LET S2 = S1 - 2 - M1 160 LET S3 = S2 ∙ M0 - S1 ∙ M1 + M2 / 2 170 LET S4 = S3∙M0 - S2∙M1 + S1∙M2/2 - M3/6 180 PRINT " S1 = ", S1," S2 = ", S2 185 GOTO 190 190 PRINT " S3 = ", S3," S4 = ",S4 200 DATA 23,1 210 DATA 0,2.00000E - 02,.12,.24,.35,.45,.55,.62,.69,.76,.79 220 DATA.83,.87,.89,.92,.94,.95,.96,.97,.98,.99,.99, 1 230 END
READY Перед обращением к программе из экспериментальной кривой В заключение проверяется точность аппроксимации. Обычно принимают, что модель адекватна объекту, если разность между ординатами нормированных передаточных функций модели и объекта не превышает 0.05…0.07.
4. Выбор регулятора
4.1. Выбор типа регулирования
Тип регулирования выбирается с учетом свойств объекта и заданных параметров переходного процесса. К параметрам переходного процесса могут предъявляться различные требования. В одних случаях оптимальным является процесс с минимальным значением динамической ошибки, в других - с минимальным значением времени регулирования и т.д. Обычно выбирают один из трех типовых переходных процессов: граничный апериодический, с 20% перерегулированием, с минимальной квадратичной площадью отклонения. Граничный апериодический процесс характеризуется отсутствием перерегулирования, минимальным общим временем регулирования и наименьшим воздействием регулятора на объект (что вызывает наибольшее отклонение регулируемой величины от заданного значения). Такой переходный процесс используется в качестве оптимального при значительном влиянии регулирующего воздействия на другие технологические величины объекта, чтобы свести их отклонение к минимуму. Процесс с 20% перерегулированием характерен большей величиной воздействия регулятора и меньшим отклонением, при этом время регулирования несколько возрастает. Этот процесс выбирают в качестве оптимального, когда допустимо небольшое перерегулирование. Процесс с минимальной квадратичной площадью отклонения обладает значительным перерегулированием (до 40%), большим временем регулирования и наименьшей величиной динамической ошибки. Ориентировочно характер действия регулятора определяется по отношению запаздывания τ к постоянной времени объекта Т. При При При Более подробно вопрос выбора типа регулятора рассмотрен в [21], где приведены необходимые алгоритмы и таблицы.
4.2. Выбор закона регулирования
В зависимости от типа уравнения связывающего величину отклонения регулирующей величины ε(t) и перемещение регулирующего органа Y(t) различают следующие законы регулирования. Откуда
В этом случае характеристическое уравнение системы имеет вид:
На рис.43 приведены графики переходных процессов ПИ - регулятора (1) и регулятора Смита (2).
Рис.43
К недостаткам регулятора Смита, кроме сложности в его реализации, относится высокая чувствительность к параметрам настройки модели. Ошибки в настройке модели, вызванные неточными априорными знаниями о характеристиках объекта или нестационарностью его свойств, могут привести не только к ухудшению качества, но и к потере устойчивости. Теоретически запаздывание может быть скомпенсировано полностью введением в контур регулирования прогнозирующего звена с передаточной функцией еpΔt (рис.44).
Рис.44 В общем случае сигнал ошибки регулирования ε(t) содержит детерминированную Е(t) и случайную ξ(t) составляющие
Согласно теории фильтрации, можно построить фильтр, оптимальным образом выделяющий детерминированную составляющую из шума. Переходная функция такого фильтра [4]:
где Ве(jω), Bξ(jω) - энергетические спектры сигнала и шума. На выходе фильтра присутствует только детерминированная составляющая ошибки регулирования Е(t). Прогноз этой функции на время ΔT-E(t+ΔT). Изображение по Лапласу этих функций соответственно Z[E(t)], Z[(t+ΔT)]. Сдвиг функции по времени на AT соответствует умножению ее изображения на еpΔT, т.е.
Раскладывая ее в ряд Тейлора, имеем:
Переходя от изображения к оригиналам, получим:
Таким образом, будущее значение функции Е(t) связано с настоящими параметрами через взвешенную сумму производных. При отсутствии помех ( Структурная схема прогнозирующего фильтра изображена на рис.45.
Рис.45 Коэффициенты ri близки к коэффициентам ряда Тейлора. При медленных процессах Е(t) сложно реализовать аналоговые схемы вычисления производных Е(t). В этом случае целесообразно перейти от непрерывной функции к ее отсчетам в дискретные моменты времени, а производные заменить приращениями
Если использовать только первую производную, то прогнозируемое на ΔT значение функции будет равно:
Если использовать две производные, то
Прогнозируемая таким образом функция Е(t) будет дискретной. Если в контуре управления задействована ЭВМ, то численные результаты прогноза могут быть использованы непосредственно. Если же необходимо вернуться к аналоговой форме сигнала, то это можно сделать, используя интерполяционный ряд Котельникова [8].
Близкий к оптимальному результат дает применение цифроаналогового преобразователя с последующей низкочастотной фильтрацией. Операцию фильтрации сигнала при дискретном его представлении можно в первом приближении заменить операцией экспоненциального сглаживания [5]. Рассмотрим процесс, равный сумме постоянной а0 и случайного
где β – некоторый коэффициент < 1. Пусть ε(t) – ошибка прогноза Е(t).
Тогда
Прогноз в момент t является прогнозом, сделанным в момент времени (t -1), к которому добавляется последняя ошибка, умноженная на (1-β). Метод имеет два ценных свойства. Если β определено, то никаких значений о прошлом, за исключением величины, полученной в предыдущий момент времени, не требуется. И, второе, метод обладает свойством подстраивания к изменившимся условиям. Если истинное значение определяется линейной функцией а0+a1(t), то прогноз определяется формулами:
Оптимальный коэффициент β можно найти минимизируя по β сумму квадратов ошибки.
На практике ограничивают число членов ряда N и находят β методом последовательных приближений. В первом приближении
Экспоненциальное сглаживание дает несмещенную оценку математического ожидания.
S(t) является прогнозом на один шаг функции E(t). Процедуру получения S1 называют первым сглаживанием, S2 - второе сглаживание. Эту процедуру можно проводить несколько раз и обобщить на случай полиномиальных функций более высокого порядка. Задача фильтрации дискретной функции может быть решена и на основе теории цифровых фильтров. Математически работа линейного дискретного фильтра описывается разностным уравнением [20].
где Х(nТ), Y(nТ) – n-ые отсчеты входного и выходного сигналов, aj, bi – константы или отсчеты решетчатых функций, зависящих только от n. Коэффициенты aj, bi рассчитываются по заданной формуле частотной характеристики фильтра. Цифровые фильтры делятся на два класса: нерекурсивные и рекурсивные. Если в (112) все коэффициенты aj, то фильтр нерекурсивный. Алгоритм нерекурсивного фильтра
8. Микропроцессорные контроллеры для систем автоматизации
Микропроцессорные контроллеры предназначены для автоматизации непрерывных, непрерывно-дискретных и периодических технологических процессов. Контроллеры позволяют принимать и преобразовывать поступающую от датчиков контрольную информацию, вырабатывать управляющие (командные) воздействия и осуществлять взаимодействие и обмен информацией с оператором технологического объекта управления (ТОУ). Серийно выпускаемые отечественные контроллеры для систем автоматизации по функциональному назначению делят на три класса: регулирующие микропроцессорные контроллеры (ремиконты), логические микропроцессорные контроллеры (ломиконты) и дисплейные микропроцессорные контроллеры (димиконты) [6, 19].
8.1. Ремиконты
Эти контроллеры предназначены для автоматизации ТОУ с несколькими регулируемыми координатами. В класс ремиконтов входят контроллеры Р-100, 110, 112, 120, 122 и 130. Базовым контроллером для данного класса является ремиконт Р-100. Остальные модификации контроллеров имеют в значительной мере аналогичную структуру, модульную и элементную базу. Ремиконт Р-100. Контроллер представляет собой проектно-компонуемое устройство, состоящее из постоянной и переменной частей. В первую часть входят неизменяемый комплект технических устройств, аппаратуру переменной части компонуют в соответствии с характеристиками ТОУ, в частности числом каналов ввода-вывода информации и контуров регулирования.
Рис. 46. Техническая структура ремиконта Р100
Техническая структура ремиконта Р-100 представлена на рис. 46. В постоянную часть контроллера (ПК) входит ряд модулей базового комплекта: процессор (ПРЦ), оперативное запоминающее устройство (ОЗУ) емкостью 2 Кбайта, три постоянных запоминающих устройства (ПЗУ) емкостью 8 Кбайт каждое, индикатор (МИН), сигнализатор отказов (МСО) и усилитель мощности (УМ). С ПК информационно связана панель оператора (НПО), используемая для настройки контроллера. Модуль ПРЦ построен на базе микропроцессора серии К580. Он осуществляет управление работой всех блоков Р-100 и обработку информации в соответствии с заданной программой. В модулях ПЗУ.1 и ПЗУ.2 „зашито” программное обеспечение контроллера, включающее следующие программы: организации процесса вычислений, регулирования, обслуживания панели оператора и внешних устройств, тестирования и самодиагностики. В модуле ОЗУ хранят информацию, которую может изменять оператор. Сюда относят характеристики алгоритмов регулирования, параметры конфигурации контуров регулирования и режимов их функционирования, настроечные коэффициенты, значения заданий, длительности циклов и т.д. В этом модуле хранят информацию, накапливающуюся в процессе реализации алгоритмов регулирования. Для сохранения запрограммированной и накапливающейся в ОЗУ информации при аварийном отключении сетевого питания автоматически подключают батарею сухих элементов. Модули ПЗУ.3 и УМ предназначены для обслуживания панели оператора ПНО. В ПЗУ.3 „зашита” программа обслуживания, а УМ усиливает интерфейсные сигналы по мощности и позволяет подключать ПНО через кабель длиной до 3 м. Модуль МСО сигнализирует о наличии характерных отказов, выявляемых с помощью программ диагностики, и дистанционно передает сообщение о выявленных нарушениях в работе ремиконта. Модуль МИН выполняет сервисные функции. Он позволяет с помощью светодиодов избирательно контролировать сигналы на входах-выходах контроллера. Проектно-компонуемый комплект (ПРК) содержит модули УСО следующих модификаций: аналого-цифрового преобразователя (АЦП) на 16 аналоговых входов (до 4 модулей); гальванического разделителя (РГ1) на 8 аналоговых входов (до 6 модулей); цифро-аналогового преобразователя (ЦАП) на 8 входных аналоговых сигналов (до 8 штук); выходных гальванических разделителей (РГ2) на 4 аналоговых выхода (до 6 модулей); дискретно-цифрового преобразователя (ДЦП) на 16 дискретных входных сигналов (до 8 штук); цифро-импульсного преобразователя (ЦИП) на 8 выходов для ввода импульсных дискретных 1 сигналов (до 8 штук). Модули и устройства постоянной и проектно-компонуемой частей ремиконта Р-100 связаны между собой шиной внутриблочной интерфейсной связи (ШИС). Программно-алгоритмическое обеспечение ремиконта Р-100. Функциональные возможности контроллера определяют программы, помещенные в ПЗУ. Программное обеспечение позволяет абстрагироваться от физических элементов, образующих контроллер. Оно выполнено таким образом, что физическая структура представляется в виде виртуальной (кажущейся), подобной структурам обычных устройств автоматического регулирования и управления. Основу виртуальной структуры образуют следующие пять областей (рис.47): ввода информации, вывода информации, управления, алгоритмических ресурсов и связи с оператором.
Рис. 47. Виртуальная структура реинконта Р100 Области ввода и вывода информации предназначены для подключения соответственно датчиков и исполнительных устройств. Входы рассчитаны на работу с унифицированными аналоговыми (напряжение 0-10 В, ток 0-5 мА, 0-20 мА, 4-20 мА) и дискретными (0 или 24 В постоянного тока) сигналами. На выходах формируются унифицированные аналоговые сигналы, а также дискретные и импульсные сигналы типа „сухой контакт”. Область управления предназначена для обработки поступающей информации и состоит из 64 алгоритмических блоков (алгоблоков): 1.1, 1.2,..., 8.8. Функции алгоблоков заранее не определены - в процессе технологического программирования оператор может „заполнить” каждый алгоблок любым алгоритмом из числа входящих в библиотеку алгоритмов контроллера. Типовой алгоблок (рис.48) содержит программно реализованные задатчик (ЗДН), переключатель режимов работы (ПР) и орган ручного управления (РУЧ). Каждый алгоблок имеет восемь входов (x1.., x8), а также один аналоговый (у) и два дискретных (z1, z2) выхода, которые в исходном состоянии не запрограммированного ремиконта ни с чем не связаны. Назначение входов определено алгоритмом, который помещен в алгоблок; при этом часть входов может быть аналоговыми, а часть -дискретными. Назначение выходов также определено алгоритмом, реализуемым ремиконтом.
Рис.48. Функциональная схема алгоблока ремиконта Р100
Таблица 3. Библиотека алгоритмов ремиконта Р-100
Алгоритмическая часть ремиконта Р-100 образована библиотекой алгоритмов, набором связей (конфигурацией) и набором коэффициентов. Библиотека алгоритмов представляет собой набор из 25 программных модулей (табл.3), предназначенных для решения наиболее часто встречающихся задач автоматического регулирования ТОУ. Система связей алгоблоков между собой и входами-выходами ремиконта образует конфигурацию контроллера. При конфигурировании контроллера для конкретной АСР оператор соединяет входы алгоблока с любыми нужными входами или выходами других алгоритмических блоков, а выходы данного алгоблока коммутирует с выходами или задатчиками других блоков. Таким образом, в процессе конфигурирования оператор объединяет алгоблоки во взаимосвязанные группы, образующие нужные законы регулирования. Конфигурационные возможности ремиконта Р-100 позволяют создавать каналы регулирования, состоящие из разного числа алгоблоков, включенных параллельно, последовательно или с применением смешанного соединения. Например, каждый канал регулирования может состоять из одного алгоблока, в который помещен ПИД-алгоритм; один канал может состоять из 64 алгоблоков. Однако более типично использование в контроллере 8-16 каналов, каждый из которых содержит от 1 до 4 алгоблоков. По дискретным командам указанные каналы можно безударно включать и отключать, переходить с одного из них на другой, запрещать изменение значений выходных сигналов в том или ином направлении, изменять режимы их работы. Для настройки алгоблоков и контроля за их работой используют панель оператора ПНО, которую подключают к контроллеру через разъем. При конфигурировании оператор устанавливает на ПНО номер алгоблока; выбирает из библиотеки требуемый алгоритм регулирования; устанавливает нужную конфигурацию, определяющую связи входов и выходов алгоблока, коэффициенты и значение сигнала задания ПНО; выбирает режим работы. В общем случае каждый алгоблок может работать в одном из семи режимов: автоматическом (АВТ), каскадном (КАСК), супервизорном (УВМ), ручном (РУЧН), дистанционном (ДИСТ), запрета (ЗАПР), слежения (СЛЕЖ). В режимах АВТ, КАСК, УВМ (см. рис.6.3) алгоритм включен в действие и выполняет предписанную ему функцию, формируя аналоговый или дискретный сигнал на выходе алгоблока. При этом ключ Кпр коммутирует соответственно один из каналов АВТ, КАСК, УВМ, а ключ Кв отсоединяет орган ручного управления РУЧ. В остальных режимах алгоблок отключен, и связь между аналоговыми выходами алгоритма и алгоблока отсутствует. В режиме АВТ программный задатчик ЗДН подключен к ПНО, с клавиатуры которой оператор изменяет сигнал значения. В режиме КАСК задатчик ЗДН отключен от ПНО и соединен с выходом другого ведущего алгоблока ВДЩ, если такая связь задана в процессе конфигурирования контроллера. В режиме УВМ к задатчику подключен выходной сигнал УВМ, который изменяет величину задания. В режиме РУЧН, устанавливаемом оператором с помощью клавиатуры ПНО, к аналоговому выходу алгоблока Кв подсоединяется программный узел РУЧ; при этом ключ Кпр коммутирует канал АВТ. Сигнал ручного управления задает оператор посредством клавиатуры ПНО. Режим ДИСТ (рис.49, а)устанавливают с помощью дискретной команды Хд, подаваемой на один из входов алгоблока А. В этом режиме аналоговый выход у алгоблока подключен ко входу хвх алгоблока.
Рис. 49. Схемы включения алгоблока в различных режимах управления: а - дистанционном; 6 - запрета; в - слежения.
Режим ЗАПР (рис.49, б) также устанавливают дискретным сигналом хз, подаваемым на вход алгоблока А. В этом режиме выходной сигнал У фиксируют на некотором уровне или обращают в нуль, в зависимости от вида запрета. Режим СЛЕЖ (рис.49, в) предусмотрен только в алгоблоках, работающих в качестве ведущих в каскадных схемах. Ведущий алгоблок ВДЩ переходит в режим СЛЕЖ в том случае, когда ведомый алгоблок ВДМ выходит из режима КАСК. В режиме СЛЕЖ реализуют „обратный счет”: выходной сигнал ведущего алгоблока отслеживает сигнал задания ведомого алгоблока. К числу распространенных алгоритмов относят алгоритм РАС (01)-регулирование аналоговое стандартное по ПИД-закону. Структурная схема алгоритма РАС (01) показана на рис. 50.
Рис. 50. Функциональная схема алгоритма регулирования аналогового стандартного по ПИД – закону.
В алгоритме РАС (01) входные сигналы x1-х3суммируются с некоторыми весами k1-k3 на сумматоре Σ1, проходят через экспоненциальный фильтр с постоянной времени Тф и объединяются на сумматоре Σ3 с переменной k4 x4+k5 x5, получаемой на элементе Σ2. К сумматору Σ3 подведено задание хздн. Получаемое в Σ3 рассогласование с вводят в усилитель с зоной нечувствительности А, инвертированный выход которого используют для вычисления регулирующего воздействия у в соответствии с передаточной функцией ПИД-закона:
На выходе ПИД-звена предусмотрен программный ограничитель с предельными значениями Н1 и Н2. При достижении сигналом у0 граничного значения интегрирование в ПИД-звене прекращается, и выходной сигнал интегратора фиксируется на данном уровне. Алгоритм РАС (01) содержит программный нуль-орган с границей Н3 и гистерезисом Н4, контролиру
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 221; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.148.222 (0.012 с.) |

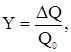
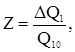
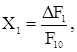
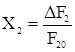 .
.
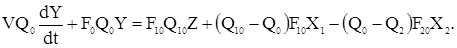
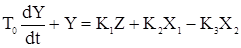 ,
,
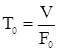 - постоянная времен и объекта,
- постоянная времен и объекта,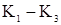 - коэффициенты усиления по каналам,
- коэффициенты усиления по каналам,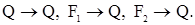
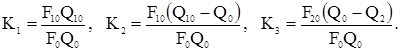
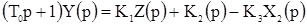
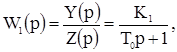
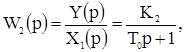
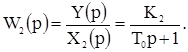
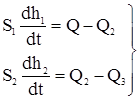
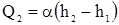 получим
получим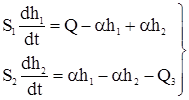
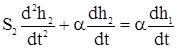
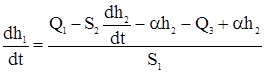
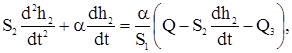
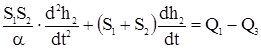 .
.
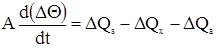 ,
,
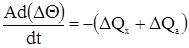 .
.
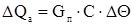 ,
,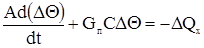 .
.
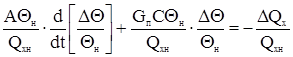 ,
,
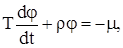
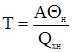 – постоянная времени, в минутах,
– постоянная времени, в минутах,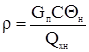 – степень самовыравнивания,
– степень самовыравнивания,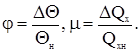
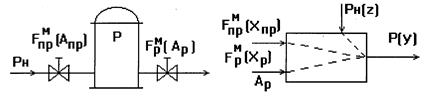
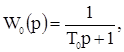
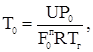
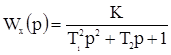 .
.
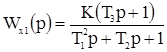 .
.
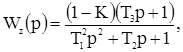
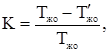
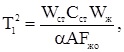
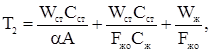
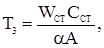

 .
.



 , обратное передаточной функции модели, можно разложить в ряд по степени р
, обратное передаточной функции модели, можно разложить в ряд по степени р

 ,
,
 ,
,
 ,
,
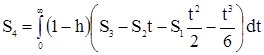 .
.
 .
.
 ,
,
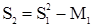 ,
,
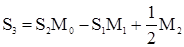 ,
,
 .
.
 выбирается позиционное регулирование.
выбирается позиционное регулирование. выбирается непрерывное регулирование, либо импульсное.
выбирается непрерывное регулирование, либо импульсное. применяют многоконтурные системы регулирования и принимают меры по компенсации влияния запаздывания.
применяют многоконтурные системы регулирования и принимают меры по компенсации влияния запаздывания.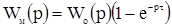 .
.
 .
.


 .
.
 .
.
 .
.

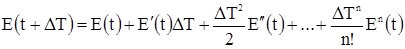 .
.
 ) и при бесконечной дифференцируемости процесса бесконечный ряд Тейлора для этого процесса является оптимальным оператором прогнозирования на любой интервал времени ΔT, независимо от вида энергетического спектра сигнала.
) и при бесконечной дифференцируемости процесса бесконечный ряд Тейлора для этого процесса является оптимальным оператором прогнозирования на любой интервал времени ΔT, независимо от вида энергетического спектра сигнала.

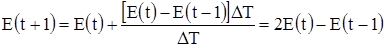 .
.

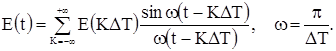
 ,
,


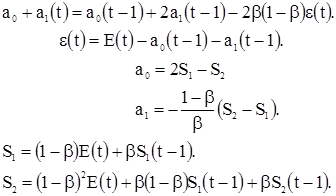
 .
.
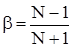 .
.
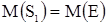 .
. ,
,
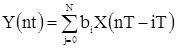 .
.





 .
.



