
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип відповідності. Переваги і недоліки теорії Бора.Содержание книги
Поиск на нашем сайте
Головна відмінність квантової теорії від класичної лежить в припущенні дискретності станів різних фізичних систем. Істотно, що при тих умовах, коли вказана дискретність станів сглажена, там виникає співпадання висновків обох теорій. Наприклад, спектральні закономірності атомів при великих значеннях головного квантового числа п однаково можна описати як квантовою так і класичною теорією. Класичні уявлення виникли при описі різноманітних закономірностей в макросистемах, де дискретність практично не проявляється. Наприклад, різниця моментів кількості руху в суміжних квантових станах рівна При обертання 1об/сек. (кутова швидкість Тобто азимутальне квантове число Отже, величина В мікросистемах різниця значень величини в сусідніх квантових станах майже рівні самим величинам, тому дискретність їх, незважаючи на свою малість в макросистемах, являється дуже суттєвою в мікросистемах. Таким чином,квантова теорія Бора не відкидає закономірності старої класичної теорії, але уточнює їх, враховуючи дискретність станів. Положення про включення старої теорії в нову, про перехід некласичної теорії в граничному випадку в класичну, становить зміст принципу відповідності теорій, які заміняють одна одну. Переваги теорії Бора: 1. Показала непридатність класичних законів для пояснення фізичних процесів мікросвіту, де головну роль відіграють квантові закони. 2. Стимулювала розвиток експериментальних робіт в області фізики атома. 3. Створила основи нової спеціальності в фізиці – атомної спектроскопії. Недоліки теорії Бора: 1. Теорії Бора властива певна неоднозначність. Вона є не послідовно класичною, і не послідовно квантовою теорією. 2. Навіть для найпростіших атомів теорія давала розподіл частот, але не інтенсивностей. 3. Повна невдача при спробі скласти теорію наступного за атомом водню – атома гелію. 4. Неможливість пояснення хвильових властивостей часток.
В даний час теорія Бора має евристичне значення і є перехідним етапом для створення послідовної теорії атомних явищ. 1.12. Атомний за лишок, поляризуємість багатоелектронних атомів Розрахунок енергетичних рівней атома з великою кількістю електронів представляє собою дуже складну задачу, яка вирішується наближенно методами квантової механіки. З точки зору квантової теорії побудова спектра гелія вже являється задачею без розв’язку, так як і для класичної механіки. Однак є група елементів, спектроскопічні властивості яких пояснюються напівкількісно в рамках теорії Бора-Зоммерфельда. Це відноситься до елементів Li (Z=3); Na (Z=11); K Рис. 1.20 електронів утворює компактну систему з загальним зарядом + е - “атомний залишок” - аналогічно протону у водня. “Зовнішній” електрон рухається в полі атомного залишку подібно до атому водню. При великих n, поле залишка майже Кулонівське і для далеких орбіт значення енергій атомів лужних металів можуть бути визначені по аналогу атома водню:
тобто рівні будуть воднеподібними і виродженими по азімутальному квантовому числу. Для орбіт близьких до атомного залишку, поле буде відрізнятися від Кулонівського. Причини: 1)Зовнішній електрон, знаходячись на відстані r від атомного залишку своїм кулонівським полем
де Потенціальна енергія електрона
Це означає, що силове поле в якому рухається електрон, вже не чисто Кулонівське. 2)Друга причина полягає в проникненні окремих ділянок траекторії руху зовнішнього електрона в середину атомного залишку. Таким чином ці причини приводять до пониження енергетичних рівнів спектрів лужних металів відносно рівнів водня, тоді вираз для енергії можна записати
де R – постійна Рідберга; с – Швидкість світла; n – головне квантове число Для кожного значення k, буде своя поправка Δ(s, p, d, f…), яка зменшується з збільшенням k і яку з загальному випадку позначають Δ. Наприклад для атома Na при k=4 ® Δ=0; k=3® Δ=0,01; k=2® Δ=0,86; k=1® Δ=1,35. Тоді згідно комбінаційного принципу в спектрах атомів лужних металів будуть спостерігатися лінії різних серій з хвильовими числами
Причому в (3.4) можливі тільки комбінації переходів при Δk=±1. Тоді в спектрі можна виділити чотири серії, з врахуванням, що для лужних металів (Na, K) основний стан для зовнішнього електрона 3S. 1. Головна (від латинського “principale” - головна) серія з хвильовими числами, які відповідають переходам: 2. Різка (“sharp” - різка) серія: 3. Дифузна (“diffuse” - розмита) серія: 4. Основна (“fundamental” - основна або фундаментальна): Детальне експериментальне дослідження спектрів атомів лужних металів показує наявність дублетної структури у ліній головної і різкої серій і триплетної - у дифузної і основної. Таку структуру спектрів можна пояснити, якщо припустити наявність двох близьких енергетчних рівнів у кожного з P, D, F-рівней, а S-рівні залишити одиночними. Це означає, що введена поправка Δ в (3.4) для кожного випадка p, d, f … повинна приймати два близьких значення, що потребує вияснення можливої причини такого припущення. Спін електрона Так як кожна поправка p, d, f … має два близьких значення, то відповідно, енергія в цих станах буде відповідати виразам:
Але у Е1 і Е2, головне квантове число n і азімутальні квантові числа nj=k однакові, це означає, що різниця в енергії може бути викликана тільки різницею в якомусь третьому квантовому числі. Що це за число? Пояснення було дано Гаудсмітом і Уленбеком (амер. вчені) у 1925 р., які висунули гіпотезу про обертання електрона навколо власної вісі. Тоді він повинен мати власний механічний момент, кількість руху Ps, але так як це заряджена частинка,то і деякий магнітний момент ms - “спін” (обертання). За квантовою теорією
Магнітне поле орбітального руху електрона Норб створює переважний напрямок, по відношенню до якого вектор момента кількості руху спіна електрона може розташовуватися під (2|S|+1) дискретними кутами. Маємо аналог магнітного диполя в неоднорідному магнітному полі (електрон з власним магнітним моментом в магнітному полі орбітального руху). Тоді електрон повинен мати магнітну енергію msНсosQ. Різні значення цієї енергії викликає розщеплення ліній на (2|S|+1) рівнів. Експериментально визначено що розщеплення дорівнює 2, тоді величині спінового квантового числа треба приписати значення ½, тобто прийняти, що
і припустити можливість лише двоякої орієнтації спіна електрона відносно нормалі до площини орбіти: паралельно і антипаралельно. Але S-рівні не розщеплюються, тому Уленбек і Гаудсміт припустили, що механічний і магнітний моменти орбітального руху еле-трона пропорційні не азімутальному числу k, а числу l на одиницю менше k- l=0,1,2…(к-1)- орбітальне квантове число. Тоді у S-рівня k=1, відповідно l=0 і pl і ml немає, додаткової магнітної енергії немає, тобто розщеплення не відбувається. Як наслідок, гіпотеза Гаудсміта і Улембека, що пояснює наявність дублетів і триплетів в спектрах лужних металів складається з трьох частин: 1. Припущення про наявность у електрона власних механічного і магнітного моментів pS, mS (спін електрона). 2. Припущення, що величина механічного момента 3. Припущення про заміну азимутального квантового числа k, як міри механічного і магнітного моментів орбітальоного руху електрона, на орбітальне квантове число l= k-1.
Таким чином, враховуючи спін електрона, стан атомів лужних металів необхідно характеризувати 3-ма квантовими числами: n, l, s(±1/2) (при відсутності зовнішньої дії).
Рис. 1.21
1.14. Векторна модель атома Наявність спіна електрона і введення орбітального квантового числа приводять до ускладнення моделі атома. Спеціфічний рух електрона (по орбіті і власне обертання) можна описати двома моментами кількості руху: орбітальним
Тоді загальний момент (повний момент є вектор) буде
і для квантових чисел у вигляді векторів маємо
де j- внутрішнє квантове число, що характеризує повний механічний момент електрона в атомі (атом одноелектронний). Правило відбору для даного квантового числа
Тепер в символічних позначеннях квантових станів атомів недостатньо вказати тільки на n - головне квантове число і орбітальне квантове число - l. Внутрішнє квантове число вказують зправа внизу і значення його згідно (1.75) Таблиця 3.
З врахуванням правила відбору Dj=0,±1, у Na для дифузної серії mD÷3P (m=3,4…) замість квартетів маємо триплети. Гіпотеза Гаудсміта і Уленбека повністю пояснює дослід Штерна і Герлаха: атоми срібла знаходяться в S-стані (l=0), це означає, що орбітальний механічний момент кількості руху Pl і магнітний момент ml дорівнюють нулю, але повний магнітний момент атома Pj¹0, а дорівнює спіновому магнітному моменту, який може орієнтуватися паралельно або антипаралельно до зовнішнього поля, відповідно пучок розщеплюється на два, а не на три. Крім того, в досліді було показано, що відхилення пучка відповідає значенню магнітного момента рівному одному магнетону Бора mБ, тобто спіновий магнітний момент електрона дорівнює магнетону Бора
а спіновий механічний момент кількості руху
Для відношення орбітальних моментів
де Ефект Зеемана. Якщо розмістити джерело лінійчатого спектра випромінювання в сильне магнітне поле, то крім ліній з частотою νоі в спектрі спостерігаються дублети з частотами (νоі + Δν) і (νоі – Δν) при спостереженні паралельно напрямку вектора індукції магнітного поля і триплети ліній з частотами (νоі + Δν), νоі, (νоі – Δν) при спостереженні перпендикулярно до поля. Вказане розщеплення спектральних ліній джерела випромінювання було відкрито в 1896р. голландським вченим Зееманом (1865–1943) і носить назву нормального ефекту Зеемана. Розглянемо коротко теорію ефекту Зеемана в рамках електронної і квантової теорій. 1. Електронна теорія нормального ефекта Зеемана була запропонована Лоренцом (1853–1928), голландським фізиком, у 1896р. Дана теорія основана на розкладанні орбітального руху електрона, який представлений гармонічним коливанням з амплітудою Е0, на два лінійних гармонічних коливання по двом взаємоперпендикулярним напрямкам з частотою n0 і амплітудою El, Et, з яких
яка має ненульове значення для компоненти руху електрона ^ магнітному полю, тобто для Et і відповідно для двох колових рухів. Наявність Fл при
де При накладанні магнітного поля зміниться доцентрова сила для колових рухів внаслідок додавання сили Лоренца. Тоді умова механічної стійкості атома для правого і лівого кола буде:
З врахуванням, що
|
||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 222; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.227.3 (0.01 с.) |

 , а сам момент кількості руху макроскопічного тіла
, а сам момент кількості руху макроскопічного тіла  . Оцінимо
. Оцінимо  для невеликої краплі води діаметром 0,1 мм. момент інерції
для невеликої краплі води діаметром 0,1 мм. момент інерції 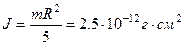 .
. ), то вона має момент кількості руху
), то вона має момент кількості руху 
 .
. (Z=19); Rb (Z=37); Cs (Z=55). Чим характерні ці атоми, - вони складаються з ядер з зарядом +Ze, групи із (Z-1) електронів, які рухаються відносно близько до ядра і одного електрона, який рухається поза цієї групи. Наприклад, Li- ядро і група (Z-1)
(Z=19); Rb (Z=37); Cs (Z=55). Чим характерні ці атоми, - вони складаються з ядер з зарядом +Ze, групи із (Z-1) електронів, які рухаються відносно близько до ядра і одного електрона, який рухається поза цієї групи. Наприклад, Li- ядро і група (Z-1)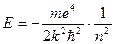 , (1.68)
, (1.68) викликає поляризацію атомного залишкуі створює у нього електричний дипольний момент
викликає поляризацію атомного залишкуі створює у нього електричний дипольний момент ,
, - поляризуємість. Напрямок
- поляризуємість. Напрямок 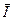 буде завжди співпадати з миттєвим значенням радіус вектора електрон-атомного залишка, тобто переважного напрямку не буде.
буде завжди співпадати з миттєвим значенням радіус вектора електрон-атомного залишка, тобто переважного напрямку не буде. буде складатися з потенціальної енергії
буде складатися з потенціальної енергії  в Кулонівському полі залишка і потенціальної енергії
в Кулонівському полі залишка і потенціальної енергії  в полі дипольного моменту атомного залишка
в полі дипольного моменту атомного залишка . (1.69)
. (1.69) , (1.70)
, (1.70)
 , (1.71)
, (1.71) .
. .
. .
.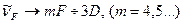 .
.
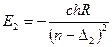 . (1.72)
. (1.72)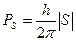 , а ms~mБ ® ms=ms·mБ. (1.73)
, а ms~mБ ® ms=ms·mБ. (1.73)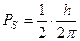 , (1.74)
, (1.74) , тобто дорівнює половині елементарного момента руху.
, тобто дорівнює половині елементарного момента руху. Тоді магнітне квантове число m, що характеризує проекцію орбітального механічного момента на переважний напрямок дії зовнішньої сили може приймати значення від l до –l, тобто
Тоді магнітне квантове число m, що характеризує проекцію орбітального механічного момента на переважний напрямок дії зовнішньої сили може приймати значення від l до –l, тобто  .
. і власним механічним рухом електрона
і власним механічним рухом електрона  . Але кожне з цих рухів має і відповідний механічний момент, взаємодія цих магнітних моментів приводить до визначеної орієнтації механічних моментів
. Але кожне з цих рухів має і відповідний механічний момент, взаємодія цих магнітних моментів приводить до визначеної орієнтації механічних моментів 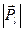 і
і  в просторі, утворенню загального механічного момента
в просторі, утворенню загального механічного момента  і прецесії навколо даного момента. При цьому, число можливих проекцій моментів
і прецесії навколо даного момента. При цьому, число можливих проекцій моментів  і
і  по відношенню до загального момента
по відношенню до загального момента 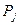 визначається через відповідні магнітні квантові числа (орбітальне ml і спінове mS):
визначається через відповідні магнітні квантові числа (орбітальне ml і спінове mS):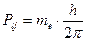 і
і  .
. ,
, , (1.75)
, (1.75) (1.76)
(1.76) .
. ;
;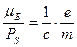 (гіромагнітне відношення).
(гіромагнітне відношення). , тобто
, тобто , (1.77)
, (1.77) і
і 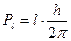 . З (1.77) випливає, що гіромагнітне відношення власного моменту в 2 раза більше ніж для орбітального.
. З (1.77) випливає, що гіромагнітне відношення власного моменту в 2 раза більше ніж для орбітального. çç
çç  , а
, а  ^
^  і частотою n0 в площині ^ до напрямку ліній індукції магнітного поля
і частотою n0 в площині ^ до напрямку ліній індукції магнітного поля  , (1.78)
, (1.78) буде приводити до зміни швидкості колових обертань електрона. Це в свою чергу викличе зміну величин, що входять в умову механічної стійкості електрона в атомі. При
буде приводити до зміни швидкості колових обертань електрона. Це в свою чергу викличе зміну величин, що входять в умову механічної стійкості електрона в атомі. При  дана умова має вигляд
дана умова має вигляд , (1.79)
, (1.79)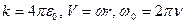 ,
,  - колова частота електрона за відсутності магнітного поля.
- колова частота електрона за відсутності магнітного поля. . (1.80)
. (1.80) рівняння (1.80) можна переписати в наступному вигляді:
рівняння (1.80) можна переписати в наступному вигляді: . (1.81)
. (1.81)


