
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Меры центральной тенденции: мода, медиана, среднее. Преимущества и
Ограничения мер центральной тенденции. Отношения между мерами центральной Тенденции в разных видах распределения. В статистике под рядом распределения понимают распределение частот по вариантам. Измеренные величины признака в вы Если по оси абсцисс — ОХ откладывать величины классовых интервалов, а по оси ординат — OY величины частот, попадающих в данный классовый интервал, то получается так называемая гистограмма распределения частот. При этом над каждым классовым интервалом строится колонка или прямоугольник, площадь которого оказывается пропорциональной соответствующей частоте. Гистограмма представляет собой графическое изображение данного частотного распределения. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ РАСПРЕДЕЛЕНИЙ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ Для экспериментальных данных, полученных по выборке, можно вычислить ряд числовых характеристик (мер). Мода Числовой характеристикой выборки, как правило, не требующей вычислений, является так называемая мода. Мода — это такое числовое значение, которое встречается в выборке наиболее часто. Мода обозначается иногда как Так, например, в ряду значений (2, 6, 6, 8, 9, 9, 9, 10) модой является 9, потому что 9 встречается чаще любого другого числа. Обратите внимание, что мода представляет собой наиболее часто встречающееся значение (в данном примере это 9), а не частоту встречаемости этого значения (в данном примере равную 3). Моду находят согласно следующим правилам: 1) В том случае, когда все значения в выборке встречаются одинаково часто, принято считать, что этот выборочный ряд не имеет моды. Например: 5, 5, 6, 6, 7, 7 — в этой выборке моды нет. 2) Когда два соседних (смежных) значения имеют одинаковую частоту и их частота больше частот любых других значений, мода вычисляется как среднее арифметическое этих двух значений. Например, в выборке 1, 2, 2, 2, 5, 5, 5, 6 частоты рядом расположенных значений 2 и 5 совпадают и равняются 3. Эта частота больше, чем частота других значений 1 и 6 (у которых она равна 1).
Следовательно, модой этого ряда будет величина 3) Если два несмежных (не соседних) значения в выборке имеют равные частоты, которые больше частот любого другого значения, то выделяют две моды. Например, в ряду 10, 11, 11, 11, 12, 13, 14, 14, 14, 17 модами являются значения 11 и 14. В таком случае говорят, что выборка является бимодальной. Могут существовать и так называемые мультимодальные распределения, имеющие более двух вершин (мод). 3) Если мода оценивается по множеству сгруппированных данных, то для нахождения моды необходимо определить группу с наибольшей частотой признака. Эта группа называется модальной группой. Медиана Медиана — обозначается Задача 4.1. Найдем медиану выборки: 9, 3, 5, 8, 4, 11, 13. Решение. Сначала упорядочим выборку по величинам входящих в нее значений. Получим: 3, 4, 5, 8, 9, 11, 13. Поскольку в выборке семь элементов, четвертый по порядку элемент будет иметь значение большее, чем первые три, и меньшее, чем последние три. Таким образом, медианой будет четвертый элемент — 8. Задача 4.2. Найдем медиану выборки: 20, 9, 13, 1, 4, 11. Упорядочим выборку: 1, 4, 9, 11, 13, 20. Поскольку здесь имеется четное число элементов, то существует две «середины» — 9 и 11. В этом случае медиана определяется как среднее арифметическое этих значений.
Среднее арифметическое ряда из
Здесь величины 1, 2...п являются так называемыми индексами. В том случае, если отдельные значения выборки повторяются
в таком случае называют взвешенной средней, где Знак
Например, в формуле (4.1) суммирование начинается с первого элемента выборки, поэтому и пишется так: Если же мы запишем так: В дальнейшем мы будем пользоваться сокращением, которое состоит в том, что если производится суммирование всех элементов выборки от первого до последнего, то верхний и нижний пределы суммирования указываться не будут, а пишется просто:
При вычислении величины средней по таблице чисел в дальнейшем будет использоваться следующая формула:
где при этом индекс Тогда Символическое обозначение Символ Следует подчеркнуть, что средние величины характеризуют выборку одним (средним) числом. Преимущество, или иначе, информативная значимость, средних величин заключается в их способности аккумулировать или уравновешивать все индивидуальные отклонения, в результате чего проявляется то наиболее устойчивое и типичное, что характеризует качественное своеобразие варьирующего объекта, позволяя отличить одну выборку от другой, а на этой основе, например, одно измеренное психологическоесвойство от другого. Однако среднее как статистический показатель не лишено недостатков. Так, например, при вычислении среднего количества ошибок при выполнении корректурной пробы может быть получена величина равная 1,3 ошибки или при определении среднего числа учеников, обучающихся в пятых классах данной школы, может быть получена величина равная 30,07. Конечно, с точки зрения статистика эти величины обычны, но для психологических задач они могут быть неприемлемы. Кроме того, среднее оказывается достаточно чувствительным к очень маленьким или очень большим величинам, отличающимся от основных значений измеренных характеристик. Приведем пример из книги Дж. Б. Мангейма и Ричарда К. Рича: «Политология. Методы исследования» М., 1997 г. «Пусть 9 человек имеют доход от 4500 до 5200 тыс. долларов в месяц. Величина их среднего дохода равняется 4900 долларов. Если же к этой группе добавить человека, имеющего доход в 20000 тыс. долларов в месяц, то средняя всей группы сместится и окажется равной 6410 Долларов, хотя никто из всей выборки (кроме одного человека) реально не получает такой суммы. Понятно, что аналогичное смещение, но в противоположную сторону можно получить и в том случае, если добавить в эту группу человека с очень маленьким годовым доходом».
Важно подчеркнуть, что подобные крайние величины, т. е. те, которые существенно искажают величину средней, оказываются в то же время и наименее характерными для изучаемой генеральной совокупности. Именно поэтому в статистике, кроме средней величины, используются и другие характеристики «типичных значений» выборки, такие, как мода, медиана и ряд других характеристик. 4.4. Разброс выборки Разброс (иногда эту величину называют размахом) выборки обозначается буквой R. Это самый простой показатель, который можно получить для выборки — разность между максимальной и минимальной величинами данного конкретного вариационного ряда, т. е.
Понятно, что чем сильнее варьирует измеряемый признак, тем больше величина R, и наоборот. Однако может случиться так, что у двух выборочных рядов и средние, и размах совпадают, однако характер варьирования этих рядов будет различный. Например, даны две выборки: X = 1040
При равенстве средних и разбросов для этих двух выборочных рядов характер их варьирования различен. Для того чтобы более четко представлять характер варьирования выборок, следует обратиться к их распределениям. 4.5. Дисперсия Рассмотрим еще одну очень важную числовую характеристику выборки, называемую дисперсией. Дисперсия представляет собой наиболее часто использующуюся меру рассеяния случайной величины (переменной). Дисперсия это среднее арифметическое квадратов отклонений значений переменной от её среднего значения.
где п — объем выборки — индекс суммирования
Вычислим дисперсию следующего ряда Прежде всего найдем среднее ряда (4.5). Оно равно Рассмотрим величины:
Так образуется новый ряд чисел. Его особенность в том, что Получить полный текст Отметим, что сумма такого ряда Для того чтобы избавиться от нуля, каждое значение разности
Это и есть искомая дисперсия. Общий алгоритм вычисления дисперсии для одной выборки следующий: 1. Вычисляется среднее по выборке. 2. Для каждого элемента выборки вычисляется его отклонение от средней, т. е. получается множество Т. 3. Каждый элемент множества Т возводят в квадрат. 4. Находится сумма этих квадратов. 5. Эта сумма, как и в случае вычисления среднего, делится на общее количество членов ряда — п. В ряде случаев, особенно когда величина выборки мала, деление осуществляется не на величину п, а на величину п —1. Величина, получающаяся после пятого шага, и есть искомая дисперсия. Расчет дисперсии для таблицы чисел осуществляется по формуле 4.6:
где индекс j меняется от 1 до р, где р число столбцов в таблице, а индекс
N — общее число всех элементов в таблице (анализируемой совокупности экспериментальных данных) и в общем случае N = Дисперсию для генеральной совокупности принято обозначать как Преимущество дисперсии перед размахом в том, что дисперсию можно представить как сумму ряда чисел (согласно ее определению), т. е. разложить на составные компоненты, позволяя тем самым более подробно охарактеризовать исходную выборку. Важная характеристика дисперсии заключается также и в том, что с её помощью можно сравнивать выборки, различные по объему. Однако сама дисперсия, как характеристика отклонения от среднего, часто неудобна для интерпретации. Так, например, предположим, что в эксперименте измерялся рост в сантиметрах, тогда размерность дисперсии будет являться характеристикой площади, а не линейного размера (поскольку при подсчете дисперсии сантиметр возводится в квадрат). Для того чтобы приблизить размерность дисперсии к размерности измеряемого признака применяют операцию извлечения квадратного корня из дисперсии. Полученную величину называют стандартным отклонением. Из суммы квадратов, деленных на число членов ряда извлекается квадратный корень.
Другими словами, стандартное отклонение выборки Sx представляет собой корень квадратный, извлеченный из дисперсии выборки Стандартное отклонение для генеральной совокупности обозначают также символом 4.6. Степень свободы Число степеней свободы это число свободно варьирующих единиц в составе выборки. Так, если вся выборка состоит из п элементов и характеризуется средней Пример. Рассмотрим ряд (4.5): Мы помним, что средняя этого ряда равна 6. В этом ряду 5 чисел, следовательно N = 5. Предположим, что мы хотим получить последний элемент ряда (4.5) — 10, зная все предыдущие элементы и среднее этого ряда. Тогда:
Предположим, что мы хотим получить первый элемент ряда (4.5) — 2, зная все последующие элементы и среднее этого ряда. Тогда:
Следовательно, один элемент выборки не имеет свободы вариации и всегда может быть выражен через другие элементы и среднее. Это означает, что число степеней свободы у выборочного ряда обозначаемое в таких случаях символом При наличии не одного, а нескольких ограничений свободы вариации, число степеней свободы, обозначаемое как В общем случае для таблицы экспериментальных данных число степеней свободы будет определяться по следующей формуле:
где с — число столбцов, а п — число строк (число испытуемых). Следует подчеркнуть, однако, что для ряда статистических методов расчет числа степеней свободы имеет свою специфику.
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 1711; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.198.21 (0.046 с.) |
 борке варьируют в пределах от минимального до максимального значения. Этот предел разбивают на так называемые классовые интервалы, которые, в зависимости от конкретных данных, могут быть как равными по величине, так и неравными.
борке варьируют в пределах от минимального до максимального значения. Этот предел разбивают на так называемые классовые интервалы, которые, в зависимости от конкретных данных, могут быть как равными по величине, так и неравными. .
.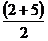 = 3,5
= 3,5 (X с волной или Md) и определяется как величина, по отношению к которой по крайней мере 50% выборочных значений меньше неё и по крайней мере 50% — больше. Можно дать второе определение, сказав, что медиана — это значение, которое делит упорядоченное множество данных пополам.
(X с волной или Md) и определяется как величина, по отношению к которой по крайней мере 50% выборочных значений меньше неё и по крайней мере 50% — больше. Можно дать второе определение, сказав, что медиана — это значение, которое делит упорядоченное множество данных пополам. 4.3. Среднее арифметическое
4.3. Среднее арифметическое числовых значений
числовых значений 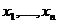 обозначается
обозначается  и подсчитывается как:
и подсчитывается как: (4.1)
(4.1) раз, среднюю арифметическую вычисляют по формуле:
раз, среднюю арифметическую вычисляют по формуле: .(4.2)
.(4.2) является символом операция суммирования. Он означает, что все значения
является символом операция суммирования. Он означает, что все значения 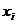 должны быть просуммированы. Числа, стоящие над и под знаком
должны быть просуммированы. Числа, стоящие над и под знаком  называются пределами суммирования и указывают наибольшее и наименьшее значения индекса суммирования, между которыми расположены его промежуточные значения.
называются пределами суммирования и указывают наибольшее и наименьшее значения индекса суммирования, между которыми расположены его промежуточные значения. = 1, и заканчивается последним, поэтому наверху символа суммирования
= 1, и заканчивается последним, поэтому наверху символа суммирования  то, поскольку нижний индекс суммирования
то, поскольку нижний индекс суммирования 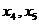 и
и  в результате будет получено:
в результате будет получено:  . Или, если будет написано следующее выражение:
. Или, если будет написано следующее выражение:  , то, поскольку нижний индекс суммирования
, то, поскольку нижний индекс суммирования 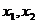 и
и  ряда, и в итоге будет получено:
ряда, и в итоге будет получено: 
 или
или  .
. (4.3)
(4.3)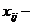 значения всех переменных, полученных в эксперименте, или все элементы таблицы;
значения всех переменных, полученных в эксперименте, или все элементы таблицы; меняется от 1 до р, где р число столбцов в таблице, а индекс
меняется от 1 до р, где р число столбцов в таблице, а индекс  очень удобно. Например, пусть перед нами стоит задача — указать конкретный элемент нашей таблицы. Для этого мы должны знать номер столбца, например 4, и номер строки (или порядковый номер испытуемого), например 5. Тогда его обозначение будет таково:
очень удобно. Например, пусть перед нами стоит задача — указать конкретный элемент нашей таблицы. Для этого мы должны знать номер столбца, например 4, и номер строки (или порядковый номер испытуемого), например 5. Тогда его обозначение будет таково:  . Это значит, что выбран пятый элемент в строчке из четвертого столбца.
. Это значит, что выбран пятый элемент в строчке из четвертого столбца. (двойная сумма) означает, что вначале осуществляется суммирование всех элементов таблицы по индексу
(двойная сумма) означает, что вначале осуществляется суммирование всех элементов таблицы по индексу 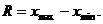
 =1032
=1032  = 30
= 30  = 40
= 40 , (4.4)
, (4.4) .
.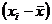 для каждого элемента ряда. Иными словами, из каждого элемента ряда 4.5 вычтем величину среднего этого ряда. Полученные величины характеризуют то, насколько каждый элемент отклоняется от средней величины в данном ряду. Обозначим полученную совокупность разностей как множество Т. Тогда Т есть:
для каждого элемента ряда. Иными словами, из каждого элемента ряда 4.5 вычтем величину среднего этого ряда. Полученные величины характеризуют то, насколько каждый элемент отклоняется от средней величины в данном ряду. Обозначим полученную совокупность разностей как множество Т. Тогда Т есть: == -4; 4 - 6 = -2; 6 - 6 = 0; 8 - 6 = 2;= 4).
== -4; 4 - 6 = -2; 6 - 6 = 0; 8 - 6 = 2;= 4).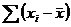 всегда будет равна нулю, т. е.
всегда будет равна нулю, т. е. 


 . (4.6)
. (4.6) — значения всех переменых, полученных в эксперименте, или все элементы таблицы;
— значения всех переменых, полученных в эксперименте, или все элементы таблицы; , а дисперсию выборки как
, а дисперсию выборки как  , причем индекс х обозначает, что дисперсия характеризует варьирование числовых значений признака вокруг их средней арифметической.
, причем индекс х обозначает, что дисперсия характеризует варьирование числовых значений признака вокруг их средней арифметической. (4.7)
(4.7)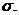 Подчеркнем еще раз, что размерность стандартного отклонения и размерность исходного ряда совпадают. В нашем примере
Подчеркнем еще раз, что размерность стандартного отклонения и размерность исходного ряда совпадают. В нашем примере  .
. и суммой всех остальных элементов, кроме самого этого элемента.
и суммой всех остальных элементов, кроме самого этого элемента. = 10.
= 10. будет определяться как
будет определяться как  (греческая буква ню) будет равно
(греческая буква ню) будет равно 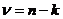 , где
, где  . (4.8)
. (4.8)


