
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проблема измерения индивидуальных психологических особенностей.Стр 1 из 9Следующая ⇒
Вопросы к зачету Проблема измерения индивидуальных психологических особенностей. Понятие измерения. Виды измерительных шкал и свойства психологических объектов измерения. Измерение – приписывание числовых форм объектам\событиям в соответствии с определенными правилами. Это правило устанавливает соответствие между измеряемым свойством объекта и результатом измерения признака. Виды измерений: 1 Нормативное – результат испытуемого сравнивается с результатом других людей (эталонной группой лиц) 2 Критериально е - результат испытуемого сравнивается с каким-то критерием; определяется не относительный, а абсолютный статус 3 Ипсативно е - результат испытуемого сравнивается с его предыдущим уровнем Проблема измерения в психологии связана с: -объектом измерения (человеком) - методами измерения (тест) - исследователем, испытателем, эксперементатором. Измерения в психологии — процедуры определения количественной выраженности психологических феноменов. В них применяются разнообразные шкалы, содержащие некое множество позиций, поставленных в некое соответствие с психологическими элементами. Шкалирование. Шкала измерения – форма фиксации результатов измерения с упорядочиванием их в определенную числовую систему. Классификация шкал измерения (С. Стивенс). А)неметрические измерительные шкалы Номинативная шкала (неметрическая), или шкала наименований - это шкала, классифицирующая по названию (лат. nomen - имя, название). В её основе лежит процедура, обычно не ассоциируемая с измерением. Пользуясь определённым правилом, объекты группируются по различным классам так, чтобы внутри класса они были идентичны по измеряемому свойству. Затем каждому объекту присваивается соответствующее обозначение. Простейший случай номинативной шкалы - дихотомическая шкала, состоящая всего лишь из двух ячеек, например: «имеет братьев и сестер - единственный ребенок в семье»; «иностранец – соотечественник»; проголосовал «за» - проголосовал «против» и т.п. Признак, который измеряется по дихотомической шкале наименований, называется альтернативным. Он может принимать всего два значения. При этом исследователь зачастую заинтересован в одном из них, и тогда он говорит, что признак «проявился», если тот принял интересующее его значение, и что признак «не проявился», если он принял противоположное значение. Например: «Признак леворукости проявился у 8 испытуемых из 20». В принципе номинативная шкала может состоять из ячеек «признак проявился - признак не проявился».
Примером шкалы такого рода может служить классификация испытуемых на мужчин и женщин Порядковая шкала, или ранговая шкала - это шкала, классифицирующая по принципу «больше – меньше» (в соответствии с возрастанием или убыванием значений общего для этих объектов признака). Как следует из названия, измерение в этой шкале предполагает приписывание объектам чисел в зависимости от степени выраженности измеряемого свойства. Если в шкале наименований было безразлично, в каком порядке мы расположим классификационные ячейки, то в порядковой шкале они образуют последовательность от ячейки «самое малое значение» к ячейке «самое большое значение» (или наоборот). Ячейки теперь уместнее называть классами, поскольку по отношению к классам употребимы определения «низкий», «средний» и «высокий» класс (ранг), или 1-й, 2-й, 3-й класс, и т.д. Каждому объекту приписывается число, которое называется ранг, а процесс измерения по этой шкале – ранжирование. В порядковой шкале должно быть не менее трех классов например «положительная реакция - нейтральная реакция - отрицательная реакция» или «подходит для занятия вакантной должности - подходит с оговорками - не подходит» и т. п. Пример метод экспертных оценок. К примеру, когда человека просят проранжировать цвета по предпочтению, от самого приятного, до самого неприятного. В этом случае, мы точно можем сказать, что один цвет приятнее другого, но о единицах измерения мы не можем даже предположить, т.к. человек ранжировал цвета не на основе каких-либо единиц измерения, а основываясь на собственных чувствах. То же самое происходит в тесте Рокича, по результатам которого мы так же не знаем на сколько единиц одна ценность выше (больше) другой. Т.е., в отличие от соревнований, мы даже не имеем возможности узнать точные баллы различий.
Б)метрические измерительные шкалы. Интервальная шкала – произвольно выбирается нулевая точка (не значит, что свойство полностью отсутствует) и единица измерения; это шкала, классифицирующая по принципу «больше на определенное количество единиц - меньше на определенное количество единиц». Каждое из возможных значений признака отстоит от другого на равном расстоянии. Шкала интервалов определяет величину различий между объектами в проявлении свойства. Она дополняет идею ранжирования принципом равных интервалов между ранжируемыми явлениями. * Если объектам А и Б приписаны разные интервальные оценки, то можно сказать насколько эти объекты отличаются. Наиболее распространенный пример использования интервальной шкалы — психологические тесты личности, установок и способностей. Например, результаты теста интеллекта обычно представляются подобным образом. Некто, имеющий IQ 120, предполагается более умным (предположим, что IQ определяет умственные способности), чем тот, чей IQ равен 110. Шкала равных отношений или абсолютная шкала – характеризуется тем, что нулевая точка зафиксирована и обозначает полное отсутствие признака; это шкала, классифицирующая объекты или субъектов пропорционально степени выраженности измеряемого свойства. По отношению к показателям частот возможно применять все арифметические операции: сложение, вычитание, деление и умножение. Единица измерения в этой шкале отношений - 1 наблюдение, 1 выбор, 1 реакция и т. п. Мы вернулись к тому, с чего начали: к универсальной шкале измерения в частотах встречаемости того или иного значения признака и к единице измерения, которая представляет собой 1 наблюдение. * Если объектам А и Б разные показатели, то можно сказать насколько и во сколько раз они отличаются. Пример любые признаки, значения которых получается при счете (количество выборов, ошибок) 1. Дихотомическая классификация часто рассматривается как вариант шкалы наименований. Это верно, за исключением одного случая, когда мы измеряем свойство, имеющее всего лишь два уровня выраженности: «есть—нет», так называемое «точечное» свойство. Примеров таких свойств много: наличие или отсутствие у испытуемого какой-либо наследственной болезни (дальтонизм, болезнь Дауна, гемофилия и др.), абсолютного слуха и др. В этом случае исследователь имеет право проводить «оцифровку» данных, присваивая каждому из типов цифру «1» или «0», и работать с ними как со значениями шкалы интервалов.
Признаки и переменные. Признаки и переменные - это измеряемые психологические явления. Такими явлениями могут быть время решения задачи, количество допущенных ошибок, уровень тревожности, показатель интеллектуальной лабильности, интенсивность агрессивных реакций, угол поворота корпуса в беседе, показатель социометрического статуса и множество других переменных. Понятия признака и переменной могут использоваться как взаимозаменяемые. Они являются наиболее общими. Иногда вместо них используются понятия показателя или уровня, например, уровень настойчивости, показатель вербального интеллекта и др. Понятия показателя и уровня указывают на то, что признак может быть измерен количественно, так как к ним применимы определения высокий или низкий, например, высокий уровень интеллекта, низкие показатели тревожности и др.
Психологические переменные являются случайными величинами, поскольку заранее неизвестно, какое именно значение они примут. Математическая обработка - это оперирование со значениями признака, полученными у испытуемых в психологическом исследовании. Такие индивидуальные результаты называют также: наблюдениями, наблюдаемыми значениями, вариантами, датами, индивидуальными показателями и др. В психологии чаще всего используются термины наблюдение или наблюдаемое значение.
Понятие выборки и ее объем. Зависимые и независимые выборки. Требования к выборке при решении различных задач. Полное исследование Если психологическому исследованию (наблюдению, измерению, эксперименту) подвергаются все представители изучаемой генеральной совокупности, то такое исследование называют полным, или сплошным. Предполагается, что, в соответствии с задачами, гипотезами и планом, полное обследование генеральной совокупности позволяет получить исчерпывающую информацию об изучаемых в ней психологических закономерностях. Однако в отечественной и зарубежной психологии еще никогда не проводилось сплошного исследования по той причине, что на практике определить размеры той или иной генеральной совокупности и тем более исследовать её — задача нереальная и, кроме того, в определенной степени избыточная. Если выборка испытуемых по своим характеристикам репрезентативна генеральной совокупности, то есть основания полученные при её изучении результаты распространить на всю генеральную совокупность. Нельзя упускать из вида также и то, что работа психолога, по существу, представляет собой сложный вид деятельности, требующий высокой профессиональной компетентности и нередко много времени для работы с каждым испытуемым. Выборочное исследование Если психолог производит выбор ограниченного числа элементов из изучаемой (генеральной) совокупности, то такое исследование называют частичным, или выборочным. Выборочный метод является основным в экспериментальной работе психолога при изучении генеральных совокупностей. Его преимущество перед полным (сплошным) исследованием всех элементов генеральной совокупности заключается в том, что он сокращает как время, так и затраты труда, а главное — позволяет получать информацию о таких группах, полное обследование которых принципиально невозможно или нецелесообразно.
Требования к выборке К выборке применяется ряд обязательных требований, определенных прежде всего целями и задачами исследования. Планирование эксперимента должно включать в себя учет как объема выборки, так и ряда ее особенностей. Так, в психологических исследованиях важно требование однородности выборки. Оно означает, что психолог, изучая, например, подростков, не может, включать в эту же выборку взрослых людей. Напротив, исследование, выполненное методом возрастных срезов, принципиально предполагает наличие разновозрастных испытуемых. Однако и в этом случае должна соблюдаться однородность выборки, но уже по другим критериям, в первую очередь таким, как возраст, пол. Основаниями для формирования однородной выборки могут служить разные характеристики, такие, как уровень интеллекта, национальность, отсутствие определенных заболеваний и т.д., в зависимости от целей исследования. В общей статистике имеется понятие повторной и бесповторной выборки, или, иначе говоря, выборки с возвратом и без возврата. В качестве примера приводится, как правило, выбор шара, доставаемого из какой-либо емкости. В случае выборки с возвратом каждый выбранный шар опять возвращается в емкость и, следовательно, может быть выбран снова. При бесповторном выборе однажды выбранный шар откладывается в сторону и больше не может участвовать в выборке. В психологических ис следованиях можно найти аналоги подобного рода способам организации выборочного исследования, поскольку психологу нередко приходится несколько раз тестировать одних и тех же испытуемых при помощи одной и той же методики. Однако, строго говоря, повторной в этом случае является процедура тестирования. Выборка испытуемых при полной тождественности состава в случае повторных исследований всегда будет иметь некоторые отличия, обусловленные функциональной и возрастной изменчивостью, присущей всем людям. Подобная выборка по характеру проведения процедуры является повторной, хотя смысл термина здесь, очевидно, иной, чем в случае с шарами. Важно подчеркнуть, что все требования, предъявляемые к любой выборке, сводятся к тому, что на ее основе психологом должна быть получена наиболее полная, неискаженная информация об особенностях генеральной совокупности, из которой взята эта выборка. Иными словами, выборка должна как можно более полно отражать характеристики изучаемой генеральной совокупности. Репрезентативность выборки Cостав экспериментальной выборки должен представлять (моделировать) генеральную совокупность, поскольку выводы, полученные в эксперименте, предполагается в дальнейшем перенести на всю генеральную совокупность. Поэтому выборка должна обладать особым качеством — репрезентативность, позволяющим распространить полученные на ней выводы на всю генеральную совокупность.
Репрезентативность выборки очень важна, тем не менее по объективным причинам соблюдать её крайне сложно. Так, хорошо известен факт, что от 70% до 90% всех психологических исследований поведения человека проводились в США в 60-х годах XX века с испытуемыми-студентами колледжей, причем большинство из них были студентами психологами. В лабораторных исследованиях, выполняемых на животных, наиболее распространенным объектом изучения являются крысы. Поэтому неслучайно психологию называли раньше «наукой о студентах-второкурсниках и белых крысах». Студенты психологических колледжей составляют всего 3% от общей численности населения США. Очевидно, что выборка студентов нерепрезентативна в качестве модели, претендующей на представительство всего населения страны. Репрезентативная выборка, или, как еще говорят, представительная выборка, — это такая выборка, в которой все основные признаки генеральной совокупности представлены приблизительно в той же пропорции и с той же частотой, с которой данный признак выступает в данной генеральной совокупности. Иными словами, репрезентативная выборка представляет собой меньшую по размеру, но точную модель той генеральной совокупности, которую она должна отражать. В той степени, в какой выборка является репрезентативной, выводы, основанные на изучении этой выборки, можно с большой долей уверенности считать применимыми ко всей генеральной совокупности. Это распространение результатов называется генерализуемостью. В идеале репрезентативная выборка должна быть такой, чтобы каждая из основных изучаемых психологом характеристик, черт, особенностей личности и т.п. была бы представлена в ней пропорционально этим же особенностям в генеральной совокупности. Согласно этим требованиям процедура формирования выборки должна иметь внутреннюю логику, способную убедить исследователя, что при сравнении с генеральной совокупностью она действительно окажется репрезентативной, представительной. В своей конкретной деятельности психолог действует следующим образом: устанавливает подгруппу (выборку) внутри генеральной совокупности, подробно изучает эту выборку (проводит с ней экспериментальную работу), а затем, если это позволяют результаты статистического анализа, распространяет полученные выводы на всю генеральную совокупность. Это и есть основные этапы работы психолога с выборкой. Начинающий психолог должен иметь в виду часто повторяющуюся ошибку: каждый раз, когда он осуществляет сбор любых данных любым методом и из любого источника, у него всегда появляется соблазн распространить свои выводы на всю генеральную совокупность. Для того чтобы избежать подобной ошибки, надо не просто обладать здравым смыслом, но, прежде всего, хорошо владеть основными понятиями математической статистики. Рекомендации к выбору критериев. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ Для экспериментальных данных, полученных по выборке, можно вычислить ряд числовых характеристик (мер). Мода Числовой характеристикой выборки, как правило, не требующей вычислений, является так называемая мода. Мода — это такое числовое значение, которое встречается в выборке наиболее часто. Мода обозначается иногда как Так, например, в ряду значений (2, 6, 6, 8, 9, 9, 9, 10) модой является 9, потому что 9 встречается чаще любого другого числа. Обратите внимание, что мода представляет собой наиболее часто встречающееся значение (в данном примере это 9), а не частоту встречаемости этого значения (в данном примере равную 3). Моду находят согласно следующим правилам: 1) В том случае, когда все значения в выборке встречаются одинаково часто, принято считать, что этот выборочный ряд не имеет моды. Например: 5, 5, 6, 6, 7, 7 — в этой выборке моды нет. 2) Когда два соседних (смежных) значения имеют одинаковую частоту и их частота больше частот любых других значений, мода вычисляется как среднее арифметическое этих двух значений. Например, в выборке 1, 2, 2, 2, 5, 5, 5, 6 частоты рядом расположенных значений 2 и 5 совпадают и равняются 3. Эта частота больше, чем частота других значений 1 и 6 (у которых она равна 1). Следовательно, модой этого ряда будет величина 3) Если два несмежных (не соседних) значения в выборке имеют равные частоты, которые больше частот любого другого значения, то выделяют две моды. Например, в ряду 10, 11, 11, 11, 12, 13, 14, 14, 14, 17 модами являются значения 11 и 14. В таком случае говорят, что выборка является бимодальной. Могут существовать и так называемые мультимодальные распределения, имеющие более двух вершин (мод). 3) Если мода оценивается по множеству сгруппированных данных, то для нахождения моды необходимо определить группу с наибольшей частотой признака. Эта группа называется модальной группой. Медиана Медиана — обозначается Задача 4.1. Найдем медиану выборки: 9, 3, 5, 8, 4, 11, 13. Решение. Сначала упорядочим выборку по величинам входящих в нее значений. Получим: 3, 4, 5, 8, 9, 11, 13. Поскольку в выборке семь элементов, четвертый по порядку элемент будет иметь значение большее, чем первые три, и меньшее, чем последние три. Таким образом, медианой будет четвертый элемент — 8. Задача 4.2. Найдем медиану выборки: 20, 9, 13, 1, 4, 11. Упорядочим выборку: 1, 4, 9, 11, 13, 20. Поскольку здесь имеется четное число элементов, то существует две «середины» — 9 и 11. В этом случае медиана определяется как среднее арифметическое этих значений.
Среднее арифметическое ряда из
Здесь величины 1, 2...п являются так называемыми индексами. В том случае, если отдельные значения выборки повторяются
в таком случае называют взвешенной средней, где Знак Например, в формуле (4.1) суммирование начинается с первого элемента выборки, поэтому и пишется так: Если же мы запишем так: В дальнейшем мы будем пользоваться сокращением, которое состоит в том, что если производится суммирование всех элементов выборки от первого до последнего, то верхний и нижний пределы суммирования указываться не будут, а пишется просто:
При вычислении величины средней по таблице чисел в дальнейшем будет использоваться следующая формула:
где при этом индекс Тогда Символическое обозначение Символ Следует подчеркнуть, что средние величины характеризуют выборку одним (средним) числом. Преимущество, или иначе, информативная значимость, средних величин заключается в их способности аккумулировать или уравновешивать все индивидуальные отклонения, в результате чего проявляется то наиболее устойчивое и типичное, что характеризует качественное своеобразие варьирующего объекта, позволяя отличить одну выборку от другой, а на этой основе, например, одно измеренное психологическоесвойство от другого. Однако среднее как статистический показатель не лишено недостатков. Так, например, при вычислении среднего количества ошибок при выполнении корректурной пробы может быть получена величина равная 1,3 ошибки или при определении среднего числа учеников, обучающихся в пятых классах данной школы, может быть получена величина равная 30,07. Конечно, с точки зрения статистика эти величины обычны, но для психологических задач они могут быть неприемлемы. Кроме того, среднее оказывается достаточно чувствительным к очень маленьким или очень большим величинам, отличающимся от основных значений измеренных характеристик. Приведем пример из книги Дж. Б. Мангейма и Ричарда К. Рича: «Политология. Методы исследования» М., 1997 г. «Пусть 9 человек имеют доход от 4500 до 5200 тыс. долларов в месяц. Величина их среднего дохода равняется 4900 долларов. Если же к этой группе добавить человека, имеющего доход в 20000 тыс. долларов в месяц, то средняя всей группы сместится и окажется равной 6410 Долларов, хотя никто из всей выборки (кроме одного человека) реально не получает такой суммы. Понятно, что аналогичное смещение, но в противоположную сторону можно получить и в том случае, если добавить в эту группу человека с очень маленьким годовым доходом». Важно подчеркнуть, что подобные крайние величины, т. е. те, которые существенно искажают величину средней, оказываются в то же время и наименее характерными для изучаемой генеральной совокупности. Именно поэтому в статистике, кроме средней величины, используются и другие характеристики «типичных значений» выборки, такие, как мода, медиана и ряд других характеристик. 4.4. Разброс выборки Разброс (иногда эту величину называют размахом) выборки обозначается буквой R. Это самый простой показатель, который можно получить для выборки — разность между максимальной и минимальной величинами данного конкретного вариационного ряда, т. е.
Понятно, что чем сильнее варьирует измеряемый признак, тем больше величина R, и наоборот. Однако может случиться так, что у двух выборочных рядов и средние, и размах совпадают, однако характер варьирования этих рядов будет различный. Например, даны две выборки: X = 1040
При равенстве средних и разбросов для этих двух выборочных рядов характер их варьирования различен. Для того чтобы более четко представлять характер варьирования выборок, следует обратиться к их распределениям. 4.5. Дисперсия Рассмотрим еще одну очень важную числовую характеристику выборки, называемую дисперсией. Дисперсия представляет собой наиболее часто использующуюся меру рассеяния случайной величины (переменной). Дисперсия это среднее арифметическое квадратов отклонений значений переменной от её среднего значения.
где п — объем выборки — индекс суммирования
Вычислим дисперсию следующего ряда Прежде всего найдем среднее ряда (4.5). Оно равно Рассмотрим величины:
Так образуется новый ряд чисел. Его особенность в том, что Получить полный текст Отметим, что сумма такого ряда Для того чтобы избавиться от нуля, каждое значение разности
Это и есть искомая дисперсия. Общий алгоритм вычисления дисперсии для одной выборки следующий: 1. Вычисляется среднее по выборке. 2. Для каждого элемента выборки вычисляется его отклонение от средней, т. е. получается множество Т. 3. Каждый элемент множества Т возводят в квадрат. 4. Находится сумма этих квадратов. 5. Эта сумма, как и в случае вычисления среднего, делится на общее количество членов ряда — п. В ряде случаев, особенно когда величина выборки мала, деление осуществляется не на величину п, а на величину п —1. Величина, получающаяся после пятого шага, и есть искомая дисперсия. Расчет дисперсии для таблицы чисел осуществляется по формуле 4.6:
где индекс j меняется от 1 до р, где р число столбцов в таблице, а индекс
N — общее число всех элементов в таблице (анализируемой совокупности экспериментальных данных) и в общем случае N = Дисперсию для генеральной совокупности принято обозначать как Преимущество дисперсии перед размахом в том, что дисперсию можно представить как сумму ряда чисел (согласно ее определению), т. е. разложить на составные компоненты, позволяя тем самым более подробно охарактеризовать исходную выборку. Важная характеристика дисперсии заключается также и в том, что с её помощью можно сравнивать выборки, различные по объему. Однако сама дисперсия, как характеристика отклонения от среднего, часто неудобна для интерпретации. Так, например, предположим, что в эксперименте измерялся рост в сантиметрах, тогда размерность дисперсии будет являться характеристикой площади, а не линейного размера (поскольку при подсчете дисперсии сантиметр возводится в квадрат). Для того чтобы приблизить размерность дисперсии к размерности измеряемого признака применяют операцию извлечения квадратного корня из дисперсии. Полученную величину называют стандартным отклонением. Из суммы квадратов, деленных на число членов ряда извлекается квадратный корень.
Другими словами, стандартное отклонение выборки Sx представляет собой корень квадратный, извлеченный из дисперсии выборки Стандартное отклонение для генеральной совокупности обозначают также символом 4.6. Степень свободы Число степеней свободы это число свободно варьирующих единиц в составе выборки. Так, если вся выборка состоит из п элементов и характеризуется средней Пример. Рассмотрим ряд (4.5): Мы помним, что средняя этого ряда равна 6. В этом ряду 5 чисел, следовательно N = 5. Предположим, что мы хотим получить последний элемент ряда (4.5) — 10, зная все предыдущие элементы и среднее этого ряда. Тогда:
Предположим, что мы хотим получить первый элемент ряда (4.5) — 2, зная все последующие элементы и среднее этого ряда. Тогда:
Следовательно, один элемент выборки не имеет свободы вариации и всегда может быть выражен через другие элементы и среднее. Это означает, что число степеней свободы у выборочного ряда обозначаемое в таких случаях символом При наличии не одного, а нескольких ограничений свободы вариации, число степеней свободы, обозначаемое как В общем случае для таблицы экспериментальных данных число степеней свободы будет определяться по следующей формуле:
где с — число столбцов, а п — число строк (число испытуемых). Следует подчеркнуть, однако, что для ряда статистических методов расчет числа степеней свободы имеет свою специфику. Таблица исходных данных Обычно в ходе исследования интересующий исследователя признак измеряется не у одного - двух, а у множества объектов (испытуемых). Кроме того, каждый объект характеризуется не одним, а целым рядом признаков, измеренных в разных шкалах. Одни признаки представлены в номинативной шкале и указывают на принадлежность испытуемых к той или иной группе (пол, профессия, контрольная или экспериментальная группа и т. д.). Другие признаки могут быть представлены в порядковой или метрической шкале. Поэтому результаты измерения для дальнейшего анализа чаще всего представляют в виде таблицы исходных данных. Каждая строка такой таблицы обычно соответствует одному объекту, а каждый столбец - одному измеренному признаку. Таким образом, исходной формой представления данных является таблица типа «объект - признак». В ходе дальнейшего анализа каждый признак выступает в качестве переменной величины, или просто - переменной, значения которой меняются от объекта к объекту. Пример _____________
|
|||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 743; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.33.41 (0.141 с.) |
 .
.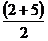 = 3,5
= 3,5 (X с волной или Md) и определяется как величина, по отношению к которой по крайней мере 50% выборочных значений меньше неё и по крайней мере 50% — больше. Можно дать второе определение, сказав, что медиана — это значение, которое делит упорядоченное множество данных пополам.
(X с волной или Md) и определяется как величина, по отношению к которой по крайней мере 50% выборочных значений меньше неё и по крайней мере 50% — больше. Можно дать второе определение, сказав, что медиана — это значение, которое делит упорядоченное множество данных пополам. 4.3. Среднее арифметическое
4.3. Среднее арифметическое числовых значений
числовых значений 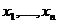 обозначается
обозначается  и подсчитывается как:
и подсчитывается как: (4.1)
(4.1) раз, среднюю арифметическую вычисляют по формуле:
раз, среднюю арифметическую вычисляют по формуле: .(4.2)
.(4.2) является символом операция суммирования. Он означает, что все значения
является символом операция суммирования. Он означает, что все значения 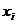 должны быть просуммированы. Числа, стоящие над и под знаком
должны быть просуммированы. Числа, стоящие над и под знаком  называются пределами суммирования и указывают наибольшее и наименьшее значения индекса суммирования, между которыми расположены его промежуточные значения.
называются пределами суммирования и указывают наибольшее и наименьшее значения индекса суммирования, между которыми расположены его промежуточные значения. = 1, и заканчивается последним, поэтому наверху символа суммирования
= 1, и заканчивается последним, поэтому наверху символа суммирования  то, поскольку нижний индекс суммирования
то, поскольку нижний индекс суммирования 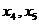 и
и  в результате будет получено:
в результате будет получено:  . Или, если будет написано следующее выражение:
. Или, если будет написано следующее выражение:  , то, поскольку нижний индекс суммирования
, то, поскольку нижний индекс суммирования 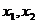 и
и  ряда, и в итоге будет получено:
ряда, и в итоге будет получено: 
 или
или  .
. (4.3)
(4.3)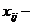 значения всех переменных, полученных в эксперименте, или все элементы таблицы;
значения всех переменных, полученных в эксперименте, или все элементы таблицы; меняется от 1 до р, где р число столбцов в таблице, а индекс
меняется от 1 до р, где р число столбцов в таблице, а индекс  очень удобно. Например, пусть перед нами стоит задача — указать конкретный элемент нашей таблицы. Для этого мы должны знать номер столбца, например 4, и номер строки (или порядковый номер испытуемого), например 5. Тогда его обозначение будет таково:
очень удобно. Например, пусть перед нами стоит задача — указать конкретный элемент нашей таблицы. Для этого мы должны знать номер столбца, например 4, и номер строки (или порядковый номер испытуемого), например 5. Тогда его обозначение будет таково:  . Это значит, что выбран пятый элемент в строчке из четвертого столбца.
. Это значит, что выбран пятый элемент в строчке из четвертого столбца. (двойная сумма) означает, что вначале осуществляется суммирование всех элементов таблицы по индексу
(двойная сумма) означает, что вначале осуществляется суммирование всех элементов таблицы по индексу 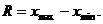
 =1032
=1032  = 30
= 30  = 40
= 40 , (4.4)
, (4.4) .
.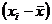 для каждого элемента ряда. Иными словами, из каждого элемента ряда 4.5 вычтем величину среднего этого ряда. Полученные величины характеризуют то, насколько каждый элемент отклоняется от средней величины в данном ряду. Обозначим полученную совокупность разностей как множество Т. Тогда Т есть:
для каждого элемента ряда. Иными словами, из каждого элемента ряда 4.5 вычтем величину среднего этого ряда. Полученные величины характеризуют то, насколько каждый элемент отклоняется от средней величины в данном ряду. Обозначим полученную совокупность разностей как множество Т. Тогда Т есть: == -4; 4 - 6 = -2; 6 - 6 = 0; 8 - 6 = 2;= 4).
== -4; 4 - 6 = -2; 6 - 6 = 0; 8 - 6 = 2;= 4).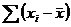 всегда будет равна нулю, т. е.
всегда будет равна нулю, т. е. 


 . (4.6)
. (4.6) — значения всех переменых, полученных в эксперименте, или все элементы таблицы;
— значения всех переменых, полученных в эксперименте, или все элементы таблицы; , а дисперсию выборки как
, а дисперсию выборки как  , причем индекс х обозначает, что дисперсия характеризует варьирование числовых значений признака вокруг их средней арифметической.
, причем индекс х обозначает, что дисперсия характеризует варьирование числовых значений признака вокруг их средней арифметической. (4.7)
(4.7)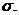 Подчеркнем еще раз, что размерность стандартного отклонения и размерность исходного ряда совпадают. В нашем примере
Подчеркнем еще раз, что размерность стандартного отклонения и размерность исходного ряда совпадают. В нашем примере  .
. и суммой всех остальных элементов, кроме самого этого элемента.
и суммой всех остальных элементов, кроме самого этого элемента. = 10.
= 10. будет определяться как
будет определяться как  (греческая буква ню) будет равно
(греческая буква ню) будет равно 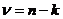 , где
, где  . (4.8)
. (4.8)


