
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 1. 4 использование программы Excel в линейной алгебреСодержание книги Поиск на нашем сайте
Цель занятия: Научиться производить о перации с матрицами в Excel.
Матрицей размера m*n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы и обозначаются строчными буквами с двойной индексацией:
Операции с матрицами. Транспонирование Транспонированной (обратной) называется матрица, в которой столбцы исходной матрицы заменяются строками с соответствующими номерами. Исходная матрица: А = (аij), транспонированная – Ат = (аji).
Для осуществления транспонирования в Excel используется функция ТРАНСП в категории Ссылки и массивы, которая позволяет менять ориентацию массива. Функция имеет вид ТРАНСП(массив). Массив – это диапазон ячеек на рабочем листе, в котором записаны элементы матрицы. Пример 1. Дана матрица А, получить транспонированную матрицу Ат.
Решение. 1. Введите на рабочий лист Excel предложенную матрицу (в ячейку число). Выделите указателем мыши блок ячеек под транспонированную матрицу (размер транспонированной матрицы: количество строк = количеству столбцов в исходной матрице). В данном случае размер исходной матрицы 2*5, транспонированной – 5*2. 2. Меню Вставка – Функция, в появившемся диалоговом окне Мастер функций в рабочем поле Категория выберите Ссылки и массивы, в рабочем поле функции – имя функции ТРАНСП. 3. В окне ТРАНСП укажите диапазон ячеек исходной матрицы. После чего нажмите сочетание клавиш CTRL+SHIFT+ENTER. 4. В указанном вами диапазоне должна появиться транспонированная матрица. Вычисление определителя матрицы. Важной характеристикой квадратных матриц является их определитель. Определитель матрицы – это число, вычисляемое на основе значений элементов массива. Определить матрицы обозначается как В Excel для вычисления определителя матрицы используют функцию МОПРЕД в категории Математические. Функция имеет вид МОПРЕД (массив). Здесь массив – это числовой массив, в котором хранится матрица с равным количеством строк и столбцов. Пример 2. Найти определитель матрицы
Решение.
Умножение матриц. Произведение матриц определено, если число столбцов первой матрицы равно числу строк второй. Для нахождения произведения двух матриц в Excel используется функция МУМНОЖ, которая вычисляет произведение матриц (матрицы хранятся в массивах). Функция имеет вид МУМНОЖ(массив1; массив 2). Здесь массив 1 и массив 2 – это перемножаемые матрицы. При этом количество столбцов аргумента массив 1 должно быть таким же, как количество строк аргумента массив 2, оба массива должны содержать только числа. Результатом (т.е. матрицей-произведением) является массив с таким же числом строк, как массив 1, и таким же числом столбцов, как массив 2. Пример 3. Найти произведение массивов Решение: 1. Введите матрицу А в диапазон А1:D3, а матрицу В в диапазон А4:В7. 2. Выделите блок ячеек под результирующую матрицу. Для этого необходимо найти размер матрицы-произведения. Ее размерность будет в данном примере 3*2. Выделите блок ячеек F1:G3. 3. Вызовите Мастер функций. В поле Категория выберите Математические, в поле Функции – имя функции МУМНОЖ. Нажмите ОК. В появившемся диалоговом окне введите диапазоны массива 1 и массива 2 (соответственно А1:D3 и А4:В7). После этого нажмите сочетание клавиш CTRL+SHIFT+ENTER. 4. После этого в выделенном вами диапазоне должна появится матрица, которая равна произведению исходных матриц. Упражнения. 1. Найдите матрицу, обратную данной и определитель исходной матрицы. 2. Найдите матрицу, обратную данной и определитель исходной матрицы 3. Найти произведение матриц А*В, где 4. Вычислите А*В =
|
|||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 184; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.155.254 (0.009 с.) |

 , где i – номер строки, j – номер столбца. Например,
, где i – номер строки, j – номер столбца. Например,


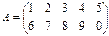
 или D. Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле
или D. Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле  .
.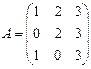
 и
и 








