
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методические указания для выполнения лабораторных работ по темеСодержание книги
Поиск на нашем сайте
Методические указания для выполнения лабораторных работ по теме Математика в «Excel» Оглавление Раздел 1. Аналитическая геометрия и линейная алгебра. 1 Тема 1.1 Декартова система координат. 1 Тема 1.2 Кривые второго порядка на плоскости. 2 Тема 1.3 Графическое решение системы уравнений. 2 Тема 1.4 Использование программы Excel в линейной алгебре. 3 Раздел 2. Элементы математического анализа. 4 Тема 2.1. Определенный интеграл. 5 Раздел 3. Задачи оптимизации. 6 Тема 3.1 Решение уравнения с одним неизвестным.. 6 Тема 3.2 Аппроксимация экспериментальных данных. 7
Раздел 1. Аналитическая геометрия и линейная алгебра Тема 1.1 Декартова система координат Самая простая и наиболее распространенная система координат на плоскости называется декартовой по имени известного математика и философа Рене Декарта. Декартова система координат образована двумя перпендикулярными осями, осью Х и осью Y. Точка пересечения осей называется началом и служит одновременно началом координат на каждой из осей. Масштаб на осях выбирается одинаковый (иначе система координат будет называться аффинной, а не декартовой). Прямая линия на плоскости Уравнением линии на плоскости x0y может записываться по разному:
Всегда важно указать, какие значения может принимать независимая переменная х. Собственно говоря, символом х обозначается произвольный элемент некоторого числового множества, которое называется областью определения функции. С помощью системы координат мы можем каждую функцию изобразить наглядно, в виде графика. В программе Excel для построения прямых, а также кривых, может быть использован специальный инструмент – Мастер диаграмм, который дает возможность строить различные типы графиков. Для применения Мастера диаграмм необходимо ввести точки прямой линии в рабочую таблицу, вызвать Мастер диаграмм, задать тип диаграммы, диапазоны данных и подписей оси x, ввести название осей. Пример.
Рассмотрим построение прямой в Excel на примере уравнения y=2x+1 на интервале Для решения задачи на чистый лист Excel занести значения аргумента и подсчитать значение функции. В ячейку A1 введите слово Аргумент, в ячейку B1 – слово Прямая. В ячейку А2 введите левую границу диапазона «-3». В ячейку А3 – «-2,5». Выделите блок ячеек А2:А3 и при помощи маркера заполнения протяните и заполните весь диапазон изменения аргумента. В ячейку В2 введите формулу =2*А2 + 1 (ссылку на ячейку можно заполнить при помощи щелчка на соответствующей ячейке). Затем с использованием маркера заполнения копируем эту формулу в весь диапазон. На Панели инструментов Стандартная необходимо нажать кнопку Мастер диаграмм. В появившемся диалоговом окне указать в правом поле тип диаграммы График и подтип диаграммы в правом поле – График с маркерами. После чего нажимаем в диалоговом окне кнопку Далее. В появившемся диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать вкладку Диапазон данных и в поле Диапазон указать интервал данных, т.е. ввести ссылку на ячейки, содержащие данные, необходимые для представления на диаграмме (при помощи мышки выделить диапазон В1:В14. В рабочем поле должна появиться надпись Лист1!$B$1:$B$14. Ряды в столбцах. Если диалоговое окно закрывает столбцы с данными, его можно отодвинуть, потянув за строку заголовка указателем мыши. Во вкладке Ряд этого же диалогового окна необходимо указать Подписи по оси Х. Для этого, поставив курсор в поле мышкой отметьте диапазон аргумента (Лист1!$A$2:$A$14). Нажмите кнопку Далее. В третьем окне Мастера диаграмм (шаг 3 из 4): параметры диаграммы нужно ввести заголовок диаграммы (если его нет) и название осей (во вкладке Заголовки). Во вкладке Легенда щелчком мыши установить флажок в поле добавить легенду. После чего нажать Далее. В четвертом окне Мастер диаграмм (шаг 4 из 4): размещение диаграммы необходимо указать место расположения диаграммы (на отдельном или текущем листе). Если диаграмма в демонстрационном поле имеет нужный вид, нажать кнопку Готово. В противном случае нажать кнопку Назад и изменить установки.
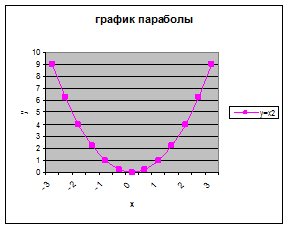
Пример. Построить параболу y=x2 в диапазоне хÎ[-3;3] с шагом 0,5. Решение.
Пусть открыть чистый рабочий лист, иначе добавить рабочий лист. По аналогии с предыдущим примером заполните исходные данные. Вызовите Мастер диаграмм. Постройте график функции y=x2.
Упражнения.
Операции с матрицами. Транспонирование Транспонированной (обратной) называется матрица, в которой столбцы исходной матрицы заменяются строками с соответствующими номерами. Исходная матрица: А = (аij), транспонированная – Ат = (аji).
Для осуществления транспонирования в Excel используется функция ТРАНСП в категории Ссылки и массивы, которая позволяет менять ориентацию массива. Функция имеет вид ТРАНСП(массив). Массив – это диапазон ячеек на рабочем листе, в котором записаны элементы матрицы. Пример 1. Дана матрица А, получить транспонированную матрицу Ат.
Решение. 1. Введите на рабочий лист Excel предложенную матрицу (в ячейку число). Выделите указателем мыши блок ячеек под транспонированную матрицу (размер транспонированной матрицы: количество строк = количеству столбцов в исходной матрице). В данном случае размер исходной матрицы 2*5, транспонированной – 5*2. 2. Меню Вставка – Функция, в появившемся диалоговом окне Мастер функций в рабочем поле Категория выберите Ссылки и массивы, в рабочем поле функции – имя функции ТРАНСП. 3. В окне ТРАНСП укажите диапазон ячеек исходной матрицы. После чего нажмите сочетание клавиш CTRL+SHIFT+ENTER. 4. В указанном вами диапазоне должна появиться транспонированная матрица. Пример 2. Найти определитель матрицы Решение.
Умножение матриц. Произведение матриц определено, если число столбцов первой матрицы равно числу строк второй. Для нахождения произведения двух матриц в Excel используется функция МУМНОЖ, которая вычисляет произведение матриц (матрицы хранятся в массивах). Функция имеет вид МУМНОЖ(массив1; массив 2). Здесь массив 1 и массив 2 – это перемножаемые матрицы. При этом количество столбцов аргумента массив 1 должно быть таким же, как количество строк аргумента массив 2, оба массива должны содержать только числа. Результатом (т.е. матрицей-произведением) является массив с таким же числом строк, как массив 1, и таким же числом столбцов, как массив 2. Пример 3. Найти произведение массивов Решение: 1. Введите матрицу А в диапазон А1:D3, а матрицу В в диапазон А4:В7. 2. Выделите блок ячеек под результирующую матрицу. Для этого необходимо найти размер матрицы-произведения. Ее размерность будет в данном примере 3*2. Выделите блок ячеек F1:G3. 3. Вызовите Мастер функций. В поле Категория выберите Математические, в поле Функции – имя функции МУМНОЖ. Нажмите ОК.
В появившемся диалоговом окне введите диапазоны массива 1 и массива 2 (соответственно А1:D3 и А4:В7). После этого нажмите сочетание клавиш CTRL+SHIFT+ENTER. 4. После этого в выделенном вами диапазоне должна появится матрица, которая равна произведению исходных матриц. Упражнения. 1. Найдите матрицу, обратную данной и определитель исходной матрицы. 2. Найдите матрицу, обратную данной и определитель исходной матрицы 3. Найти произведение матриц А*В, где 4. Вычислите А*В =
Решение1. На листе Excel составляем таблицу данных. Заполняем значение аргумента (в ячейки А1:А32) и значение функции (
Введем слово интеграл в ячейку А33 и в соседней ячейке формулы =0,1*, затем вызываем Мастер функций и в категории Математические выбираем функцию СУММ. Нажимаем ОК. В диалоговое окно Мастера функции вводим диапазон суммирования – значения функции (В2:В32). В ячейке В33 появляется приближенное значение интеграла (9,455). Ошибка в методе прямоугольников составила 0,455. Решение 2. Используем метод трапеции. Для этого в ячейку А34 введем слово интеграл 2. В соседнюю ячейку вводим формулу =0,1*((В2+В32)/2+) затем вызываем функцию СУММ. Нажимаем ОК. В диалоговое окно Мастера функции вводим диапазон суммирования – значения функции (В3:В31). В ячейке В34 появляется значение =9,005. В данном случае ошибка метода составляет 0,005, что вполне приемлемо.
Упражнения. Найти при помощи метода прямоугольника и трапеции определенные интегралы:
Решение. Этап 1.
Этап 2. 1. Вызываем процедуру Подбор параметров (Сервис – Подбор параметра).
2. В поле Установить в ячейке мышью указываем В2, в поле Значение с клавиатуры задаем 0 (правая часть уравнения), в поле Изменяя значение ячейки мышью указываем А2 (см. рис). 3. Щелкаем на кнопке ОК и получаем результат подбора, отображаемый в диалоговом окне Результат подбора параметра. Щелкаем на ОК, чтобы сохранить полученные значения ячеек, участвовавших в операции. При этом существует погрешность решения (вместо 0 в правой части уравнения получаем -0,00013).
Пример 2. Найти решение уравнения Решение. Уравнение имеет два корня. Решение начинаем с нахождения первого корня.
Упражнения.
Методические указания для выполнения лабораторных работ по теме Математика в «Excel» Оглавление Раздел 1. Аналитическая геометрия и линейная алгебра. 1 Тема 1.1 Декартова система координат. 1 Тема 1.2 Кривые второго порядка на плоскости. 2 Тема 1.3 Графическое решение системы уравнений. 2 Тема 1.4 Использование программы Excel в линейной алгебре. 3 Раздел 2. Элементы математического анализа. 4 Тема 2.1. Определенный интеграл. 5 Раздел 3. Задачи оптимизации. 6 Тема 3.1 Решение уравнения с одним неизвестным.. 6 Тема 3.2 Аппроксимация экспериментальных данных. 7
|
||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.77.149 (0.009 с.) |

 .
.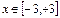 с шагом D=0,5.
с шагом D=0,5.
 с шагом D=0,25.
с шагом D=0,25. с шагом D=0,5.
с шагом D=0,5. в диапазоне
в диапазоне  с шагом D=0,2.
с шагом D=0,2. в диапазоне
в диапазоне 

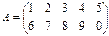
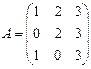
 и
и 





 ) (в ячейки В1:В32) (см. Декартова система координат, Пример 1).
) (в ячейки В1:В32) (см. Декартова система координат, Пример 1).
 с шагом Dх=0,1.
с шагом Dх=0,1.  с шагом Dх=0,1.
с шагом Dх=0,1. 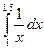 с шагом Dх=0,1.
с шагом Dх=0,1. 
 .
.




