
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретическое определение энергетических параметров очесывающего барабана и битера-отражателя очесывающего устройстваСодержание книги
Поиск на нашем сайте
Для определения энергетических параметров используем дифференциальные уравнения движения, в основу которых положена механическая модель, изображенная на рис. 2.17.
Рис. 2.17. Механическая модель очесывающего устройства: 1 – привод; 2 – редуктор; 3 – очесывающий барабан; 4 – битер-отражатель. При выводе дифференциальных уравнений динамики рассматриваемой механической системы примем следующие допущения: 1. Отдельные крупные конструктивные узлы 1, 2, 3, 4, соединенные с помощью цепей и ремней представляют абсолютно твердые тела, наделенные определенными массами с соответствующими моментами инерции I 1, I 2, I 3и I 4.. 2. Податливостью валов, цепей и ремней пренебрегаем, так как эти податливости несущественно влияют на абсолютные скорости вращения крупных конструктивных узлов, очесывающего барабана и битера-отражателя. 3. Гребенки – абсолютно твердые тела. 4. Внешним трением в подшипниках пренебрегаем. 5. Податливость в опорах отсутствует. 6. К ротору привода приложен внешний момент М 1 = М 1 (t) – известная функция времени, а к очесывающему барабану – момент сопротивления: МС = МС (ω 3) – известная функция угловой скорости. Обозначим абсолютные углы поворотов крупных конструктивных узлов через j 1(t) – привода, j 2(t) – редуктора, j 3(t) – очесывающего барабана и j 4(t) – битера-отражателя. На основании принципа Даламбера [109] построим следующую систему дифференциальных уравнений (2.28):
где
С целью определения угловых скоростей очесывающего барабана и битера-отражателя преобразуем систему (2.28) следующим образом. Сложим первое уравнение со вторым при r 1 = r 2 в результате получаем:
Полученное соотношение (2.29) умножим на r 4 ,а третье уравнение системы (2.27) на r 3
Сложив левые и правые части соотношений находим
Далее исключим неизвестные величины
здесь Для рассматриваемых переменных величин запишем такие кинематические зависимости:
Соотношения (2.32-2.34) позволяют получить дифференциальные уравнения, описывающие движения узлов I 4 и I 3.
Подставим (2.34) в (2.33), в результате чего найдем зависимость углового ускорения
Далее подставим (2.33) в (2.32) и выразив
Подставим (2.36), (2.35) и (2.34) в (2.31) получаем:
Перепишем полученное дифференциальное уравнение в следующем виде:
Введем такие обозначения:
С учетом данных обозначений получаем дифференциальное уравнение следующего вида:
где А – приведенный момент инерции системы к оси звена 4. Дифференциальное уравнение (2.37) описывает движение битера-отражателяв зависимости от характера изменения движущего момента Мд и момента сопротивления МС при счесывании, массовых Ij и геометрических ri параметров рассматриваемой системы. Аналогично получим дифференциальное уравнение, описывающее движение звена 3. С этой целью рассмотрим уравнение (2.33) и выразим согласно (2.36), (2.35) и (2.34) угловые ускорения
Подставляя выражения (2.38) в (2.31) получаем:
или:
Преобразуем (2.39), для чего введем такие обозначения:
тогда уравнение (2.39) примет следующий вид:
где А 1 – приведенный момент инерции системы к оси звена 3. Дифференциальное уравнение (2.40) описывает движение звена 3 в зависимости от движущего момента М 1(t), момента сопротивления МС и всех массовых, а также геометрических параметров рассматриваемой системы. Интегрирование уравнений (2.40) и (2.37) зависит от функциональной зависимости М С. Прежде, чем интегрировать эти уравнения при заданной функциональной зависимости М С, представим их в следующей форме:
где В дальнейшем примем, что момент сопротивления пропорционален первой степени угловой скорости вращения звена 3, т.е.:
Величина k зависит от многих физических и геометрических факторов. Подставим (2.42) во второе уравнение системы (2.41). В результате подстановки получаем следующее дифференциальное уравнение, описывающее движение очесывающего барабана,
где Обозначим
где n – коэффициент затухания. Полученное дифференциальное уравнение (2.43) второго порядка является линейным, неоднородным с постоянными коэффициентами относительно угла поворота Решение уравнения (2.43) складывается из суммы двух решений:
Однако нас интересует угловая скорость узла Для определения угловой скорости очесывающего барабана дифференциальное уравнение (2.43) представим в виде уравнения первого порядка относительно
Общее решение (2.25) согласно [27] представляется в форме:
где С – постоянная интегрирования, которая определяется из начального условия. Если n и К 1 – постоянные величины, тогда формула (2.46) принимает вид:
При установившемся режиме работы привода M 1
или интегрируя, получаем:
При t = 0,
Для переходного режима получаем:
Принимая вполне обоснованное условие равномерного движения комбайна t→∞, соответственно
Произведем обратную замену ранее принятых обозначений
Движущий момент при установившемся режиме принимаем, равным
где После преобразований, для определения мощности при очесе будем иметь
Момент сопротивления при очесе определим с учетом физико-механических свойств растений и стеблестоя в целом.
где Qоч – усилие при очесе, Н; rоб – радиус очесывающего барабана, м. Усилие при очесе определим из выражения
где Qоч 1 – усилие, необходимое для очеса одного соцветия, Н; к – число растений одновременно очесываемых одной гребенкой, шт.
где Fоч – площадь очеса одной гребенкой, м2; Н – густота стеблестоя, шт/м2.
где l – длина зуба очесывающей гребенки, м; Вр – ширина захвата очесывающего устройства, м. В результате подстановки (2.51-2.54) в (2.50) получим выражение для расчета мощности, необходимой на привод очесывающего барабана при очесывании растений.
С учётом начальной скорости V0 согласно разделу 2.3 можно записать
Но общая мощность на привод очесывающего барабана будет состоять из суммы [54]
где
где а – коэффициент, учитывающий массу барабана, b – коэффициент, учитывающий вентиляторную способность барабана,
Коэффициенты а и b определяются экспериментально. При работе очесывающего устройства функции битера-отражателя заключаются в отражении очесанного вороха и направлении его в сборник. Энергозатраты при этом незначительны и ими можно пренебречь. Поэтому мощность привода битера-отражателя определяется согласно уравнения [54] (2.57) с учетом сил сопротивления трения в подшипниках и воздушного потока. Расчет мощности на привод очесывающего барабана и битера-отражателя можно произвести только при конкретных условиях: параметрах стеблестоя и растений, геометрических и кинематических параметрах рабочих органов, которые определяются при изучении физико-механических свойств растений и проведении лабораторных исследований. Выводы по разделу 1. Согласно проведенного графоаналитического анализа работы очесывающего устройства с учетом геометрии стеблестоя определена методика расчета параметров, определяющих взаимное расположение битера-отражателя и очесывающего барабана и характерных точек кожуха битера-отражателя. 2. Рассмотрев основные функции битера-отражателя в технологическом процессе выделены его характерные зоны и определен его оптимальный радиус 0,19 м, который обеспечивает наилучшее условие вхождения растений в зону очеса и отражение продуктов обмолота в сборник.
3. Кинетическая энергия, которую сообщают продуктам обмолота рабочие органы очесывающего устройства вполне достаточна для преодоления сил тяжести и трения при движении зерна по отражающей поверхности кожуха до сборника зерна. 4. В результате проведения теоретических исследований определена методика для энергооценки битера-отражателя и очесывающего барабана. РАЗДЕЛ 3
|
|||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 309; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.173.30 (0.007 с.) |


 (2.28)
(2.28) – неизвестные натяжения соответствующих ведомых и ведущих ветвей цепей и ремня;
– неизвестные натяжения соответствующих ведомых и ведущих ветвей цепей и ремня; – радиусы зубчатых колес и шкивов.
– радиусы зубчатых колес и шкивов.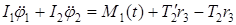 (2.29)
(2.29) .
. . (2.30)
. (2.30) и
и  . С этой целью соотношение (2.30) умножим на r 5, а четвертое уравнение системы (2.28) на r3r4 и в результате сложения получаем:
. С этой целью соотношение (2.30) умножим на r 5, а четвертое уравнение системы (2.28) на r3r4 и в результате сложения получаем: (2.31)
(2.31) .
.



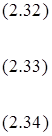
 от
от  .
. . (2.35)
. (2.35) через
через  . (2.36)
. (2.36) .
.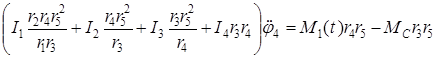 .
. .
. , (2.37)
, (2.37)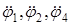 через
через  .
. . (2.38)
. (2.38)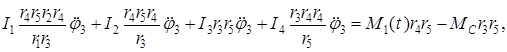 ,
, . (2.39)
. (2.39)


 , (2.40)
, (2.40) (2.41)
(2.41)
 (2.42)
(2.42) ,
,
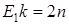 , тогда будем иметь:
, тогда будем иметь: , (2.43)
, (2.43) звена 3.
звена 3. , (2.44)
, (2.44)
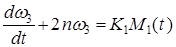 . (2.45)
. (2.45) , (2.46)
, (2.46) . (2.47)
. (2.47) , тогда
, тогда , (2.48)
, (2.48) .
. тогда
тогда , откуда
, откуда .
. .
. → 0. окончательно для ω 3 будем иметь выражение
→ 0. окончательно для ω 3 будем иметь выражение . (2.49)
. (2.49) ,
,  ,
,  ,
, 
 ,
,  .
. ,
, p – мощность, необходимая на привод очесывающего барабана для преодоления сил сопротивления при очесе растения на корню.
p – мощность, необходимая на привод очесывающего барабана для преодоления сил сопротивления при очесе растения на корню. . (2.50)
. (2.50) , (2.51)
, (2.51) , (2.52)
, (2.52)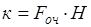 , (2.53)
, (2.53) , (2.54)
, (2.54)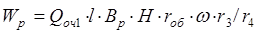 .
. (2.55)
(2.55) , (2.56)
, (2.56)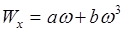 , (2.57)
, (2.57) – угловая скорость очесывающего барабана.
– угловая скорость очесывающего барабана.


