
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет емкости системы на единицу длины. Определение величины фиктивных зарядов и их положениеСодержание книги
Поиск на нашем сайте
Расположение фиктивного заряда найдем по схеме:
Рисунок 1.2 Расположение фиктивных зарядов Поверхности проводников и оболочки должны быть эквипотенциальными, т.е. должно выполняться равенство:
где rn – это расстояние от соответствующей оси до точки на проводнике или оболочке. Тогда получим систему:

Из системы находим выражения для S и а:
Емкость симметричной пары на единицу длины
Величина фиктивного заряда на единицу длины: τ = С×U = 7,7× 10-11 × 350 = 27,04 × 10-9 Кл/м
Расчет и построение графиков распределения напряженности электрического поля и потенциала системы проводников в плоскости KF Уравнение для потенциала в любой точке пространства:
С определяется из начальных условий, что φ(x,y) = 0 при x = 0, y = 0 → С = 0 В плоскости KF (как и на оси ОХ) y = 0, поэтому уравнение для потенциала перепишется так:
Закон распределения напряженности:
при y = 0:
Рисунок 1.3. График распределения потенциала электрического поля
Рисунок 1.4. График распределения напряженности электрического поля в плоскости KF
1.4 Расчет и построение графиков распределения напряженности электрического поля и потенциала системы проводников в плоскости
Рисунок 1.5. Схема из двух проводников
В плоскости y = –0,7 R2 уравнение для потенциала перепишется так:
а для напряженности
Модуль напряженности электрического поля в точке пространства с координатами (x, y) определяется следующим образом:
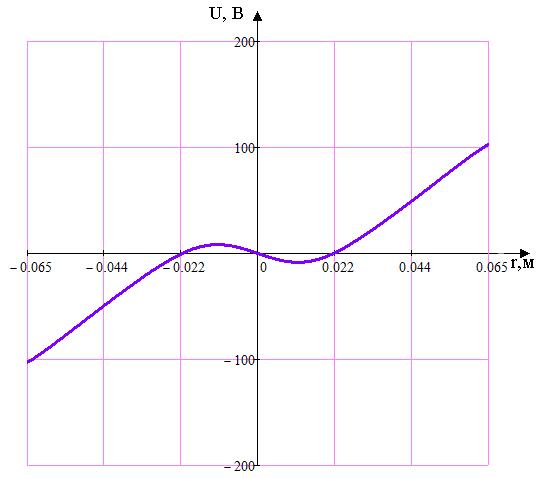
Рисунок 1.6. График распределения потенциала электрического поля
Рисунок 1.7 График распределения напряженности электрического поля в плоскости y= –0,7∙R2 Эквипотенциаль электрического поля с потенциалом kU Проведём эквипотенциаль с потенциалом, равным 0,4U, где U – приложенное напряжение. Система симметрична относительно оси ОХ, следовательно, координата Y центра окружности эквипотенциали равна 0. 0,18U = 63 В
имеем окружность радиуса 6,8 мм и с центром (–0,013;0).
Рисунок 1.8. Изображение эквипотенциали Выводы: - потенциал внутри маленьких проводников с радиусами R1 постоянен и для левого и правого проводников соответственно равен 175 В и –175 В; - напряженность поля внутри проводников с радиусами R1 равна нулю; - рассчитаны и построены графики распределения напряженности электрического поля и потенциала системы проводников в плоскости - эквипотенциаль есть окружность с центром в точке (–0,013;0) и радиуса Расчет магнитного поля проводника с электрическим током Исходные данные По круглому цилиндрическому проводнику протекает синусоидальный ток i=2,1∙sin wt, А. Радиус проводника R = 1,7 мм, удельная проводимость материала
Рисунок 2.1 Элемент цилиндрического проводника с электрическим током 1. Определить плотность тока и напряженность магнитного поля внутри проводника. Числовой ответ дать для точек, находящихся на расстоянии от оси провода r = 0; r = 0,2 R; r = 0,3 R; r = 0,5 R; r = 0,7 R; r = 0,9 R; r = 1.0 R при двух частотах: f = 200 Гц и nf = 26∙200 = 5200 Гц. 2. Построить графики зависимостей модулей плотности тока и напряженности магнитного поля от r. 3. Определить распределение напряженности магнитного поля снаружи проводника (расчеты осуществить в точках, находящихся на расстоянии от оси проводника соответственно r = 1.0 R; r = 1,2 R; r = 1,5 R; r = 2R; r = 5 R; r = 10 R; r = 15 R; r = 25 R; r = 50 R при двух частотах электрического тока: f и n f). Построить график распределения. 4. Определить величину потока вектора Пойнтинга (на единицу длины) внутри проводника с электрическим током. На чертеже указать направление вектора Пойнтинга. 5. Рассчитать и построить график распределения энергии магнитного поля снаружи проводника (расчеты осуществить в точках, указанных в п.3).
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 176; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.215.186 (0.006 с.) |





 = 44 мм
= 44 мм = 12 мм
= 12 мм = 7,7 × 10-11 Ф/м
= 7,7 × 10-11 Ф/м






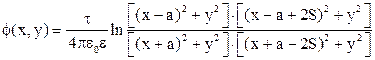 ,
,
 .
.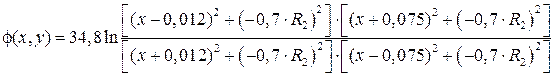


 .
.

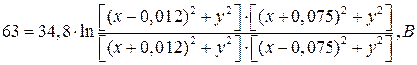 –
–




