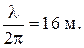Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет параметров магнитного экрана имеющего минимальные габаритные размеры и весСодержание книги
Поиск на нашем сайте
Определим значение относительной магнитной проницаемости при напряженности H0 = 59,6 A/м для различных видов стали и занесем данные в таблицу 3.2. Затем рассчитаем радиус внешнего экрана для каждого значения относительной магнитной проницаемости по формуле
и результаты вычислений также сведем в таблицу 3.2. Таблица 3.2 Определение минимальных параметров экрана
Анализируя полученные значения, определяем, что минимальные размеры соответствуют магнитной проницаемостью 394 для типа Электротехническая сталь. Таким образом, минимальный внешний радиус экрана Вес магнитного экрана равен
Выводы: - Оптимальные линейные размеры и вес магнитного экрана для материала сталь 10: r1 = 0,24 м, r2 = 0,25184 м, m = 35,7 кг; - Минимальные линейные размеры и вес магнитного экрана: r1 = 0,24 м, r2 = 0,24707, m = 21,1 кг; - Построили зависимость коэффициента экранирования от напряженности внешнего магнитного поля.
Расчет электромагнитного поля элементарного излучателя Исходные данные По отрезку прямолинейного провода длиной l = 76 мм проходит переменный ток i=0,46 sin(20∙106)t, A. Среда, окружающая провод, имеет
Рисунок 4.1. Исходная схема
4.2 Вывод аналитического выражения для определения напряженностей электрического и магнитного поля излучаемой электромагнитной волны в ближней и дальней зоне Составляющая векторного потенциала от элемента линейного тока
В переменном магнитном поле с учетом явления запаздывания имеем
Ток представим в показательной форме
или, если исключить множитель
Магнитную индукцию найдем из соотношения
для мгновенных значений
Напряженность магнитного поля равна
В соответствии с первым уравнением Максвелла
так как в рассматриваемой точке пространства
Тогда
Отсюда
Для мгновенных значений
В ближней зоне, где значение параметра R << λ/2π, для электромагнитного поля элемента проводника с током имеем следующие выражения:
Если значение параметра R >> λ/2π, то есть, имеем дело с дальней зоной, тогда для электромагнитного поля элемента проводника с током получаем:
Из условия ω = 20∙106 рад/с
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 198; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.206.196 (0.005 с.) |


 0,24707 м.
0,24707 м. кг.
кг. 80. Считать, что со средней точкой отрезка провода совмещено начало отсчета сферической системы координат и что ось отсчета углов совпадает с положительным направлением тока в проводе.
80. Считать, что со средней точкой отрезка провода совмещено начало отсчета сферической системы координат и что ось отсчета углов совпадает с положительным направлением тока в проводе.
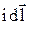 записывается как
записывается как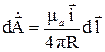

 , и для упрощения
, и для упрощения 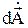 будем обозначать через
будем обозначать через 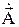 , тогда
, тогда
 ,
, .
. . Выражение для комплекса магнитной индукции в сферических координатах будет выглядеть следующим образом
. Выражение для комплекса магнитной индукции в сферических координатах будет выглядеть следующим образом ,
,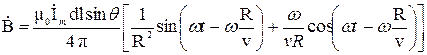 .
.
 ,
, =0, то
=0, то .
. .
.

 ,
, ,
, .
. ,
, .
.