Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Рекурсивные структуры данныхСодержание книги
Поиск на нашем сайте
Посмотрите на этот список: [5]. Это упро- щённая запись выражения 5:[]. С левой сторо- ны от оператора: ставится значение, с правой стороны – список (в нашем случае пустой). Как насчёт списка [4,5]? Его можно переписать так: 4:(5:[]). Смотря на первый оператор:, мы видим, что слева от него – всё так же значение, а справа – список (5:[]). То же можно сказать и в отношении списка 3:(4:(5:6:[])); это выражение можно переписать и как 3:4:5:6:[] (поскольку опе- ратор: правоассоциативен), и как [3,4,5,6]. Мы можем сказать, что список может быть пустым или это мо- жет быть элемент, присоединенный с помощью оператора: к дру- гому списку (который в свою очередь может быть пустым или нет). Ну что ж, давайте используем алгебраические типы данных,
чтобы создать наш собственный список. data List a = Empty | Cons a (List a) deriving (Show, Read, Eq, Ord)
Это можно прочитать почти как наше определение списка в од-
ном из предыдущих разделов. Это либо пустой список, либо ком- бинация некоторого значения («головы») и собственно списка («хвоста»). Если такая формулировка трудна для понимания, то с ис- пользованием синтаксиса записей она будет восприниматься легче. data List a = Empty | Cons { listHead:: a, listTail:: List a} deriving (Show, Read, Eq, Ord)
Конструктор Cons может вызвать недоумение. Идентификатор Cons – всего лишь альтернативное обозначение:. Как вы видите, в списках оператор: – это просто конструктор, который прини- мает значение и список и возвращает список. Мы можем исполь- зовать и наш новый тип для задания списка! Другими словами, он имеет два поля: первое типа а и второе типа [a]. ghci> Empty Empty ghci> 5 `Cons` Empty Cons 5 Empty ghci> 4 `Cons` (5 `Cons` Empty) Cons 4 (Cons 5 Empty) ghci> 3 `Cons` (4 `Cons` (5 `Cons` Empty))
Cons 3 (Cons 4 (Cons 5 Empty)) Мы вызываем конструктор Cons как инфиксный оператор, что- бы наглядно показать, что мы используем его вместо оператора:. Конструктор Empty играет роль пустого списка [], и выражение 4 `Cons` (5 `Cons` Empty) подобно выражению 4:(5:[]).
Улучшение нашего списка
Мы можем определить функцию как инфиксную по умолчанию, если её имя состоит только из специальных символов. То же самое можно сделать и с конструкторами, поскольку это просто функции, возвращающие тип данных. Смотрите: infixr 5:–:
data List a = Empty | a:–: (List a) deriving (Show, Read, Eq, Ord) Первое: мы использовали новую синтаксическую конструк- цию, декларацию ассоциативности функции. Если мы определя- ем функции как операторы, то можем присвоить им значение
ассоциативности, но не обязаны этого делать. Ассоциативность показывает, какова приоритетность оператора и является ли он лево- или правоассоциативным. Например, ассоциативность ум- ножения – infixl 7 *, ассоциативность сложения – infixl 6. Это значит, что оба оператора левоассоциативны, выражение 4 * 3 * 2 означает ((4 * 3) * 2), умножение имеет более высокий приоритет, чем сложение, поэтому выражение 5 * 4 + 3 означает (5 * 4) + 3.
Следовательно, ничто не мешает записать a:–: (List a) вместо Cons a (List a). Теперь мы можем представлять списки нашего ново- го спискового типа таким образом: ghci> 3:-: 4:-: 5:-: Empty 3:-: (4:-: (5:-: Empty)) ghci> let a = 3:-: 4:-: 5:-: Empty ghci> 100:-: a
100:-: (3:-: (4:-: (5:-: Empty)) Напишем функцию для сложения двух списков. Вот как опера- тор ++ определён для обычных списков:
infixr 5 ++ (++):: [a] –> [a] –> [a] [] ++ ys = ys
(x:xs) ++ ys = x: (xs ++ ys) Давайте просто передерём это объявление для нашего списка!
Назовём нашу функцию ^++: infixr 5 ++ (^++):: List a –> List a –> List a Empty ^++ ys = ys
(x:–: xs) ++ ys = x:–: (xs ++ ys) И посмотрим, как это работает...
ghci> let a = 3:-: 4:-: 5:-: Empty ghci> let b = 6:-: 7:-: Empty ghci> a ++ b
3:-: (4:-: (5:-: (6:-: (7:-: Empty)))) Очень хорошо. Если бы мы хотели, мы могли бы реализовать все функции для работы со списками и для нашего спискового типа.
Обратите внимание, как мы выполняли сопоставление с образ- цом по (x:–: xs). Это работает, потому что на самом деле данная операция сопоставляет конструкторы. Мы можем сопоставлять по конструктору:–: потому, что это конструктор для нашего собс- твенного спискового типа, так же как можем сопоставлять и по конструктору:, поскольку это конструктор встроенного списко- вого типа. Так как сопоставление производится только по конс- трукторам, можно искать соответствие по образцам, подобным (x:–: xs), или константам, таким как 8 или 'a', поскольку на са- мом деле они являются конструкторами для числового и символь- ного типов1.
Вырастим-ка дерево
8 больше 7, снова выберем правое поддерево. В резуль- тате элемент найдётся всего за три операции сравнения! Если мы бы искали в обычном списке (или в сильно разба- лансированном дереве), пот- ребовалось бы до семи срав- нений вместо трёх для поиска того же элемента. 1 На самом деле в синтаксисе языка Haskell имеются ещё так называемые (n + k)-об- разцы. Впрочем, большая часть сообщества языка их отвергает. – Прим. ред. ПРИМЕЧАНИЕ. Множества и отображения из модулей Data.Set и Data.Map реализованы с помощью деревьев, но вместо обычных бинарных поисковых деревьев они используют сбалансирован- ные поисковые деревья. Дерево называется сбалансирован- ным, если высоты его левого и правого поддеревьев примерно равны. Это условие ускоряет поиск по дереву. В наших приме- рах мы реализуем обычные поисковые деревья.
Вот что мы собираемся сказать: дерево – это или пустое дерево, или элемент, который содержит некоторое значение и два поддере- ва. Такая формулировка идеально соответствует алгебраическому типу данных. data Tree a = EmptyTree | Node a (Tree a) (Tree a) deriving (Show)
Что ж, отлично. Вместо того чтобы вручную создавать дерево, мы напишем функцию, которая принимает дерево и элемент и до- бавляет элемент к дереву. Мы будем делать это, сравнивая встав- ляемый элемент с корневым. Если вставляемый элемент меньше корневого – идём налево, если больше – направо. Эту же операцию продолжаем для каждого последующего узла дерева, пока не до- стигнем пустого дерева. После этого мы добавляем новый элемент вместо пустого дерева. В языках, подобных С, мы бы делали это, изменяя указатели и значения внутри дерева. В Haskell мы на самом деле не можем из- менять наше дерево – придётся создавать новое поддерево каждый раз, когда мы переходим к левому или правому поддереву. Таким образом, в конце функции добавления мы вернём полностью но- вое дерево, потому что в языке Haskell нет концепции указателей, есть только значения. Следовательно, тип функции для добавле- ния элемента будет примерно следующим: a –> Tree a – > Tree a. Она принимает элемент и дерево и возвращает новое дерево с уже до- бавленным элементом. Это может показаться неэффективным, но язык Haskell умеет организовывать совместное владение большей частью поддеревьев старым и новым деревьями.
Итак, напишем две функции. Первая будет вспомогательной функцией для создания дерева, состоящего из одного элемента; вторая будет вставлять элемент в дерево. singleton:: a –> Tree a singleton x = Node x EmptyTree EmptyTree
treeInsert:: (Ord a) => a –> Tree a –> Tree a treeInsert x EmptyTree = singleton x treeInsert x (Node a left right) | x == a = Node x left right | x < a = Node a (treeInsert x left) right
| x > a = Node a left (treeInsert x right) Функция singleton служит для создания узла, который хранит некоторое значение и два пустых поддерева. В функции для добав- ления нового элемента в дерево мы вначале обрабатываем гранич- ное условие. Если мы достигли пустого поддерева, это значит, что мы в нужном месте нашего дерева, и вместо пустого дерева поме- щаем одноэлементное дерево, созданное из нашего значения. Если мы вставляем не в пустое дерево, следует кое-что проверить. Пер- вое: если вставляемый элемент равен корневому элементу – просто возвращаем дерево текущего элемента. Если он меньше, возвраща- ем дерево, которое имеет то же корневое значение и то же правое поддерево, но вместо левого поддерева помещаем дерево с добав- ленным элементом. Так же (но с соответствующими поправками) обстоит дело, если значение больше, чем корневой элемент.
Следующей мы напишем функцию для проверки, входит ли не- который элемент в наше дерево или нет. Для начала определим ба- зовые случаи. Если мы ищем элемент в пустом дереве, его там опре- делённо нет. Заметили – такой же базовый случай мы использовали для поиска элемента в списке? Если мы ищем в пустом списке, то ничего не найдём. Если ищем не в пустом дереве, надо проверить несколько условий. Если элемент в текущем корне равен тому, что мы ищем, – отлично. Ну а если нет, тогда как быть?.. Мы можем из- влечь пользу из того, что все элементы в левом поддереве меньше корневого элемента. Поэтому, если искомый элемент меньше кор- невого, начинаем искать в левом поддереве. Если он больше – ищем в правом поддереве. treeElem:: (Ord a) => a –> Tree a –> Bool treeElem x EmptyTree = False treeElem x (Node a left right) | x == a = True | x < a = treeElem x left
| x > a = treeElem x right
Всё, что нам нужно было сделать, – переписать предыдущий па- раграф в коде. Давайте немного «погоняем» наши деревья. Вместо того чтобы вручную задавать деревья (а мы можем!), будем исполь- зовать свёртку для того, чтобы создать дерево из списка. Запомни- те: всё, что обходит список элемент за элементом и возвращает не- которое значение, может быть представлено свёрткой. Мы начнём с пустого дерева и затем будем проходить список справа налево и вставлять элемент за элементом в дерево-аккумулятор. ghci> let nums = [8,6,4,1,7,3,5] ghci> let numsTree = foldr treeInsert EmptyTree nums ghci> numsTree Node 5 (Node 3 (Node 1 EmptyTree EmptyTree) (Node 4 EmptyTree EmptyTree) ) (Node 7 (Node 6 EmptyTree EmptyTree) (Node 8 EmptyTree EmptyTree)
) ПРИМЕЧАНИЕ. Если вы вызовете этот код в интерпретаторе GHCi, то в качестве вывода будет одна длинная строка. Здесь она разбита на несколько строк, иначе она бы вышла за пределы страницы. В этом вызове функции foldr функция treeInsert играет роль функции свёртки (принимает дерево и элемент списка и создаёт новое дерево); EmptyTree – стартовое значение аккумулятора. Пара- метр nums – это, конечно же, список, который мы сворачиваем.
Если напечатать дерево на консоли, мы получим не очень-то легко читаемое выражение, но если постараться, можно уловить структуру. Мы видим, что корневое значение – 5; оно имеет два поддерева, в одном из которых корневым элементом является 3, а в другом – 7, и т. д. ghci> 8 `treeElem` numsTree True ghci> 100 `treeElem` numsTree False ghci> 1 `treeElem` numsTree
True
ghci> 10 `treeElem` numsTree False Проверка на вхождение также работает отлично. Классно! Как вы можете видеть, алгебраические типы данных в языке Haskell нереально круты. Мы можем использовать их для создания чего угодно – от булевских значений и перечислимого типа для дней недели до бинарных поисковых деревьев и даже большего!
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.01 с.) |

 Как мы уже видели, конструкторы алгебраи- ческих типов данных могут иметь несколько полей (или не иметь вовсе), и у каждого поля должен быть конкретный тип. Принимая это во внимание, мы можем создать тип, конструк- тор которого имеет поля того же самого типа! Таким образом мы можем создавать рекурсив- ные типы данных, где одно значение некоторо- го типа содержит другие значения этого типа, а они, в свою очередь, содержат ещё значения того же типа, и т. д.
Как мы уже видели, конструкторы алгебраи- ческих типов данных могут иметь несколько полей (или не иметь вовсе), и у каждого поля должен быть конкретный тип. Принимая это во внимание, мы можем создать тип, конструк- тор которого имеет поля того же самого типа! Таким образом мы можем создавать рекурсив- ные типы данных, где одно значение некоторо- го типа содержит другие значения этого типа, а они, в свою очередь, содержат ещё значения того же типа, и т. д.





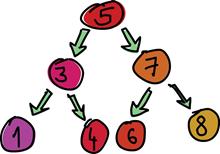 Теперь мы собираемся реализовать бинарное поисковое дерево. Если вам не знакомы поисковые деревья из языков наподобие С, вот что они представляют собой: элемент указывает на два других элемента, один из которых правый, другой – левый. Элемент сле- ва – меньше, чем текущий, элемент справа – больше. Каждый из этих двух элементов также может ссылаться на два других элемента (или на один, или не ссылаться вообще). Получается, что каждый элемент может иметь до двух поддеревьев. Бинарные поисковые деревья удобны тем, что мы знаем, что все элементы в левом подде- реве элемента со значением, скажем, пять, будут меньше пяти. Эле- менты в правом поддереве будут больше пяти. Таким образом, если нам надо найти 8 в нашем дереве, мы начнём с пятёрки, и так как 8 больше 5, будем проверять правое поддерево. Теперь проверим узел со значением 7, и так как
Теперь мы собираемся реализовать бинарное поисковое дерево. Если вам не знакомы поисковые деревья из языков наподобие С, вот что они представляют собой: элемент указывает на два других элемента, один из которых правый, другой – левый. Элемент сле- ва – меньше, чем текущий, элемент справа – больше. Каждый из этих двух элементов также может ссылаться на два других элемента (или на один, или не ссылаться вообще). Получается, что каждый элемент может иметь до двух поддеревьев. Бинарные поисковые деревья удобны тем, что мы знаем, что все элементы в левом подде- реве элемента со значением, скажем, пять, будут меньше пяти. Эле- менты в правом поддереве будут больше пяти. Таким образом, если нам надо найти 8 в нашем дереве, мы начнём с пятёрки, и так как 8 больше 5, будем проверять правое поддерево. Теперь проверим узел со значением 7, и так как