
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Класс MonadPlus и функция guardСодержание книги
Поиск на нашем сайте
Генераторы списков позволяют нам фильтровать наши выходные данные. Например, мы можем отфильтровать список чисел в поис- ке только тех из них, которые содержат цифру 7: ghci> [x | x <– [1..50], '7' `elem` show x] [7,17,27,37,47]
Мы применяем функцию show к параметру x чтобы превратить наше число в строку, а затем проверяем, является ли символ '7' час- тью этой строки. Чтобы увидеть, как фильтрация в генераторах списков преоб- разуется в списковую монаду, мы должны рассмотреть функцию guard и класс типов MonadPlus. Класс типов MonadPlus предназначен для монад, которые также могут вести себя как моноиды. Вот его определение:
class Monad m => MonadPlus m where mzero:: m a
mplus:: m a –> m a –> m a Функция mzero является синонимом функции mempty из класса типов Monoid, а функция mplus соответствует функции mappend. По- скольку списки являются моноидами, а также монадами, их можно сделать экземпляром этого класса типов:
instance MonadPlus [] where mzero = []
mplus = (++) Для списков функция mzero представляет недетерминирован- ное вычисление, которое вообще не имеет результата – неуспешно окончившееся вычисление. Функция mplus сводит два недетерми- нированных значения в одно. Функция guard определена следую- щим образом:
guard:: (MonadPlus m) => Bool –> m () guard True = return ()
guard False = mzero Функция guard принимает значение типа Bool. Если это значе- ние равно True, функция guard берёт пустой кортеж () и помещает его в минимальный контекст, который по-прежнему является ус- пешным. Если значение типа Bool равно False, функция guard со- здаёт монадическое значение с неудачей в вычислениях. Вот эта функция в действии:
ghci> guard (5 > 2):: Maybe () Just () ghci> guard (1 > 2):: Maybe () Nothing ghci> guard (5 > 2):: [()] [()]
ghci> guard (1 > 2):: [()] [] Выглядит интересно, но чем это может быть полезно? В списко- вой монаде мы используем её для фильтрации недетерминирован- ных вычислений:
ghci> [1..50] >>= (\x –> guard ('7' `elem` show x) >> return x)
[7,17,27,37,47] Результат аналогичен тому, что был возвращен нашим преды- дущим генератором списка. Как функция guard достигла этого? Давайте сначала посмотрим, как она функционирует совместно с операцией >>:
ghci> guard (5 > 2) >> return "клёво":: [String] ["клёво"]
ghci> guard (1 > 2) >> return "клёво":: [String] [] Если функция guard срабатывает успешно, результатом, находя- щимся в ней, будет пустой кортеж. Поэтому дальше мы используем операцию >>, чтобы игнорировать этот пустой кортеж и предоста- вить что-нибудь другое в качестве результата. Однако если функ- ция guard не срабатывает успешно, функция return впоследствии тоже не сработает успешно, потому что передача пустого списка функции с помощью операции >>= всегда даёт в результате пустой список. Функция guard просто говорит: «Если это значение типа Bool равно False, верни неуспешное окончание вычислений прямо здесь. В противном случае создай успешное значение, которое со- держит в себе значение-пустышку ()». Всё, что она делает, – позво- ляет вычислению продолжиться.
Вот предыдущий пример, переписанный в нотации do: sevensOnly:: [Int] sevensOnly = do x <– [1..50]
guard ('7' `elem` show x) return x Если бы мы забыли представить образец x в качестве оконча- тельного результата, используя функцию return, то результирую- щий список состоял бы просто из пустых кортежей. Вот определе- ние в форме генератора списка:
ghci> [x | x <– [1..50], '7' `elem` show x] [7,17,27,37,47] Поэтому фильтрация в генераторах списков – это то же самое, что использование функции guard.
Ход конём
Создадим синоним типа для текущей позиции коня на шахмат- ной доске. type KnightPos = (Int, Int)
Теперь предположим, что конь начинает движение с позиции (6, 2). Может ли он добраться до (6, 1) именно за три хода? Какой ход лучше сделать следующим из его нынешней позиции? Я знаю: как насчёт их всех?! К нашим услугам недетерминированность, по- этому вместо того, чтобы выбрать один ход, давайте просто выбе- рем их все сразу! Вот функция, которая берёт позицию коня и воз- вращает все его следующие ходы: moveKnight:: KnightPos –> [KnightPos] moveKnight (c,r) = do
(c',r') <– [(c+2,r-1),(c+2,r+1),(c-2,r-1),(c-2,r+1) ,(c+1,r-2),(c+1,r+2),(c-1,r-2),(c-1,r+2) ]
guard (c' `elem` [1..8] && r' `elem` [1..8]) return (c',r') Конь всегда может перемещаться на одну клетку горизонтально или вертикально и на две клетки вертикально или горизонтально, причём каждый его ход включает движение и по горизонтали, и по вертикали. Пара (c', r') получает каждое значение из списка пере- мещений, а затем функция guard заботится о том, чтобы новый ход, а именно пара (c', r'), был в пределах доски. Если движение выхо- дит за доску, она возвращает пустой список, что приводит к неуда- че, и вызов return (c', r') не обрабатывается для данной позиции.
Эта функция может быть записана и без использования списков в качестве монад. Вот как записать её с использованием функции filter: moveKnight:: KnightPos –> [KnightPos] moveKnight (c,r) = filter onBoard [(c+2,r-1),(c+2,r+1),(c-2,r-1),(c-2,r+1) ,(c+1,r-2),(c+1,r+2),(c-1,r-2),(c-1,r+2) ]
where onBoard (c,r) = c `elem` [1..8] && r `elem` [1..8] Обе версии делают одно и то же, так что выбирайте ту, которая кажется вам лучше. Давайте опробуем функцию:
ghci> moveKnight (6, 2) [(8,1),(8,3),(4,1),(4,3),(7,4),(5,4)] ghci> moveKnight (8, 1)
[(6,2),(7,3)] Работает чудесно! Мы берём одну позицию и просто выполня- ем все возможные ходы сразу, так сказать.
Поэтому теперь, когда у нас есть следующая недетерминиро- ванная позиция, мы просто используем операцию >>=, чтобы пере- дать её функции moveKnight. Вот функция, принимающая позицию и возвращающая все позиции, которые вы можете достигнуть из неё в три хода: in3:: KnightPos –> [KnightPos]
in3 start = do
first <– moveKnight start second <– moveKnight first moveKnight second Если вы передадите ей пару (6, 2), результирующий список бу- дет довольно большим. Причина в том, что если есть несколько пу- тей достигнуть определённой позиции в три хода, ход неожиданно появляется в списке несколько раз.
Вот предшествующий код без использования нотации do: in3 start = return start >>= moveKnight >>= moveKnight >>= moveKnight
Однократное использование операции >>= даёт нам все воз- можные ходы с начала. Когда мы используем операцию >>= второй раз, то для каждого возможного первого хода вычисляется каждый возможный следующий ход; то же самое верно и в отношении пос- леднего хода. Помещение значения в контекст по умолчанию с применени- ем к нему функции return, а затем передача его функции с исполь- зованием операции >>= – то же самое, что и обычное применение функции к данному значению; но мы сделали это здесь, во всяком случае, ради стиля.
Теперь давайте создадим функцию, которая принимает две по- зиции и сообщает нам, можем ли мы попасть из одной в другую ров- но в три хода: canReachIn3:: KnightPos –> KnightPos –> Bool canReachIn3 start end = end `elem` in3 start
Мы производим все возможные позиции в пределах трёх ходов, а затем проверяем, находится ли среди них искомая.
Вот как проверить, можем ли мы попасть из (6,2) в (6,1) в три хода: ghci> (6, 2) `canReachIn3` (6, 1) True
Да! Как насчёт из (6, 2) в (7, 3)? ghci> (6, 2) `canReachIn3` (7, 3) False
Нет! В качестве упражнения вы можете изменить эту функцию так, чтобы она показывала вам ходы, которые нужно совершить, когда вы можете достигнуть одной позиции из другой. В главе 14 вы увидите, как изменить эту функцию, чтобы также передавать ей число ходов, которые необходимо произвести, вместо того чтобы кодировать это число жёстко, как сейчас.
Законы монад Так же, как в отношении функторов и аппликативных функторов, в отношении монад действует несколько законов, которым должны подчиняться все экземпляры класса Monad. Даже если что-то сделано экземпляром класса типов Monad, это ещё не означает, что на самом деле перед нами монада. Чтобы тип по-настоящему был монадой, для него должны выполняться законы монад. Эти законы позволяют нам делать обоснованные предположения о типе и его поведении.
экземпляр класса типов Monad, мы должны обладать достаточной уверенностью в том, что с выполнением законов монад для этого типа всё хорошо. Можно полагаться на то, что типы в стандартной библиотеке удовлетворяют законам, но когда мы перейдем к созда- нию собственных монад, нам необходимо будет проверять выпол- нение законов вручную. Впрочем, не беспокойтесь – эти законы совсем не сложны!
Левая единица Первый закон монад утверждает, что если мы берём значение, по- мещаем его в контекст по умолчанию с помощью функции return, а затем передаём его функции, используя операцию >>=, это равно- значно тому, как если бы мы просто взяли значение и применили
к нему функцию. Говоря формально, return x >>= f – это то же самое, что и f x. Если вы посмотрите на монадические значения как на значе- ния с контекстом и на функцию return как на получение значения и помещение его в минимальный контекст по умолчанию, который по-прежнему возвращает это значение в качестве результата фун- кции, то закон имеет смысл. Если данный контекст действитель- но минимален, передача этого монадического значения функции не должна сильно отличаться от простого применения функции к обычному значению – и действительно, вообще ничем не отли- чается.
Функция return для монады Maybe определена как вызов конс- труктора Just. Вся суть монады Maybe состоит в возможном неуспе- хе в вычислениях, и если у нас есть значение, которое мы хотим поместить в такой контекст, есть смысл в том, чтобы обрабатывать его как успешное вычисление, поскольку мы знаем, каким является значение. Вот некоторые примеры использования функции return с типом Maybe: ghci> return 3 >>= (\x –> Just (x+100000)) Just 100003
ghci> (\x –> Just (x+100000)) 3 Just 100003 Для списковой монады функция return помещает что-либо в одноэлементный список. Реализация операции >>= для списков проходит по всем значениям в списке и применяет к ним функцию. Однако, поскольку в одноэлементном списке лишь одно значение, это аналогично применению функции к данному значению:
ghci> return "WoM" >>= (\x –> [x,x,x]) ["WoM","WoM","WoM"] ghci> (\x –> [x,x,x]) "WoM"
["WoM","WoM","WoM"] Вы знаете, что для монады IO использование функции return создаёт действие ввода-вывода, которое не имеет побочных эффек- тов, но просто возвращает значение в качестве своего результата. Поэтому вполне логично, что этот закон выполняется также и для монады IO.
Правая единица Второй закон утверждает, что если у нас есть монадическое зна- чение и мы используем операцию >>= для передачи его функции return, результатом будет наше изначальное монадическое значе- ние. Формально m >>= return является не чем иным, как просто m. Этот закон может быть чуть менее очевиден, чем первый. Да- вайте посмотрим, почему он должен выполняться. Когда мы пере- даём монадические значения функции, используя операцию >>=, эти функции принимают обычные значения и возвращают монади- ческие. Функция return тоже является такой, если вы рассмотрите её тип. Функция return помещает значение в минимальный контекст, который по-прежнему возвращает это значение в качестве своего результата. Это значит, что, например, для типа Maybe она не вносит никакого неуспеха в вычислениях; для списков – не вносит какую- либо дополнительную недетерминированность.
Вот пробный запуск для нескольких монад: ghci> Just "двигайся дальше" >>= (\x –> return x) Just "двигайся дальше" ghci> [1,2,3,4] >>= (\x –> return x) [1,2,3,4]
ghci> putStrLn "Вах!" >>= (\x –> return x) Вах! В этом примере со списком реализация операции >>= выглядит следующим образом:
xs >>= f = concat (map f xs) Поэтому когда мы передаём список [1,2,3,4] функции return, сначала она отображает [1,2,3,4], что в результате даёт список списков [[1],[2],[3],[4]]. Затем это конкатенируется, и мы полу- чаем наш изначальный список. Левое тождество и правое тождество являются, по сути, зако- нами, которые описывают, как должна вести себя функция return. Это важная функция для превращения обычных значений в мона- дические, и было бы нехорошо, если бы монадическое значение, которое она произвела, имело больше, чем необходимый мини- мальный контекст.
Ассоциативность Последний монадический закон говорит, что когда у нас есть цепоч- ка применений монадических функций с помощью операции >>=, не должно иметь значения то, как они вложены. В формальной за- писи выполнение (m >>= f) >>= g – точно то же, что и выполнение m >>= (\x –> f x >>= g). Гм-м, что теперь тут происходит? У нас есть одно монадическое значение, m, и две монадические функции, f и g. Когда мы выполняем выражение (m >>= f) >>= g, то передаём значение m в функцию f, что даёт в результате монадическое значение. Затем мы передаём это новое монадическое значение функции g. В выражении m >>= (\x –> f x >>= g) мы берём монадическое значение и передаём его функции, которая передаёт результат применения f x функции g. Нелегко уви- деть, почему обе эти записи равны, так что давайте взглянем на при- мер, который делает это равенство немного более очевидным.
Помните нашего канатоходца Пьера, который пытался удер- жать равновесие, в то время как птицы приземлялись на его балан- сировочный шест? Чтобы симулировать приземление птиц на ба- лансировочный шест, мы создали цепочку из нескольких функций, которые могли вызывать неуспешное окончание вычислений: ghci> return (0, 0) >>= landRight 2 >>= landLeft 2 >>= landRight 2
Just (2,4) Мы начали со значения Just (0, 0), а затем связали это значе- ние со следующей монадической функцией landRight 2. Результатом было другое монадическое значение, связанное со следующей мо- надической функцией, и т. д. Если бы надлежало явно заключить это в скобки, мы написали бы следующее:
ghci> ((return (0, 0) >>= landRight 2) >>= landLeft 2) >>= landRight 2
Just (2,4) Но мы также можем записать инструкцию вот так:
return (0, 0) >>= (\x –> landRight 2 x >>= (\y –> landLeft 2 y >>= (\z –> landRight 2 z))) Вызов return (0, 0) – то же самое, что Just (0, 0), и когда мы пере- даём это анонимной функции, образец x принимает значение (0, 0).
Функция landRight принимает количество птиц и шест (кортеж, содержащий числа) – и это то, что ей передаётся. В результате мы имеем значение Just (0, 2), и, когда передаём его следующей ано- нимной функции, образец y становится равен (0, 2). Это продол- жается до тех пор, пока последнее приземление птицы не вернёт в качестве результата значение Just (2, 4), что в действительности является результатом всего выражения.
Поэтому неважно, как у вас вложена передача значений монади- ческим функциям. Важен их смысл. Давайте рассмотрим ещё один способ реализации этого закона. Предположим, мы производим композицию двух функций, f и g: (.):: (b –> c) –> (a –> b) –> (a –> c)
f. g = (\x –> f (g x)) Если функция g имеет тип a –> b и функция f имеет тип b –> c, мы компонуем их в новую функцию типа a –> c, чтобы её параметр передавался между этими функциями. А что если эти две функ- ции – монадические? Что если возвращаемые ими значения были бы монадическими? Если бы у нас была функция типа a –> m b, мы не могли бы просто передать её результат функции типа b –> m c, пото- му что эта функция принимает обычное значение b, не монадичес- кое. Чтобы всё-таки достичь нашей цели, можно воспользоваться операцией <=<:
(<=<):: (Monad m) => (b –> m c) –> (a –> m b) –> (a –> m c) f <=< g = (\x –> g x >>= f) Поэтому теперь мы можем производить композицию двух мо- надических функций:
ghci> let f x = [x,-x] ghci> let g x = [x*3,x*2] ghci> let h = f <=< g ghci> h 3
[9,-9,6,-6] Ладно, всё это здорово. Но какое это имеет отношение к зако- ну ассоциативности? Просто, когда мы рассматриваем этот закон как закон композиций, он утверждает, что f <=< (g <=< h) должно быть равнозначно (f <=< g) <=< h. Это всего лишь ещё один способ доказать, что для монад вложенность операций не должна иметь значения.
Если мы преобразуем первые два закона так, чтобы они исполь- зовали операцию <=<, то закон левого тождества утверждает, что для каждой монадической функции f выражение f <=< return озна- чает то же самое, что просто вызвать f. Закон правого тождества говорит, что выражение return <=< f также ничем не отличается от простого вызова f. Это подобно тому, как если бы f являлась обыч- ной функцией, и тогда (f. g). h было бы аналогично f. (g. h), вы- ражение f. id – всегда аналогично f, и выражение id. f тоже ничем не отличалось бы от вызова f. В этой главе мы в общих чертах ознакомились с монадами и изу- чили, как работают монада Maybe и списковая монада. В следующей главе мы рассмотрим целую кучу других крутых монад, а также со- здадим нашу собственную.
ЕЩЁ НЕМНОГО МОНАД Мы видели, как монады могут быть использованы для получения значений с контекстами и применения их к функциям и как исполь- зование оператора >>= или нотации do позволяет нам сфокусиро- ваться на самих значениях, в то время как контекст обрабатывается за нас.
В этой главе мы узнаем ещё о несколь- ких монадах. Мы увидим, как они могут сделать наши программы понятнее, поз- воляя нам обрабатывать все типы значе- ний как монадические значения. Иссле- дование ряда примеров также укрепит наше понимание монад. Все монады, которые нам предстоит рассмотреть, являются частью пакета mtl. В языке Haskell пакетом является совокуп- ность модулей. Пакет mtl идёт в поставке
с Haskell Platform, так что он у вас, вероятно, уже есть. Чтобы про- верить, так ли это, выполните команду ghc-pkg list в командной строке. Эта команда покажет, какие пакеты для языка Haskell у вас уже установлены; одним из таких пакетов должен являться mtl, за названием которого следует номер версии.
Writer? Я о ней почти не знаю! Итак, мы зарядили наш пистолет монадой Maybe, списковой мона- дой и монадой IO. Теперь давайте поместим в патронник монаду Writer и посмотрим, что произойдёт, когда мы выстрелим ею! Между тем как Maybe предназначена для значений с добав- ленным контекстом неуспешно оканчивающихся вычислений, а список – для недетерминированных вычислений, монада Writer предусмотрена для значений, к которым присоединено другое зна- чение, ведущее себя наподобие журнала. Монада Writer позволяет нам производить вычисления, в то же время обеспечивая слияние всех журнальных значений в одно, которое затем присоединяется к результату.
Например, мы могли бы снабдить наши значения строками, которые объясняют, что происходит, возможно, для отладочных целей. Рассмотрите функцию, которая принимает число бандитов в банде и сообщает нам, является ли эта банда крупной. Это очень простая функция: isBigGang:: Int –> Bool isBigGang x = x > 9
Ну а что если теперь вместо возвращения значения True или False мы хотим, чтобы функция также возвращала строку журнала, которая сообщает, что она сделала? Что ж, мы просто создаём эту строку и возвращаем её наряду с нашим значением Bool: isBigGang:: Int –> (Bool, String)
isBigGang x = (x > 9, "Размер банды сравнён с 9.") Так что теперь вместо того, чтобы просто вернуть значение типа Bool, мы возвращаем кортеж, первым компонентом которого является само значение, а вторым компонентом – строка, сопутс- твующая этому значению. Теперь у нашего значения появился неко- торый добавленный контекст. Давайте опробуем функцию:
ghci> isBigGang 3 (False,"Размер банды сравнён с 9.") ghci> isBigGang 30
 (True,"Размер банды сравнён с 9.") (True,"Размер банды сравнён с 9.")
Пока всё нормально. Функция isBigGang принимает нормальное значение и возвращает значение с контекстом. Как мы только что увидели, передача ей нормального значения не составляет сложности. Теперь предположим, что у нас уже есть значение, у которого имеется журнальная запись, присоединен- ная к нему – такая как (3, "Небольшая банда.") – и мы хотим передать его функции isBigGang. Похоже, перед нами снова встаёт вопрос: если у нас есть функция, которая принимает нормальное значение и возвраща- ет значение с контекстом, как нам взять нормальное значение с кон- текстом и передать его функции? Исследуя монаду Maybe, мы создали функцию applyMaybe, кото- рая принимала значение типа Maybe a и функцию типа a –> Maybe b и передавала это значение Maybe a в функцию, даже если функция принимает нормальное значение типа a вместо Maybe a. Она делала это, следя за контекстом, имеющимся у значений типа Maybe a, ко- торый означает, что эти значения могут быть значениями с неус- пехом вычислений. Но внутри функции типа a –> Maybe b мы могли обрабатывать это значение как нормальное, потому что applyMaybe (которая позже стала функцией >>=) проверяла, являлось ли оно значением Nothing либо значением Just. В том же духе давайте создадим функцию, которая принимает значение с присоединенным журналом, то есть значением типа (a,String), и функцию типа a –> (b,String), и передаёт это значение в функцию. Мы назовём её applyLog. Однако поскольку значение типа (a,String) не несёт с собой контекст возможной неудачи, но несёт контекст добавочного значения журнала, функция applyLog
будет обеспечивать сохранность первоначального значения журна- ла, объединяя его со значением журнала, возвращаемого функцией. Вот реализация этой функции: applyLog:: (a,String) –> (a –> (b,String)) –> (b,String) applyLog (x,log) f = let (y,newLog) = f x in (y,log ++ newLog)
Когда у нас есть значение с контекстом и мы хотим передать его функции, то мы обычно пытаемся отделить фактическое значение от контекста, затем пытаемся применить функцию к этому значе- нию, а потом смотрим, сбережён ли контекст. В монаде Maybe мы проверяли, было ли значение равно Just x, и если было, мы брали это значение x и применяли к нему функцию. В данном случае очень просто определить фактическое значение, потому что мы имеем дело с парой, где один компонент является значением, а второй – журналом. Так что сначала мы просто берём значение, то есть x, и применяем к нему функцию f. Мы получаем пару (y,newLog), где y является новым результатом, а newLog – новым журналом. Но если мы вернули это в качестве результата, прежнее значение журна- ла не было бы включено в результат, так что мы возвращаем пару (y,log ++ newLog). Мы используем операцию конкатенации ++, что- бы добавить новый журнал к прежнему.
Вот функция applyLog в действии: ghci> (3, "Небольшая банда.") `applyLog` isBigGang (False,"Небольшая банда.Размер банды сравнён с 9.") ghci> (30, "Бешеный взвод.") `applyLog` isBigGang (True,"Бешеный взвод.Размер банды сравнён с 9.")
Результаты аналогичны предшествующим, только теперь коли- честву бандитов сопутствует журнал, который включен в оконча- тельный журнал.
Вот ещё несколько примеров использования applyLog: ghci> ("Тобин","Вне закона.") `applyLog` (\x –> (length x "Длина.")) (5,"Вне закона.Длина.")
ghci> ("Котопёс","Вне закона.") `applyLog` (\x –> (length x "Длина.")) (7,"Вне закона.Длина.") Смотрите, как внутри анонимной функции образец x является просто нормальной строкой, а не кортежем, и как функция applyLog заботится о добавлении записей журнала.
Моноиды приходят на помощь Убедитесь, что вы на данный момент знаете, что такое моноиды! Прямо сейчас функция applyLog принимает значения типа (a,String), но есть ли смысл в том, чтобы тип журнала был String? Он использует операцию ++ для добавления записей журнала – не будет ли это работать и в отношении любого типа списков, не толь- ко списка символов? Конечно же, будет! Мы можем пойти дальше
и изменить тип этой функции на следующий: applyLog:: (a,[c]) –> (a –> (b,[c])) –> (b,[c])
Теперь журнал является списком. Тип значений, содержащихся в списке, должен быть одинаковым как для изначального списка, так и для списка, который возвращает функция; в противном слу- чае мы не смогли бы использовать операцию ++ для «склеивания» их друг с другом.
Сработало бы это для строк байтов? Нет причины, по которой это не сработало бы! Однако тип, который у нас имеется, работа- ет только со списками. Похоже, что нам пришлось бы создать ещё одну функцию applyLog для строк байтов. Но подождите! И списки, и строки байтов являются моноидами. По существу, те и другие яв- ляются экземплярами класса типов Monoid, а это значит, что они ре- ализуют функцию mappend. Как для списков, так и для строк байтов функция mappend производит конкатенацию. Смотрите: ghci> [1,2,3] `mappend` [4,5,6] [1,2,3,4,5,6]
ghci> B.pack [99,104,105] `mappend` B.pack [104,117,97,104,117,97] Chunk "chi" (Chunk "huahua" Empty) Круто! Теперь наша функция applyLog может работать для любо- го моноида. Мы должны изменить тип, чтобы отразить это, а также реализацию, потому что следует заменить вызов операции ++ вызо- вом функции mappend:
applyLog:: (Monoid m) => (a,m) –> (a –> (b,m)) –> (b,m) applyLog (x,log) f = let (y,newLog) = f x
in (y,log `mappend` newLog) Поскольку сопутствующее значение теперь может быть любым моноидным значением, нам больше не нужно думать о кортеже как
о значении и журнале, но мы можем думать о нём как о значении с сопутствующим моноидным значением. Например, у нас может быть кортеж, в котором есть имя предмета и цена предмета в виде моноидного значения. Мы просто используем определение типа newtype Sum, чтобы быть уверенными, что цены добавляются, пока мы работаем с предметами. Вот функция, которая добавляет напи- ток к обеду какого-то ковбоя: import Data.Monoid
type Food = String type Price = Sum Int
addDrink:: Food –> (Food,Price) addDrink "бобы" = ("молоко", Sum 25)
addDrink "вяленое мясо" = ("виски", Sum 99) addDrink _ = ("пиво", Sum 30) Мы используем строки для представления продуктов и тип Int в обёртке типа newtype Sum для отслеживания того, сколько центов стоит тот или иной продукт. Просто напомню: выполнение фун- кции mappend для значений типа Sum возвращает сумму обёрнутых значений.
ghci> Sum 3 `mappend` Sum 9 Sum {getSum = 12} Функция addDrink довольно проста. Если мы едим бобы, она воз- вращает "молоко" вместе с Sum 25; таким образом, 25 центов завёрну- ты в конструктор Sum. Если мы едим вяленое мясо, то пьём виски, а если едим что-то другое – пьём пиво. Обычное применение этой функции к продукту сейчас было бы не слишком интересно, а вот использование функции applyLog для передачи продукта с указани- ем цены в саму функцию представляет интерес:
ghci> ("бобы", Sum 10) `applyLog` addDrink ("молоко",Sum {getSum = 35}) ghci> ("вяленое мясо", Sum 25) `applyLog` addDrink ("виски",Sum {getSum = 124})
ghci> ("собачатина", Sum 5) `applyLog` addDrink ("пиво",Sum {getSum = 35})
Молоко стоит 25 центов, но если мы заедаем его бобами за 10 центов, это обходится нам в 35 центов. Теперь ясно, почему при- соединенное значение не всегда должно быть журналом – оно мо- жет быть любым моноидным значением, и то, как эти два значения объединяются, зависит от моноида. Когда мы производили записи в журнал, они присоединялись в конец, но теперь происходит сло- жение чисел.
Поскольку значение, возвращаемое функцией addDrink, являет- ся кортежем типа (Food,Price), мы можем передать этот результат функции addDrink ещё раз, чтобы функция сообщила нам, какой напиток будет подан в сопровождение к блюду и сколько это нам будет стоить. Давайте попробуем: ghci> ("собачатина", Sum 5) `applyLog` addDrink `applyLog` addDrink ("пиво",Sum {getSum = 65})
Добавление напитка к какой-нибудь там собачатине вернёт пи- во и дополнительные 30 центов, то есть ("пиво", Sum 35). А если мы используем функцию applyLog для передачи этого результата функции addDrink, то получим ещё одно пиво, и результатом будет ("пиво", Sum 65).
Тип Writer Теперь, когда мы увидели, что значение с присоединенным моно- идом ведёт себя как монадическое значение, давайте исследуем экземпляр класса Monad для типов таких значений. Модуль Control. Monad.Writer экспортирует тип Writer w a со своим экземпляром класса Monad и некоторые полезные функции для работы со значе- ниями такого типа.
Прежде всего, давайте исследуем сам тип. Для присоединения моноида к значению нам достаточно поместить их в один кортеж. Тип Writer w a является просто обёрткой newtype для кортежа. Его определение несложно: newtype Writer w a = Writer { runWriter:: (a, w) }
Чтобы кортеж мог быть сделан экземпляром класса Monad и его тип был отделён от обычного кортежа, он обёрнут в newtype. Па- раметр типа a представляет тип значения, параметр типа w – тип присоединенного значения моноида.
Экземпля
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-17; просмотров: 199; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.17.137 (0.01 с.) |







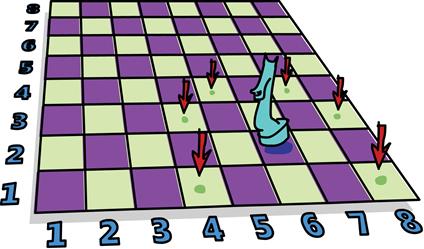 Есть проблема, которая очень подходит для решения с помощью недетерминированности. Скажем, у нас есть шахматная доска и на ней только одна фигура – конь. Мы хотим определить, может ли конь достигнуть определённой позиции в три хода. Будем исполь- зовать пару чисел для представления позиции коня на шахматной доске. Первое число будет определять столбец, в котором он нахо- дится, а второе число – строку.
Есть проблема, которая очень подходит для решения с помощью недетерминированности. Скажем, у нас есть шахматная доска и на ней только одна фигура – конь. Мы хотим определить, может ли конь достигнуть определённой позиции в три хода. Будем исполь- зовать пару чисел для представления позиции коня на шахматной доске. Первое число будет определять столбец, в котором он нахо- дится, а второе число – строку.

 Язык Haskell позволя- ет любому типу быть эк- земпляром любого класса типов, пока типы удаёт- ся проверить. Впрочем, он не может проверить, выполняются ли законы монад для типа, поэтому если мы создаём новый
Язык Haskell позволя- ет любому типу быть эк- земпляром любого класса типов, пока типы удаёт- ся проверить. Впрочем, он не может проверить, выполняются ли законы монад для типа, поэтому если мы создаём новый
 Мы познакомились с монадой Maybe и увидели, как она добавляет к значениям контекст возможного неуспеха в вычис- лениях. Мы узнали о списковой монаде и увидели, как легко она позволяет нам вносить недетерминированность в наши программы. Мы также научились рабо- тать в монаде IO даже до того, как вообще выяснили, что такое монада!
Мы познакомились с монадой Maybe и увидели, как она добавляет к значениям контекст возможного неуспеха в вычис- лениях. Мы узнали о списковой монаде и увидели, как легко она позволяет нам вносить недетерминированность в наши программы. Мы также научились рабо- тать в монаде IO даже до того, как вообще выяснили, что такое монада!



